IMF のキーパラメターは、
(1)下限 ml. 星にならない天体を含めない時は 0.08 0.1 Mo
(2)上限 mu. 通常 100 - 150 Mo
(3)特性質量mc. 勾配変化点。0.2 - 1 Mo.
(4)勾配パラメター。べき乗型か、対数正規分布かで変わるが。
勾配
勾配は次の式で定義される。
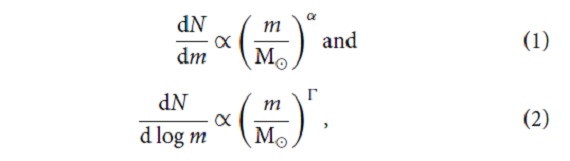
したがって、Γ = α + 1 である。サルピータ―の提案は α =-2.35 であった。
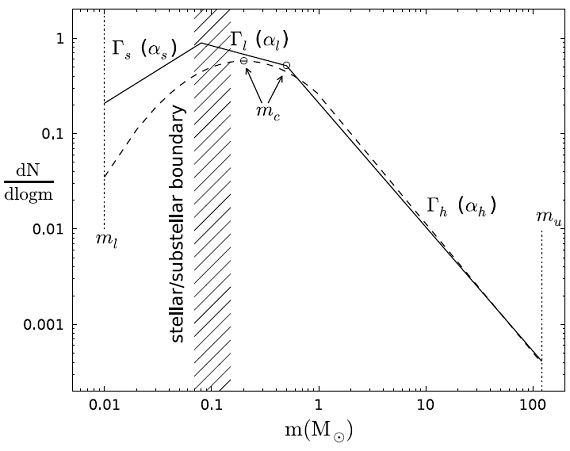
図1.IMF の図示。
| IMF を測る様々な方法を紹介し、比較する。 | 特にそれが普遍的であるかどうかに注意を払った。 |
|
キーパラメター IMF のキーパラメターは、 (1)下限 ml. 星にならない天体を含めない時は 0.08 0.1 Mo (2)上限 mu. 通常 100 - 150 Mo (3)特性質量mc. 勾配変化点。0.2 - 1 Mo. (4)勾配パラメター。べき乗型か、対数正規分布かで変わるが。 勾配 勾配は次の式で定義される。 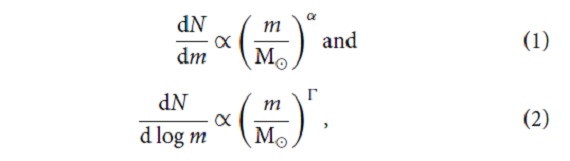 したがって、Γ = α + 1 である。サルピータ―の提案は α =-2.35 であった。 |
 図1.IMF の図示。 |
3.1.分解した星の計測と光度関数観測 IMF の問題点(1)光度から質量への変換に年齢とメタル量が必要。 (2)進化を終えた大質量星の補填 (3)連星の補正。 (4)星団における質量分離 普遍 IMF の有無 個々の観測から得られた IMF の差を観測誤差によるもので、普遍 IMF が 存在すると考える De Marchi et al 2010 と IMF 間の違いはリアルと考える Kroupa13 の解釈が対立している。 MW フィールド星の IMF 勾配 大雑把に言うと、MW フィールド星においては、高質量側 (M ≥ 0.7 Mo) ではサルピータより急な αh = -2.7, 低質量側では逆に平坦 な αh = -0.5 から -1 が得られている。 M ≤ 1 Mo の IMF に関しては多数の研究があり、 Chabrier03a や Jeffries12 にまとめられている。 |
しかし、 M = 1 - 10 Mo のフィールド星
に関しては殆ど観測がない。Bastien10 は MW SFH にある仮定をおいて、
αh = -2.65 を導いている。
SFH の影響 Elmergreen, Scalo 2006 は SFH = 一定と変化の二つの場合で、 IMF の推定 に影響することを示した。SFH が時間と共に低下している状況で SFH = 一定の 仮定で IMF を求めると、実際よりも急な勾配を導くことになる。彼らによると、 LMC/SMC での OB アソシエイションで Massey95, Massey02 が得た急勾配 αh = -5 (M = 25 - 100 Mo) はこの効果による。 M ≥ 1 Mo IMF の観測 M ≥ 1 Mo IMF の観測には OB アソシエイションや大質量の若い星団が用 いられる。Bastian10 を見よ。Offner14 は M = 3 - 10 Mo での 星団 IMF 勾配がサルピータ―の αh = -2.35 の周りに散ら ばることを見出した。 質量分離 星団星の質量分離は中心部に高質量星を集め、周辺部に低質量星を広げる効 果を持つので、狭い領域のサンプルを使うと IMF の推定に誤りをもたらす。 それを避けるには十分広い領域でサンプルを取る必要がある。 |
3.2.星団Zaritsky の ΥZaritsky12 は MW, Local Group 29星団の M/Lv 比 Υ を測った。 M は 速度分散から決めた。年齢差をなくすために、各星団が年齢 10 Gyr の時 に持つであろう M/Lv 比を単純な恒星モデルから計算した Υ*,10 を図2にプロットする。二つのグループに分かれて いることが見える。かれらはこれから次の結論を得た。 (1)log t ≤ 9.5 の若い星団は質量全体[0.1, 120] Mo でサルピータ型。 (2)古い星団は Kroupa93 型で低質量星の割合が低く、高質量での勾配が急。 (低質量勾配は小? ) 球状星団 球状星団の M ≤ 1 Mo 領域に関しては矛盾する結果が得られている。 Strader11 M31 の 200 球状星団に対する M/L 比を用い、 m < 1 Mo でα = [-1.3, -0.8] と平坦であり、低質量星が欠けている。 Zonoozi16 M31 の高メタル球状星団で M/L 比が小さいのはメタル量と共に高質量星の割合 が増加するためである。 van Dokkum, Conroy11 M31 の 4 球状星団の吸収線を測り、IMF が Kroupa01 と矛盾しない。 Goudfrooij, Kruijssen 2014 楕円銀河中の球状星団、特に高メタルでは、低質量星が過多である。M = [0.3, 0.8] で α = [-3, -2.3] が必要。 Zaritski14b 図2の星団で見た M/L は M/L 大が早期型銀河、 M/L 小が晩期型銀河に対応する。 それらは各タイプで、Gunawardhana11, vanDokkum12 が提案したような異なる IMF と合う。 最後の例は、恒星システムと銀河システムを観測から結びつける可能性を示す。 高質量限界 Calzetti10, Andrews13, 14 は水素電離放射光子数を測り星団内の高質量星 を調べた。Andrews14 は t <: 8 Myr と若く、500 Mo という低質量星団中にさえ 大質量星が存在することを示した。彼らは星団中の星質量はストカスティックに つまりランダムに分布していて、500 Mo 星団中に 120 Mo 星が現れることを許す と結論した。 (意味不明 ) それは Weidner14 の mu - Mcl 関係と対立する。 彼らの M 83 星団は [0.08, 120] Mo で Kroupa01 IMF と矛盾しない Hα/Mcl 比を持つと結論した。 |
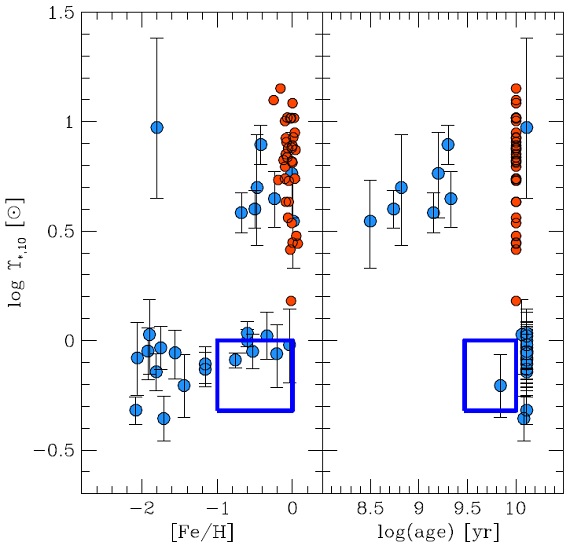 図2.Υ = M/L 比。青丸=星団。赤丸=早期型銀河。 青四角=円盤銀河。 (一点に他の色々なパラメターが 重なるから良い表示でない。 ) 星団 CMDs Weisz15 は M 31 内の若い中間質量星団 85 個の CMDs を研究し、 高質量側で勾配を αh = -2.45 +0.06 -0.03 で Kroupa01 の αh = -2.3 より少し急であることを見出した。 Veltchev04 は M31 SW 部の 51 OB アソシエイションの CMDs から αh = -2.59 を得ており、ほぼ一致する。 勾配の普遍性 Andrews14 も Weisz15 も彼らの結果は「普遍的」IMF と一致すると述べた。 彼らの主張は、星団星の IMF は全体としては MW IMF と同じだが、個々の 星団に関しては「変異」が生じているというものである。ストカスティシティ の重要性は Barker08 も指摘している。 Weisz15 の議論 Weisz15 は彼らの方法で MW で αh = -2.15±0.1, LMC で αh = -2.3±0.1 を得た。彼らは、m > 1 Mo では「普遍」勾配として彼らの αh = -2.45 を薦めている。 starburst cluster, super cluster starburst cluster, super cluster の観測は矛盾する結果を与えている。 M82 の super star cluster M82F で低質量星が欠けていることは Smith01, McCrady05, Bastian07 で確認されている。MW の nuclear star cluster を Lu13 が研究し、M = [1, 150] Mo での IMF 勾配 αh = -1.7 年齢 3.3 Myr を得ている。このほか色々あるが略す。 |
3.3.化学組成の観測[O/Fe] と IMF 勾配O、α元素 タイプII SNe Fe タイプ Ia, II SNe [O/Fe] が大質量星 IMF を探る手掛かりとなる。この比の高原部は タイプ II SNe のみでメタル化されているので、この比の値は IMF の高質量帯での傾きに影響される。Wyse, Gilmore 1992 によると、 M > 1 Mo での勾配を αh = -2.1 から -3.3 に変化さ せると、[O/Fe] を 0.4 dex 変えることになる。 (勾配が急になるとタイプ II SNe が 減って、初期 O 産出量が下がるのではないのか? ) Wyse98 はMW での[O/Fe] はサルピータ勾配と合うと述べている。 Mu Tsujimoto97 は元素組成の制限と M/L 比を結び付けて、M > 1 Mo で αh = [-2.6, -2.3] であり、かつ Mu = 50± 10 Mo とした。ただし、ここで述べられる Mu は物質を放出する星の 最大質量で、それより大質量でもブラックホールとなって反応生成元素を外に 出さない可能性はある。Gibson98 はイールドの不定性を考慮すると Mu には 30 - 200 Mo の巾があるとした。 |
dSphs Tsujimoto11 は dSphs で α 元素が少なく s-元素 (Ba) が多いことから、 Mu = 25 Mo とした。このアイデアは Weldner, Kroupa 2005 の、 低星形成活動環境では Mu が低いという意見と合う。 Portinari04a は MW 型 IMF は Sbc/Sc 銀河の M/L 比を説明するが、その場合 メタル量が高くなりすぎるので、 IMF 上限質量を下げる必要があるとした。ただ、 銀河風の効果を考えると微妙。 逆センスの主張 逆方向の極端な例として、Romano17 は、 CNO 同位体を追跡できるモデルで 星形成爆発銀河を研究した。彼らは αh = -1.95, つまり大 質量星の超過が必要であるとした。Sliwa17 も星形成爆発銀河 IRAS13120-5453 の CO 同位体比を説明するには大質量星超過が必要とした。 CEMPsと CMB CMB は星間ガスの最低温度を規定し、それは星形成の分裂片の特性長に影響 する。したがって、 CMB の時間変化は CEMP の比率に影響する。Tumlinson07 は Mc が高赤方変位になると増加しなければならないとした。 彼によると、IMF の時間変化を考慮しないと、次の誤りに陥る。 (1)IMF 一定の仮定で局所群中の銀河の CMD を解析すると早期の SFH を過小に 見積もる。 (2)UV のような高 z 銀河を観測すると逆に SFRsを過大に見積もる。 |
3.4. 種族 III 星IMF 進化種族 III 星は 100 Mo 以上と考えられている。低質量星は殆どか全くない。 最近、下限質量を下げる方向の研究が現れてきた。 Hirano14, Susa14. そのような星の IMF は MW 近傍のものと決定的に異なる。その意味では IMF は 進化する。ただそれは 「普遍性」とはちょっと意味が違う。「普遍性」は同時 期に存在する銀河間、または同一銀河内で異なるかどうかという問題であるから。 |
最電離 Bromm04 は種族 III 星による電離紫外光の放射、重元素生成の問題を強調した。 MW, ハローになぜ低メタル星が欠けているかの問題がある。 IMF Sobral15 は、「平坦または頭でっかち」IMF を z = 6.6 Lyα 系内の 種族 III 星に対し提唱した。一方 Bowler17 は IR 観測に基づき、その結論に 反対した。Fraser17 は極端低メタル星の化学組成からサルピータ勾配を支持し、 元素の SN 母星質量は最大 87 Mo で最低質量 Ml は SN より低い、 つまり 9 Mo 以下とした。 |
|
(1)局所群内では, IMF の高質量側勾配は αh = -2.5
の周り 0.3 以内に収まる。
(2)系外銀河球状星団では M/L 観測の結果から, 低質量側勾配は αl = [-3.0, -0.8] で MW 値の上だったり下だったり。 |
(3)星形成爆発のように活発な星形成活動の場では、IMF に変異があり、
Mc ≥ 1 Mo だったり、αh > -2.3
だったりする。
(4)dSphs のように低星形成環境では、Mu が低い必要がある。 |
|
CMF CMF =コアマス関数は IMF と似た形を持つ。違いは、折れ曲がり質量が 星に比べ 3 - 4 倍大きいことである。高質量側勾配は IMF と同じような 散らばりを示す。CMF と IMF との関係はまだ不明である。観測でどれが コアかを決め、その質量を導く手法はまだ統一されていず、同一データを 扱っても解析者で異なる結果になる。 |
PDF =確率分布関数 臨界柱密度 N(H2) = 1.4 1022 cm-2 は本当か? |
5.1.背景銀河のスペクトル合成スペクトル合成の力点は、合成カラー、 Mg b, Na D, TiO, CN である。 Whitford77 は Wing-Ford バンドが dwarf/giant 比の指標になり、古い種族 の IMF に制限を加えることを見出した。この手法は最近復活して、現在活発に 使われている。 Hα Kenneicutt83 は Hα の等値巾が高質量星の存在に鋭敏で、低質量星が 支配的な可視カラーと合わせると IMF の探索に使えることを示した。 Kenneicutt94 は近傍渦状銀河の IMF は高質量勾配が αh = [-2.5, -2.35] と Miller, Scalo79, Scalo86 が太陽 近傍で得た αh = [-3.3, -2.7] より平坦であることを示した。 |
彼らはこの違いの原因として、少なくとも部分的には、太陽近傍 IMF を作る際
のサンプル体積が大質量星が少ない箇所であったためとした。 Hα/UV 比 Hα/UV 比は Buat87 が提案した方法で、かれらは 31 晩期型銀河で M > 1.8 Mo 側勾配として αh = [-3.1, -2.3] を得た。 また別の手法 異なるタイプの銀河にはまた別の手法が考案され、使用されている。 UV 光度が現在星形成進行中の銀河に、 M/L 比や dwarf/giant 比が 星形成が停止中の銀河に適用される。 |
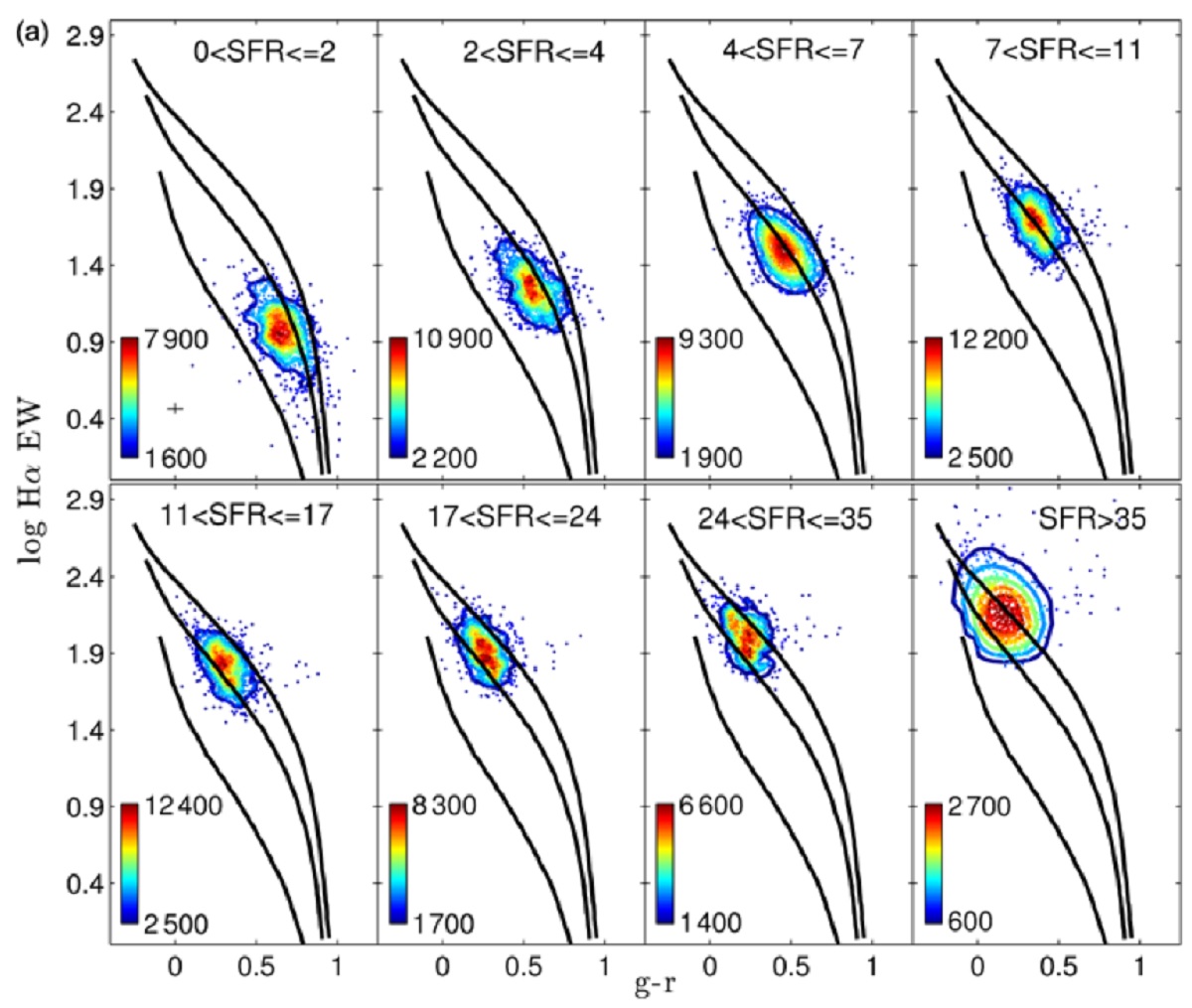
5.2.星形成銀河星形成が強いとαh 平坦星形成銀河は若い大質量星からの放射を使って診断される。 Hoversten08 は SDSS データを使い、Kennicutt94 の方法を拡大して、 サンプル銀河は全体として M > 0.5 Mo で αh = -2.45 の IMF と合致すると結論した。 αh が Mu と縮退するという保留付きながら、彼らは明るい銀河では αh = -2.4 で少し平坦になると述べている。 (0.05 の差!) ただし、星形成率が高い時に Mc が上がるという仮定でも似た結果がでる。 その場合、Mc = 10 Mo という非常に高い値になるが。 銀河系は αh -2.35 Gunawardhana11 は Galaxy and Mass Assembly survey データを用い、図3 の結果を得た。銀河系の星形成率だと αh -2.35 となる。 13C/12C Zhang18 は4つの星形成爆発銀河で CO 観測を行い、13C/12C が低いことを見出した。彼らはそれを大質量星の割合が高いことに起因すると見做した。 |
結論 他に色々考えて、Meurer09 は次の結論に達した。 (1)観測を説明するのは IMF の高質量星端の変動である。 (2)Mu = 30 - 120 Mo で変わり得る。 (3)M = [0.1, 100] Mo で α = [-3.3, -1.3] という考えもあり得る。 |
|
対象銀河による差 星形成銀河では高質量側の IMF に研究が集中し、passive galaxy では 逆に IMF の低質量端が関心の的となっている・ その結果を定性的に述べると、 (1)星形成が盛んな銀河では M > 0.5 Mo で αh が平坦 である。 (2)passive 銀河では M < 1 Mo で αl が急峻になる。 |
矛盾なのか、どうか? passive 銀河では低質量星の超過が見られ、星形成銀河では大質量星の超過 が観測される。これは一見矛盾に見えるが、そうなのか?過去に星形成を経験した 巨大楕円銀河中心部の当時の環境と、現在星形成が盛んな銀河の環境とで IMF が 異なると考えるなら、矛盾はない。そうなのか? |
|
SFH/SMD Lilly96 と Madau96 の重要な研究以来、宇宙の luminosity density と それに伴う SFH の観測は精度を上げてきた。それは大規模銀河サーベイによる SMD = stellar mass density の測定 Cole01 で補足されてきた。 この二つの宇宙規模のセンサスは IMF に対し基本的な境界条件を与える。 他には、系外銀河背景放射とコア崩落超新星率もある。これらは、ある宇宙年齢 での全銀河サンプルにより IMF のテストとなる。 放射密度 「普遍」IMF はそれらの「全」宇宙観測量と合致するだろうか?全銀河を用いると SFH が平滑化されるので、個々の銀河より系統誤差が減らせる。 SFH 観測は大質量星からの UV や FIR の放射密度に基づき、SMD 測定は低質量星 からの可視、近赤外の放射密度に基づく。 IMF が違うとその二つの種族の星の 割合が変わり、それに伴って放射密度が変わる。Cole01 のような研究初期でさえ、 SFH と SMD の二つを「普遍」IMF と両立させるためにはダスト量が驚くほど少な い必要があることが認識されていた。 |
「普遍」IMF の矛盾 「普遍」IMF の矛盾点は、 (1)「普遍」としてもサルピータ (M=[0.1,100]Mo でα=-2.35) でない。 MW の低質量側ではより平坦(Kroupa01, Chabrier03b) だし、SFH から導かれる SMD は高すぎる Madau, Dickinson14 からである。 (2)「普遍」としてもMW 型 (低質量でαl=-1.3, 高質量で αh<-2.35) でない。 SFH から導かれる SMD は高すぎる Hopkins06 からである。 (3)「普遍」としてもMW 型 (低質量でαl=-1.3, 高質量で αh>-2.35) でもない。 MW ではサルピータ勾配 Kroup01 だからである。 (4)M31 の高質量側勾配の高精度測定は αh = -2.45 を 与えている。「普遍」としてもサルピータでない。 そのように、様々な勾配が与えられるので IMF は「普遍」ではない。 |
|
|
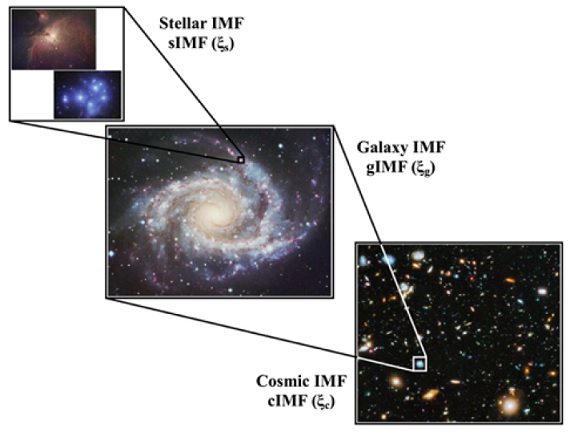 図7.IMF が「普遍」的でないならば、対象に応じて異なる IMF を考える 必要がある。sIMF = 星団規模、gIMF=銀河規模、cIMF=宇宙規模という風に。 |
9.1.観測は何を語るのか? |
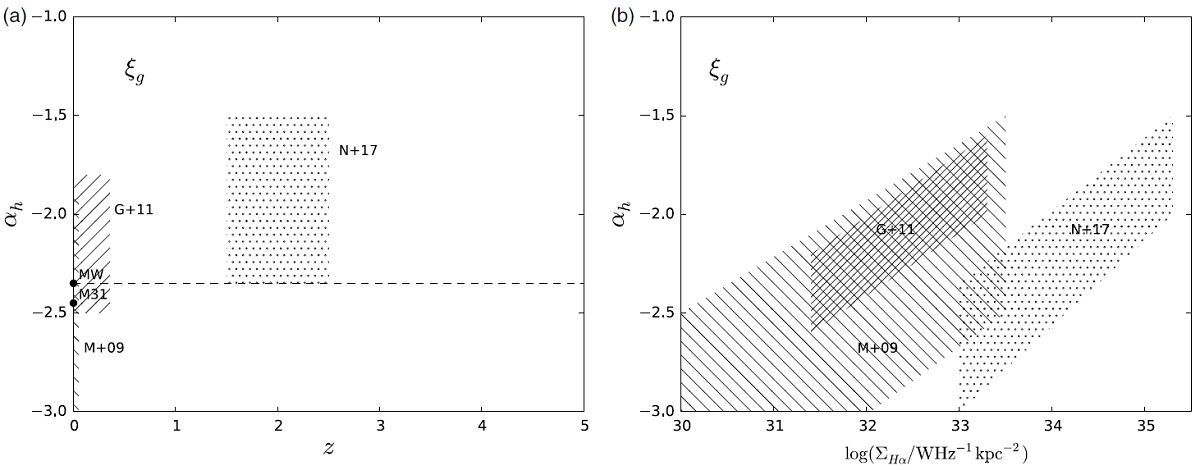
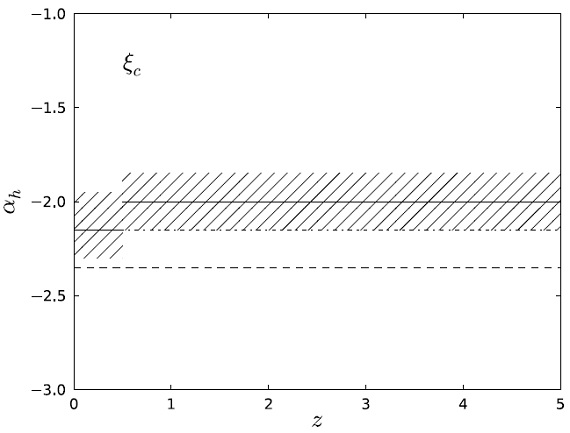 図8.実線+斜線部:Wilkins08b による宇宙 IMF &gzi;c に対する αh の可能な変化。 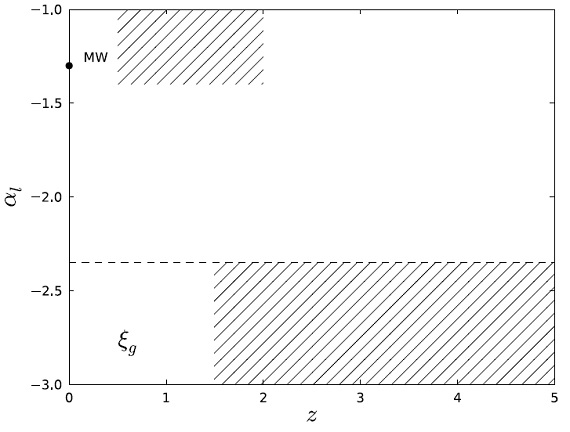 図10.低質量側での勾配 αl と赤方変位=星の形成時期 の指標との関係。MW=Kroupa01. 上部斜線=Bastian10 による MW t = [5, 10] Gyr の値。下斜線=passive 銀河 t = [9.5, 12.3] Gyr の勾配。 |

|
|
|

|
|
|

|
|
|
