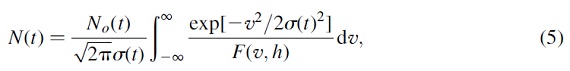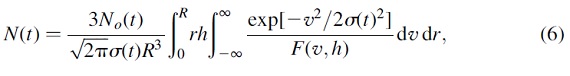The Recent Star Formation History of the Hipparcos Solar Neighbourhood

　アブストラクト　

　１．イントロダクション　

　２．方法　

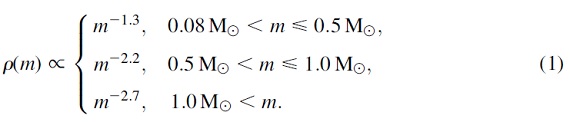
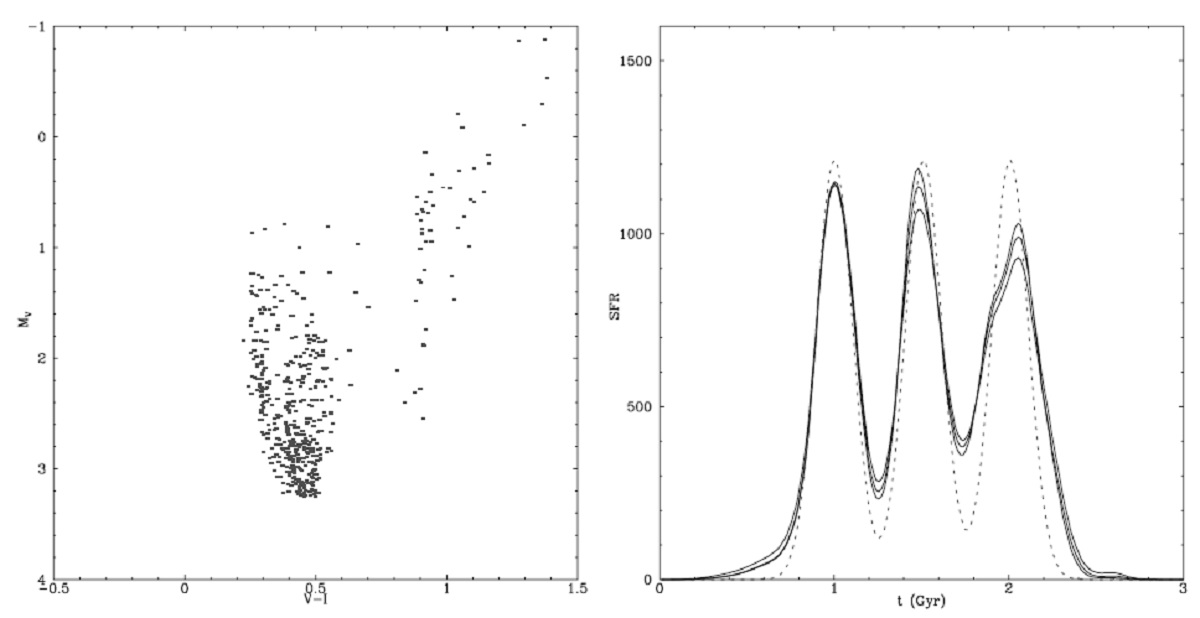
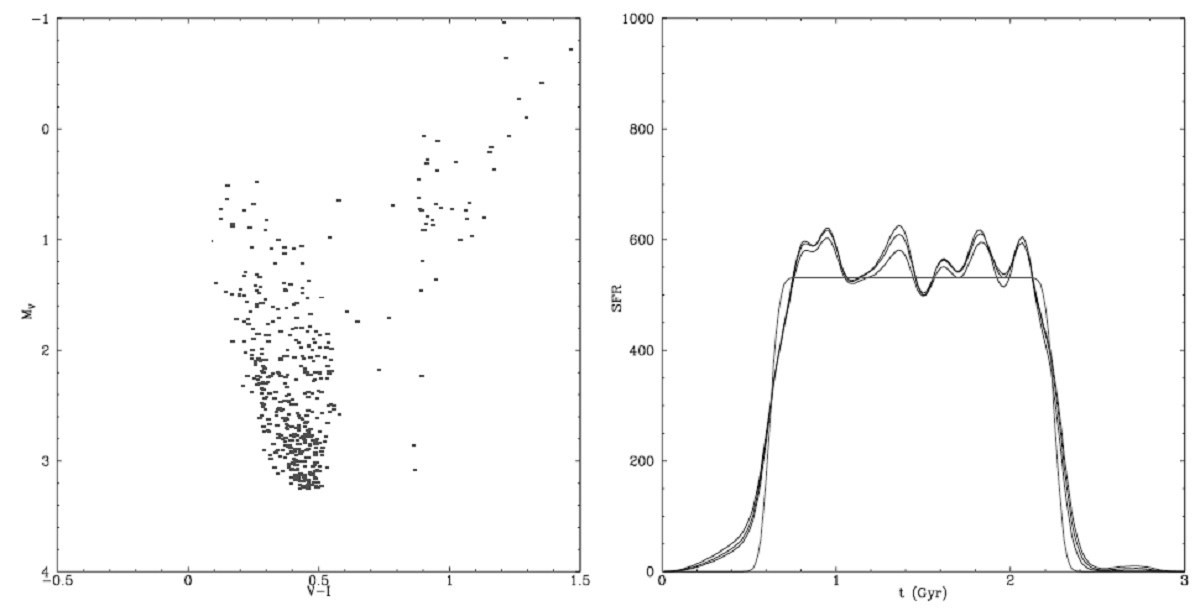
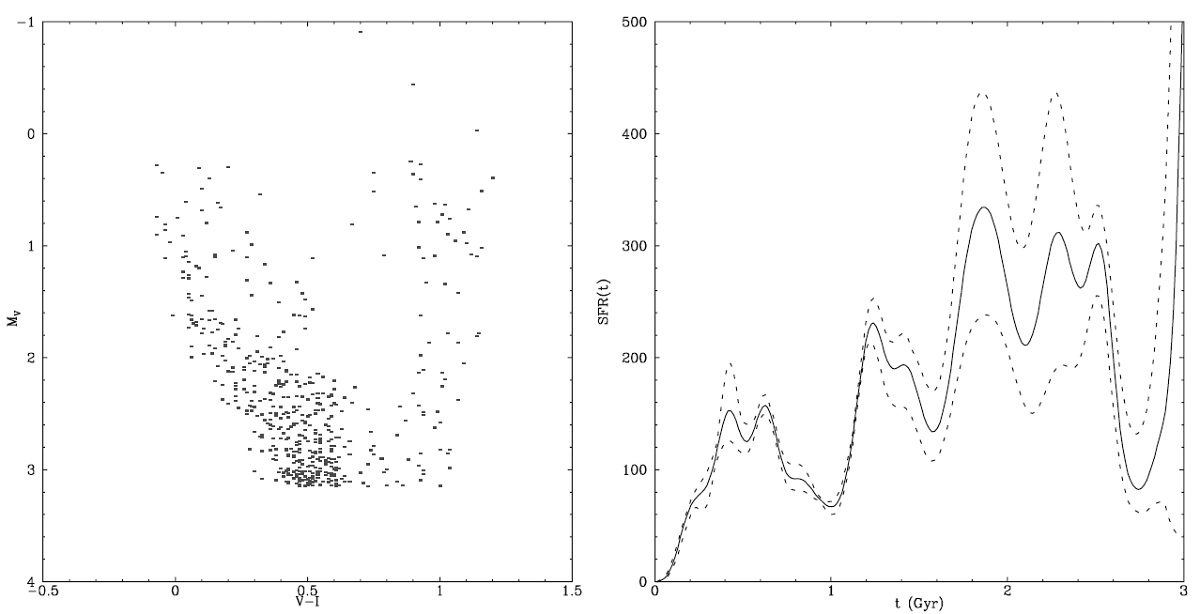
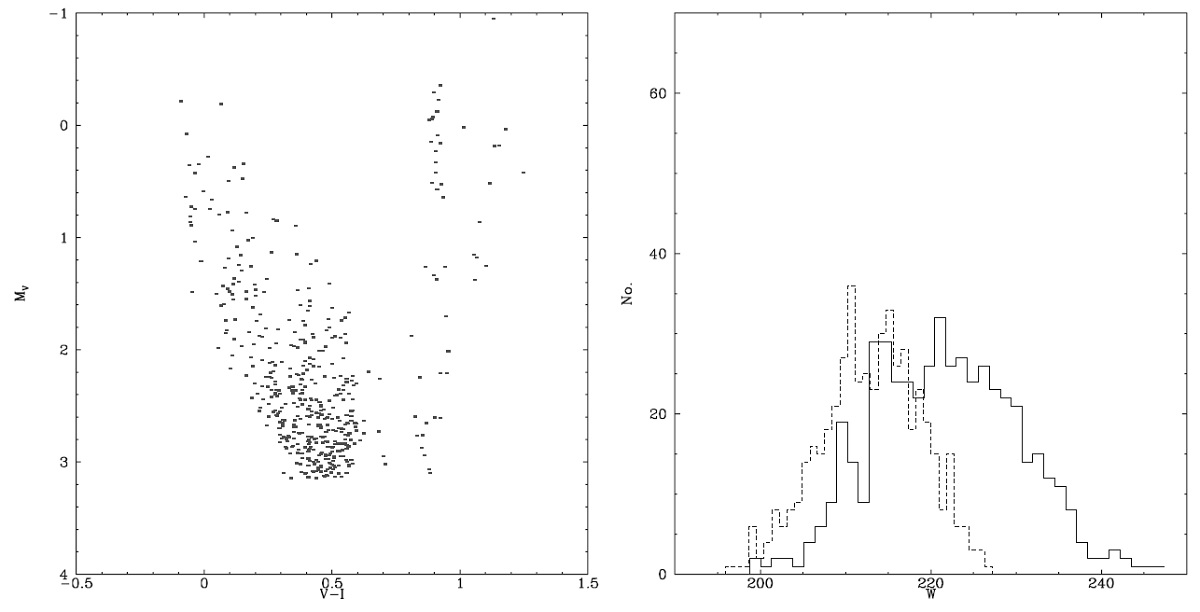
IMF　 　IMF は結果にあまり影響しない。我々は以下の IMF を使う。 これは Kroupa, Tout, Gilmore 1993 の銀極方向と太陽近傍にフィットした 式である。 　メタル量と恒星進化モデル　 　太陽近傍のヒッパルコス星を扱うので、 [Fe/H] = 0 を仮定する。 星の進化モデルには Fagotto et al 1994, Girardi et al 1994 のパドヴァ等 時線を採用する。モデル HR-図を CMD に変換するには Lejeune, Cuisinier, Buser 1997 の変換式を使う。我々が扱う範囲では　Weiss, Salaris 1999 が 述べているような 巨星、ＡＧＢ星で起きる Bessell, Castelli, Plez 1998 の 最新の変換式との狂いは起きない。 　カラーと光度　 　我々が入力するのは、n 観測星のカラー ci と光度 li である。ある SFR(t) から n サンプル星が生じる確率を計算 する。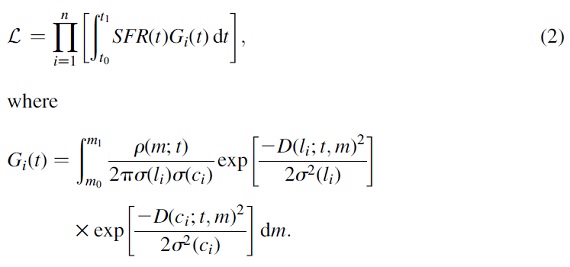 ここに、ρ(m;t) は年令 t の等時線に沿った、質量 m の星位置での点密度であり、 仮定した IMF と m の星のその位置での滞留時間で決まる量である。 σ(li), σ(ci) は i-星の観測エラーである。D(li;t,m) と D(ci;t,m) は i-星の観測 (li, ci) と 一般的な質量 m, 年齢 t の星 (l, c) との間の距離である。この先、 Gi(t) を尤度マトリクスと呼ぶ。 (「ρ(m;t) は年令 t の等時線に 沿っての」は式でどう表現されるのか？(m,t) 毎に (l,c) 面上での確率分布を 想定する。等時線上の質量 m 星の位置を中心にしたガウス分布を考えるのだろ うか？それとも、その位置に滞在時間に比例した重みを与え、 ) Hernandez et al 1999 でも同様の式が導入されている。しかし、そっちでは 観測エラーしか考慮されていない。これは対象が dSph だからである。式(2) は Tolstoy, Saha 1996 の式の拡張版である。

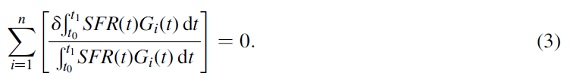
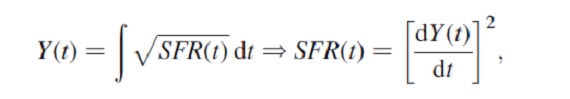
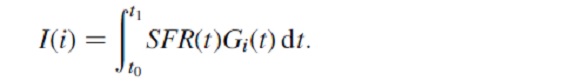
微分積分方程式への変換　 　L(SFR) が極値をとるという条件は 　　　δL(SFR) = 0 と表現される。この式を変分法で扱う。まず、 式 (2) の i に関する積の変分 を取り、その結果の和を L で割って、次式を得る。 新しく次の量 Y(t) を導入する。 そして、この式を上の式 (3) に入れると、オイラー方程式として次を得る。 ここに、 である。こうして極値を与える関数を求める問題が、式 (4) のような微分積分 方程式へと変わった。この式を境界条件 SFR(t1) = 0 で解く。 (この境界条件の意味は何か？ ) 　解法の詳細　 　解法の詳細は Hernandez et al 1999 にある。そこでは式の導出もより詳し く述べてある。また、解のテストも行い、満足な結果が得られた。式 (4) の解 には極値だけでなく、全ての停留点が含まれる。したがって、HR 図による確認が 重要である。 　変分法の利点　 　この方法が優れている点は、 （１）パラメターを使用しない。 （２）繰り返し近似のような長時間計算が要らない。

　２．１．二つのテスト　

　３．サンプル選択と結果　

限界等級　 　ヒッパルコスカタログの限界等級はスペクトル型と銀緯に依存する。 G5 より 早期の星に対しては、 　　 Vlim ＝ 7.9 + 1.1 sin|b| で与えられるが、混乱を避けるためここでは Vlim = 7.9 とする。 　完全サンプル　 　図３には距離エラー 20 % 以下で mV < 7.9 のヒッパルコス サンプルの Mv - d 関係を示す。実線は体積制限サンプルの一例で、Mv < 3.15, m < 7.25 で完全である。シミュレイションの結果、SFR(ｔ）を安全 に決められるのは 3 Gyr であることが分かった。これから、式(2) において、 t0 = 0, t1 = 3 Gyr となる。式を解くために、分解能 15 Myr の等時線を 200 本使用した。 　赤色巨星の排除　 　赤色巨星のターンオフ等級は限界等級より暗い。赤色巨星の 混入を排除するため、サンプルは V - I = 0.7 より青い星に限定した。 　古い星の補償（？）　 　年齢が経つにつれ、形成された星の内で観測 CMD に居残れる星の割合は低下 して行く。その結果、 CMD を反転して得た SFR(t) の古い部分は過小に評価さ れる。 (「低下」は SN や WD で　CMD から 消えていく過程を意味するのか？それなら当たり前のことで、「過小評価」 の原因になるとは思えない。理解できない。 ) これは仮定される IMF とRGB チップの星質量で与えられる補正項により補償される。 (これも理解できない。 )

図３．ヒッパルコスカタログ中、距離エラー 20 % 以下の星の距離 d と絶対 等級 Mv の関係。鋭い下輪郭は完全性限界が mV = 7.9 にあるこ とを示す。直線区画＝今回の体積限界サンプル（Mv<3.15)。曲線＝ mV = 7.25 の完全性限界。この値でのエラーは図１，２ での 値とほぼ同じになる。 　解の分解能　 　IMF, メタル量、 CMD 上での観測星の位置が与えられると、尤度マトリックス Gi(t) が計算できる。これのみが反転法に必要な入力情報である。体積限界 サンプルの星数が 450 と小さいため、SFR(t) の小さな構造は数個の変動でし かなくなる。また、時間分解能も 50 Myr となるが、それでもこれまでの研究 よりずっと高い。

　３．１．運動学および幾何学の補正　

運動学的補正　 　F(v,h) = 銀河面垂直速度 v の星が銀河面高度 [-h, h] に滞在する時間の 割り合い、N(t) = 年齢 t の星の数、No(t) = 観測された年齢 t の星の数、 σ(t) = 速度分散。すると、 距離限界サンプルの空間領域は球形なので、幾何学的補正も必要となる。 ここに、 R = サンプル領域半径、 r = 太陽からの距離(動径座標)、h2 = R2 - r2. F(v,h) の評価には銀河面垂直方向の力の法則が必要である。Kuijken, Gilmore 1989 はこれが調和振動ポテンシャルから大きく外れることを示した。 我々はこのポテンシャルから F(v,h) を求めた。σ(t) = 20 km/s とした。

銀河面への投影量　 　こうして、垂直方向速度分布をガウシャンと仮定し、観測される No(t) は N(t) へと変換される。これは銀河面への投影量である。 　SFR(ｔ）　 　我々の場合、この方法で与えられた SFR(t) が　No(t) に取って代わる。 方程式 (6) が最終的な SFH を与える。それが Mo Myr-1 kpc-2 単位の SFR(t) を与えるのである。

　３．２．結果　

図４　 　図４左：ヒッパルコス距離エラー 20 % 以下で、 mV < 7.25 の Mv < 3.15 で完全な体積制限サンプルの CMD。右：反転法で得た結果。点線は 幾つかの異なる Mv 限界からの再現である。全て同様の結果を与える。 　SFR(t)　 　SFR(t) には、ある程度の一定 SFR(t) が見られ、それに重なって、強い約 0.5 Gyr 間隔の準周期的な成分が見える。 t = 3 Gyr 付近の鋭いピークは第 ５サイクルの開始が境界条件 ＳFR(３)＝０のため丸められた結果かも知れない。 　彩層活動　 　我々の結果は時間分解能が高すぎて、以前の研究と比べることが困難である。 Rocha-Pinto et al 2000 は彩層活動の研究から SFR(t) を出した。我々の結果は t = 0.5 と > 2 Gyr では同じ結果である。しかし、 t = 1 - 2 Gyr での 低下はない。

擬周期性の解釈　 　擬周期性の可能な解釈の一つは密度波の通過である。もっとも単純なモデル (Binney, Tremaine 1987) によれば、太陽付近で、パターン回転速度 Σp はそこでの回転速度 Σ の２倍である。 通過間隔は次の式で与えられる。 ここに、 m = 腕の数。Ωp = 0.5 Ω = 14.5 km/s/kpc である。 (Ωp はΩの倍じゃなかっ たのか？) m = 1 で SFR(t) のピークを説明するには十分であろう。ただ、最近の研究は もっと大きな Ωp = 23 - 24 km/s/kpc を示す。この場合、 m = 2, 4 腕モデルが 0,5 Gyr 間隔と整合する。 (Ωp が大きくなったら m = 0.7 とかにしないといけないんじゃないのか？ 　 ) 　別解釈　 　別解釈として、もし太陽が共回転位置に近いなら、バーは SF の引き金に なるかも知れない。その場合、バーのパターン速度が 40 km/s/kpc が必要。 また分子雲衝突でも自己励起振動があり得る。

　４．結果のテスト　

　５．結論