アブストラクト赤外スペクトルの分類ISO SWS により、ダストのない星の 2.38 - 45.2 μm, R = 400 の スペクトルを撮った。この観測は赤外スペクトルの分類法を向上させる 計画の一部である。特に、Kraemer et al 2002 の 1.N - 1.NO 天体 (O- リッチのダストシェルなしの通常星)の詳細な分析に向いている。 連続光 連続光は Engelke 関数 (Engelke 1992) でフィットされた。この連続光 から決めた恒星角直径は他の方法による値とよく合った。 吸収線等値幅 CO, SiO, H2O 吸収線等値幅の解析は、それらから、熱い B, A, F 型星を冷たい星から区別できる事を示した。等値幅間の相関が強い事も 判った。 |
1.イントロ近赤外分類Smith-Lambert 1985, Origlia et al 1993, Andrillat et al 1995, Morris et al 1996, Wallace,Hinkle 1996,Meyer et al 1998 IRAS LRS 分類 Sloan,Price 1998 SWS 分類 SWS 2.38-45.2 μm. Kraemer et al 2002 広範なスペクトル。 2.36−4.1, R=1500 Vandenbussche et al. 1999, 2002 本論文はR=400でダストのない星を扱う。モデルはDucin 2000.。 M5+は流体力学効果の注意がいる。 |

|
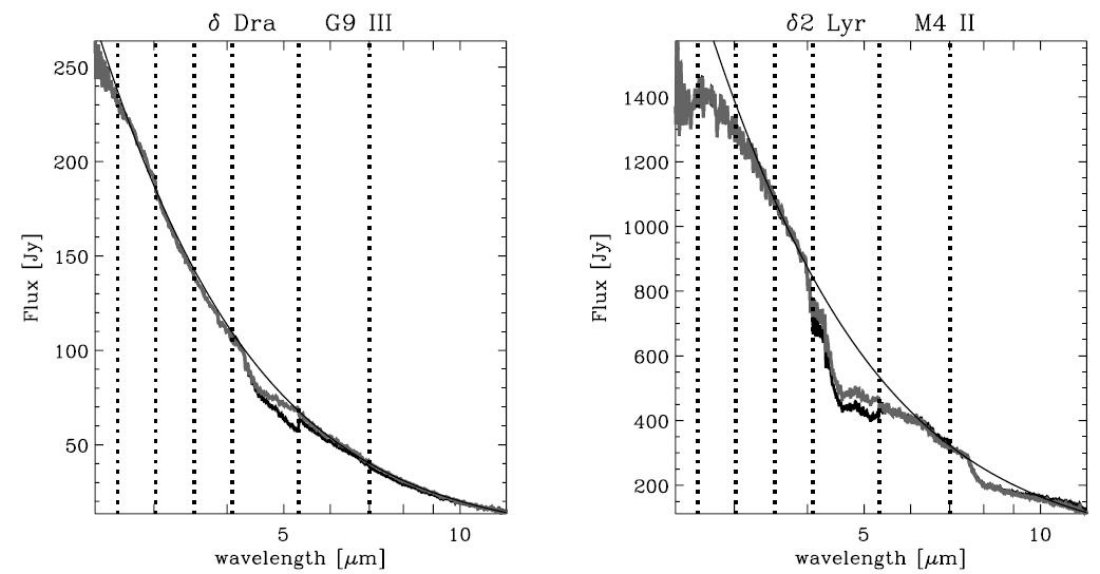
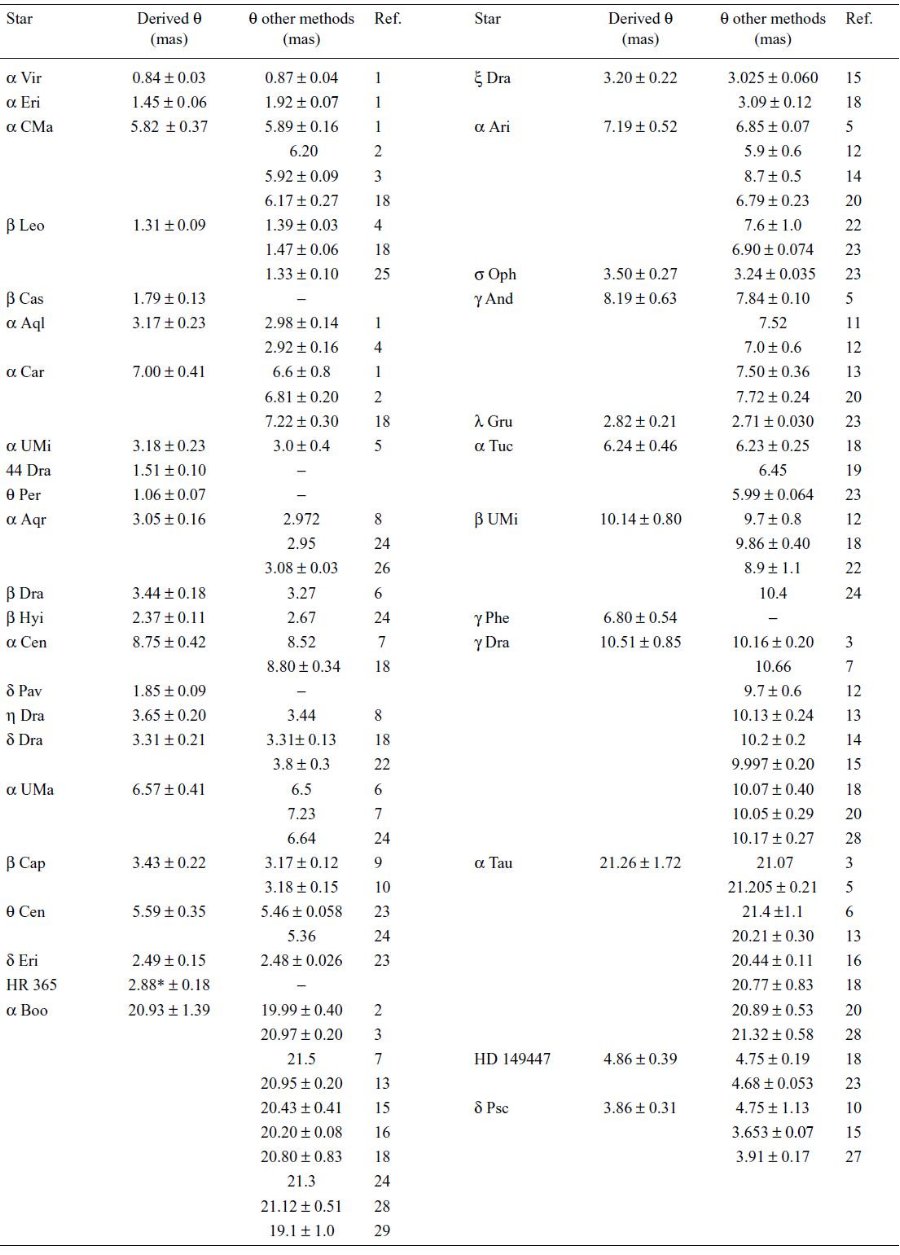
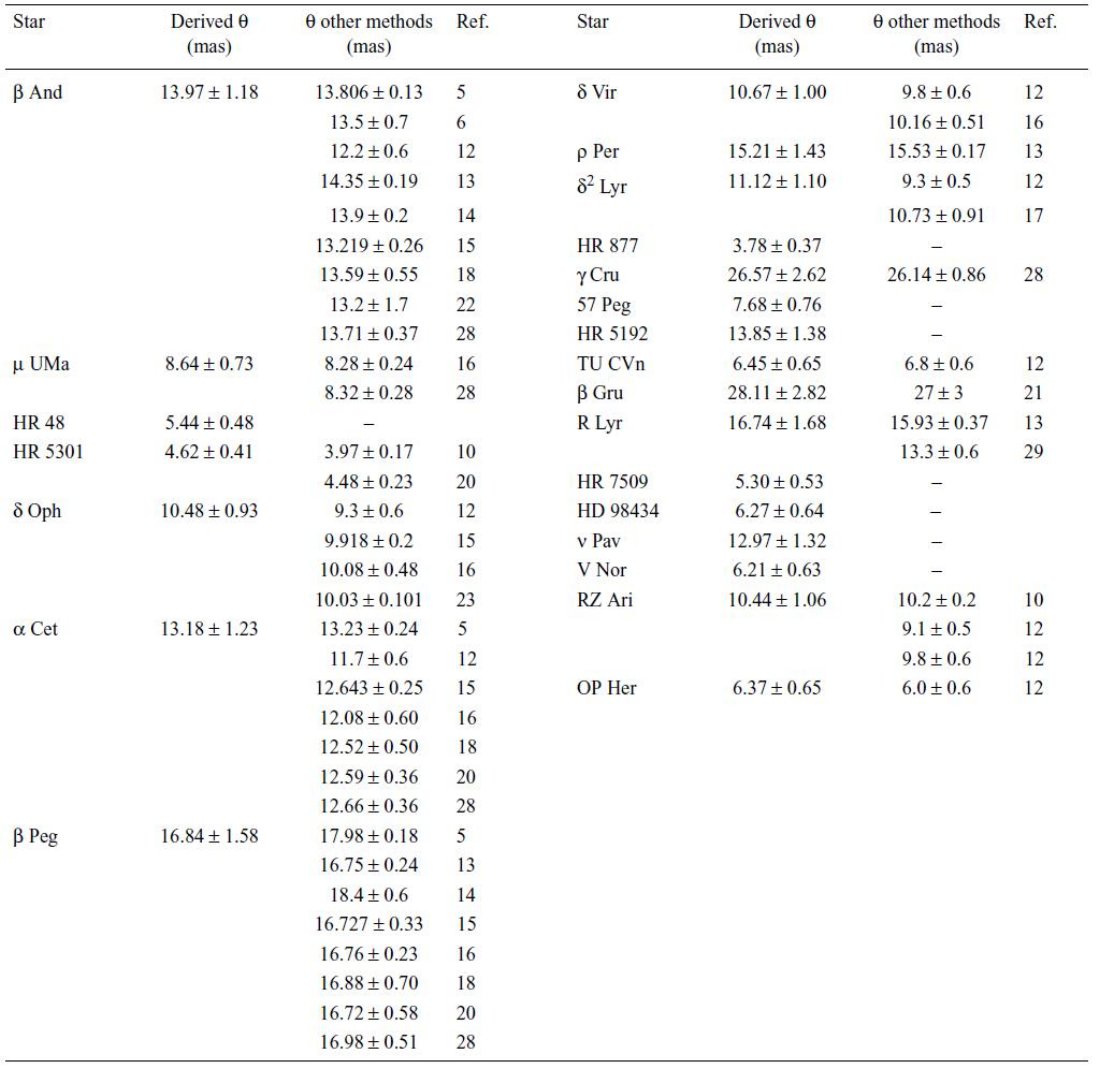
対象星の条件 (1)MIRにダスト徴候見えず (2)B−M型 (3)S/Nが高い (4)R=1000−200 2.1.連続光Engelke 関数Engelke1992 でフィット 標準星との比較で、λ<20μでは±3%、 λ>20μで±5%の精度 Engelke関数と観測スペクトルとのフィットは(1)式の Ωのみをフリーパラメターとして行った。 有効温度 TeffはMK分類のTeff を使用した。下の表の通りである。理由はAOTバンド境界の不連続が 余りに大きな誤差を生み出すからである。 異なった温度スケールが採用されているが、相互には誤差範囲内で一致している。 Refの著者達が見出した一つは、K4.5型で光度クラス I は 光度クラス III より400K低いということである。 吸収帯 Engelke関数は吸収帯の寄与を含まない。そこではフィットは当然悪い。 そこで、2.38−2.9μ、4−10μでの フィットの重みは下げた。さらに、水の吸収でM型星の連続光が下がっている可能性がある。そこで、M0−M4型 スペクトル(Teff=3878−3595K)を0.02、M5−M6スペクトル(Teff=3470−3380K)を0.05下げてから フィットした。 星の角直径 クロスチェックとしてフィットから求めた星の角直径を観測値と比べた(表3)。 一致はかなりよい。  表2 スペクトル型とTeff Refは論文参照。 |
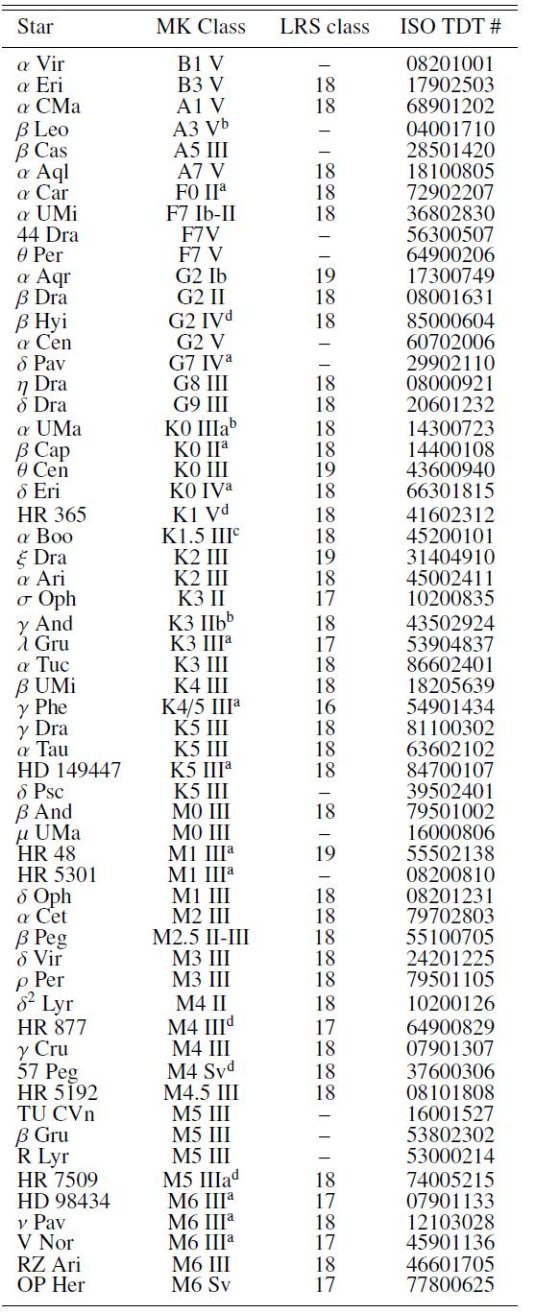 表1 MKクラスはJaschek(1978)より。 |
|
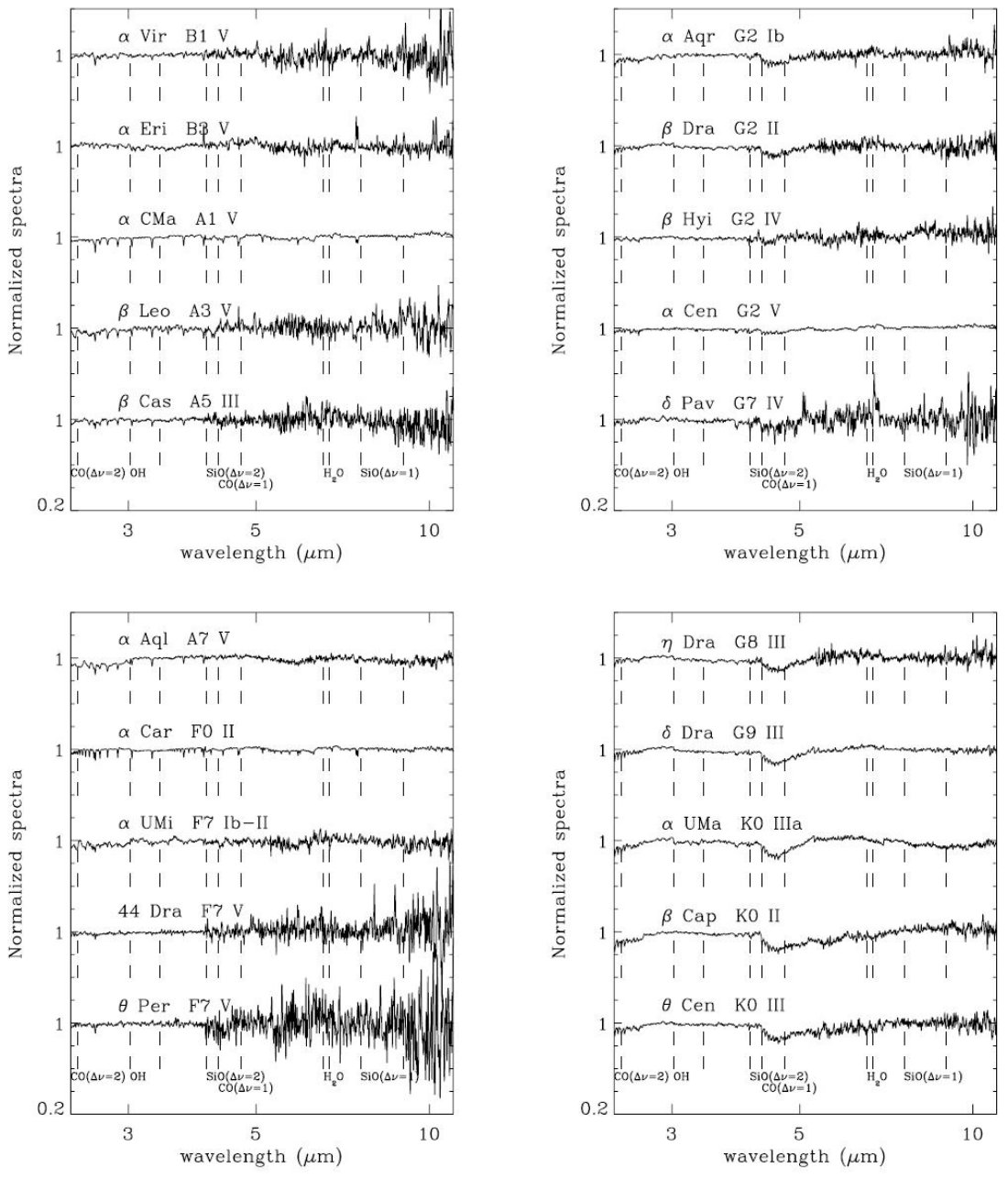
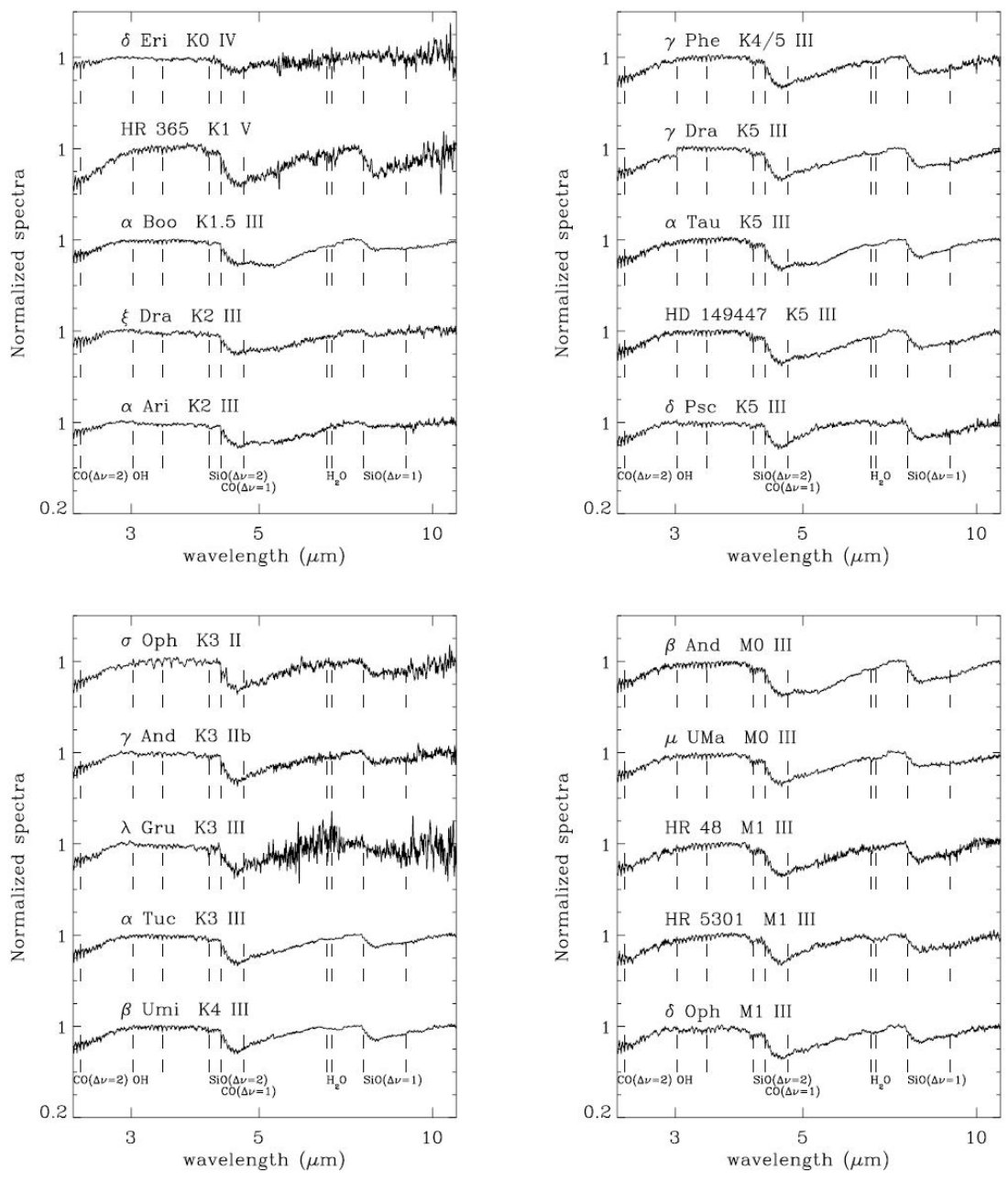
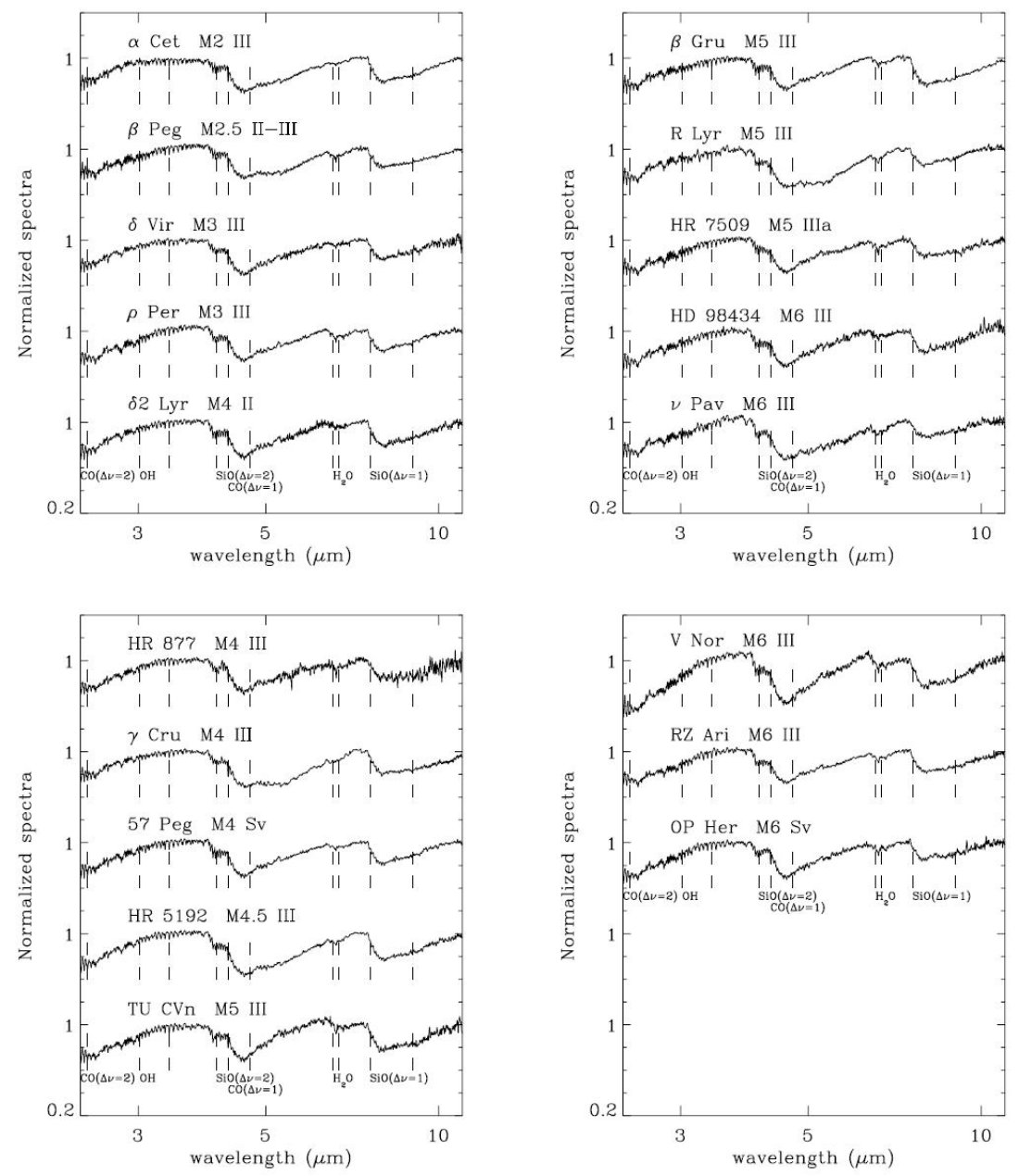
規格化スペクトルの表示 図2−4はAOT端の不連続を補正した規格化スペクトルを示す。 スペクトルの特徴 B,A, F型ではH,Heラインが支配的。 G型 原子線。COの4.6,2.5μが見え始める。 K型 OHバンド(3−3.56μ)、 K0でSiO1stovertone(4μ)とfundamental (8μ)見え始める。 Ari(K2III)、βAnd(MoIII),δOph(M1III) 幅広の水のν2ベンディングモードが6.4−7μに見える。 M2+ これが一般的な特徴になる。 特に6.55−6.7μが強く、分類に使える。 LRS との対照 ISOではLRS分類を前進させることを目指している。 ここではLRS blueクラス16−19のfeatureless |
新しい分類法 Kraemer のISO分類では1.N、1.NOが対象になる。 新しい提案は、 (1)強いH線、 (2)強いCO吸収。SiOなし。 (3)強いCO+SiO (4)強いCO,SiO+H2Oベンディング 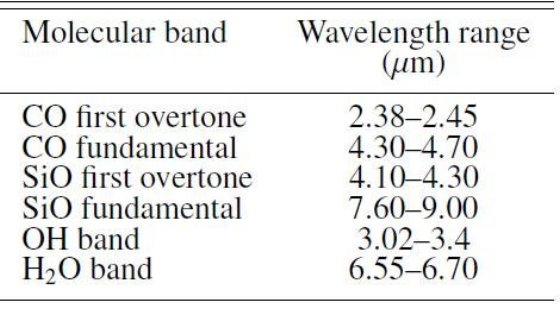 表4.分子バンドの波長範囲 |
3.1.分子等値幅とMKクラスバンド巾の設定表4第2列のバンド幅は他のバンドとの重なりを最小にするように決め られていて、真のバンド幅とは異なる。 特に水バンドは2.38−12μに広がっていて、表4の範囲を超えて いる。 バンド吸収による等級変化 前節に述べたように、この準連続吸収的なバンドはその波長帯で M0−M4星では2%、M5−M6星で5%連続光を下げると仮定して Engelksフィットを行った。 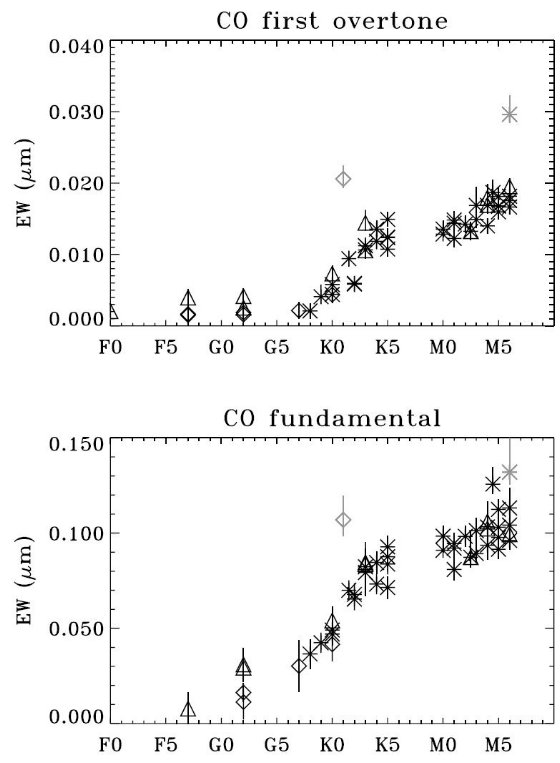 図5.CO第1倍音と基底振動吸収の等値幅 △: 光度クラス I, II、*: III、◇:IV, V K型ではM型より勾配が急である。M型で緩くなることはOriglia82も指摘している。 |
OH と H2O OHはK0型で既に見える。しかしM型にならないと強度は大きくならない。 H2Oの存在は確認できるが、温度依存のはっきりした傾向は確立できなかった。 図5,6から判る事 図5と図6から何が言えるだろうか? B,A,F型星は原子線の相対比と分子バンドが存在しないことで区別できる。 G型は弱いCO第1倍音と基底振動が存在し、SiOがないことで分かるが サブタイプまでは分からない。 CO と SiO (K0−K2),(K3−M3),(M4−M6)はCOとSiOの強度で区別される。 波長6μでの水はM2+で出てくるので、(K3−M3)を分割できる。 HR365(K1 V)とVNor(M6 III)は少し変。 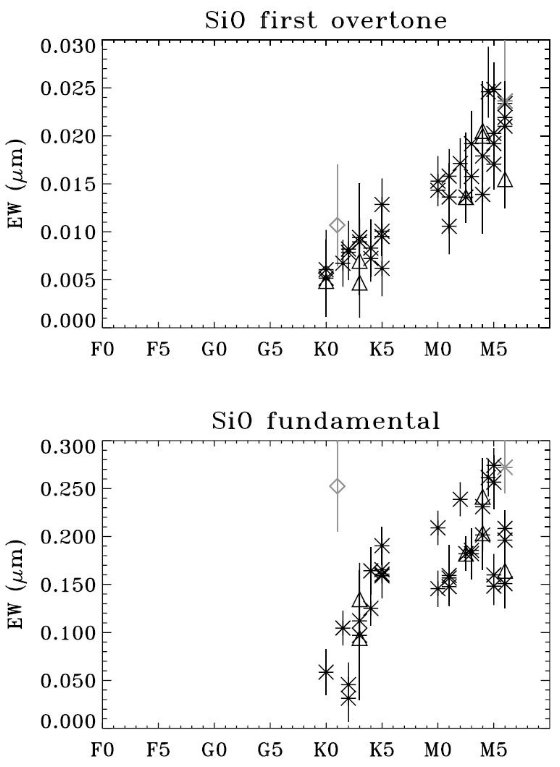 図6.SiO第1倍音と基底振動吸収の等値幅 △: 光度クラス I, II、*: III、◇:IV, V 第1倍音がK型ではM型より勾配が緩い。 Rinsland,Wing1982に指摘。 基底振動では、一般的にKからMへと強くなっていくがあまり明瞭ではない。 動力学的効果などが温度効果を打ち消すのであろう。 |
|
モデルの予測と観測の不一致 大気モデル: SiO第1倍音はTeffが下がると強くなる。 観測: Cohen,Davis1995 SiO基底振動を KAO, UKIRT でK,M型について観測。 初めはリニアに増加するが、K5 III - M0 III でピーク。 その先は一定。 筆者たち 以前、SiO基底等値幅が晩期 K, M0 - M3, M6が で同じくらい。 Sloan,Price 1998 AGB星でSiO基底吸収の深さがK5の9%からM6の15% 程度の変化。モデルとの不一致はおそらく晩期になると重力 が弱くなり、その効果が温度を打ち消すのであろう。 |
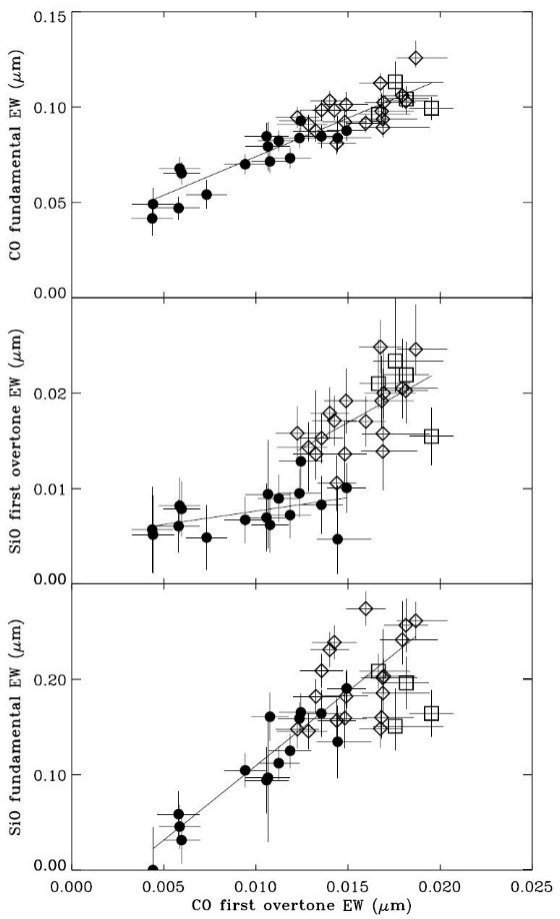 図7 CO基準に対する他バンド ●: K型、 ◇: M0−M5型、 □: M6型 上段はCO第1倍音で、KからMまで相関は良い。 中段はSiO第1倍音で、K型とM型とで異なる系列をなす。 下段はSiO基準振動でM5までは相関がよいが、M6は異なるふるまい。 こうして、地上で得られるCO第1倍音の結果とスペクトル型から他のバンド の様子が推定される。 |