|
T Tau 分布に集団が実在 数種の統計手法を用いて、Taurus-Airiga 分子雲内の前駆主系列星の非乱雑配置の性質を 導いた。0.3° スケールで指数 -1.2 のべき乗型二点角度相関関数が観測分布をよく 再現することがわかった。これは T Tau 分布に集団が実在することを意味する。 Taurus で単独星の形成は生じない また、最近接距離分布からは投影間隔の中間値が 0.3 pc であることが判った。この間隔は 分子雲コアのサイズ(∼0.1 pc)より少し大きいだけである。これは Taurus のような 低密度星形成領域では孤立した単独星の形成は生じないことを示す。 |
近接した星形成は一般的 狼座、カメレオン T1, ヘビツカイ座 ρ 星、オリオン、 NGC700/IC5070, NGC2264 領域の最近接距離分布からも似た性質が得られた。我々の解析は終局的には孤立星 となる場合でも通常は比較的近接して生まれることを示す。細長く伸びた分子雲コア内部での 多重性の星形成がそのような結果をもたらす機構を提供している。 星集団を 6 個見出した 牡牛座に投影半径 0.5 - 1 pc の統計的に有意な星集団を 6 個見出した。これらの小集団は 夫々が 15 個程度の星を含み、分子雲全体に分布している。集団間の内部運動は 0.5 - 1 km/s で ある。 |
|
最近の牡牛座-御者座 T Tau 星探査 牡牛座領域には 140 の T Tau 星が知られている。うち 41 個は最近（表１）の探査で 発見された。 1986 年以来、可視前駆主系列星の数は 41 % しか増えていない。今や、 V ≤ 15.5 では検出はほぼ完全と言える。Briceno et al 1993 は対物プリズムサーベイで 12 個の前駆主系列星を発見したが、 V = 15.5 より明るいのは一つしかない。 WTTS は分子雲の外まで Walter et al 1988 は牡牛座領域近傍には約千の WTTS が存在すると予想した。しかし それらは 400 平方度に渡り広がっているだろう。一方、12CO から知られる 分子雲の広がりは 100 平方度である。 TTS はあまり動けない。 TTS は ≤ 2 km/s の速度分散しか持たず、想定されるその寿命 1 Myr の間には生まれた場所からあまり動けない。従って TTS の空間分布は 低質量星がどう生まれたかの研究に役立つ。 |
 表１．最近の牡牛座サーベイ |
２．１．牡牛座 - 御者座分子雲種族可視前駆主系列星Herbig-Bell カタログ (1988, HBC) は、可視前駆主系列星を 集めている。我々は α = [3h45m, 5h05m], δ = [16°45', 30°45'] の TTS を考える。HBC にその後のデータ から増減して、139 個の可視前駆主系列星サンプルを得た。 |
IRAS サンプル サンプルの第２グループは IRAS PSC から得た。Kenyon et al 1993 によると F(25), F(60) > 0.5 Jy ではほぼ完全な探査が 得られている。クラス I 天体は前駆主系列天体全体の約 10 % を 占めている。 |
２．２．相関関数 W(θ)２点相関関数の定義
ここに、Np(θ) は、分離角 = [θ-Δθ/2, θ+Δθ/2] のサンプル中のペアの数。 Nr(θ) は、サンプルと同じ数の天体を乱雑にばら まいた時に生ずる平均ペアの数。 相関関数の近似式 図２は牡牛座の 121 前駆主系列星に対する２点相関関数 である。ビンの巾は対数で 0.4 である。これを次の式で近似した。 W(θ) = A θB ここに、 B = -1.22 ±0.24 である。これは、牡牛座の TTS が乱雑に分布しているのではなく、雲内に閉じ込められていることを 示す。 |
 図２．牡牛座前駆主系列星の 2 点相関関数。領域は図１の 破線枠。 |
２．３．最近接距離サンプル域の制限サンプル域は図１の破線枠に限定した。乱雑分布の中間値 0.35 ″ は実際の TTS 分布のそれより約３倍大きい。 つまり、TTS は互いに集まっているのである。 |
 図４．実線＝ TTS 最近接距離の分布。一点破線＝ランダムモデル。 点線＝中間値 |
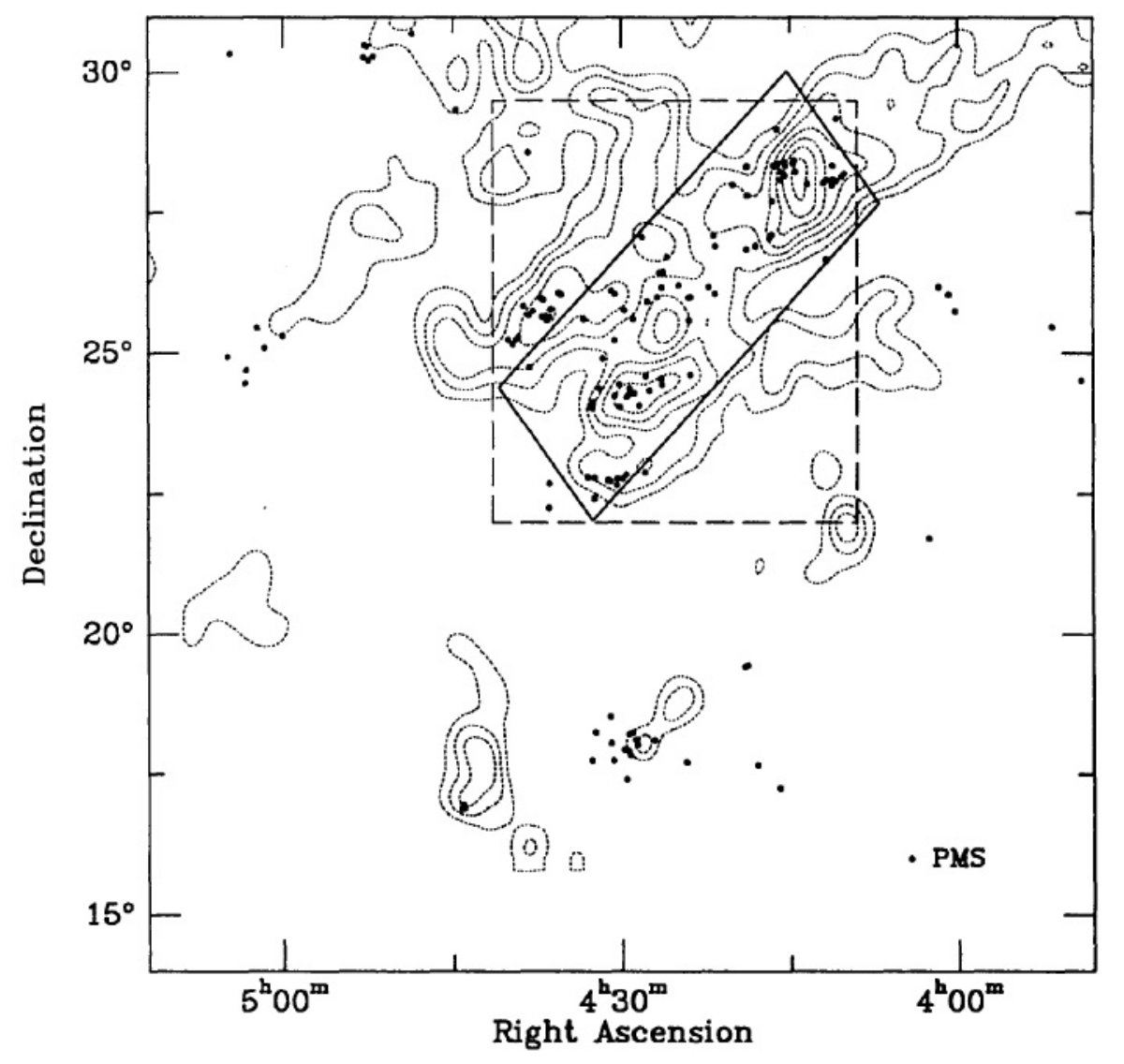
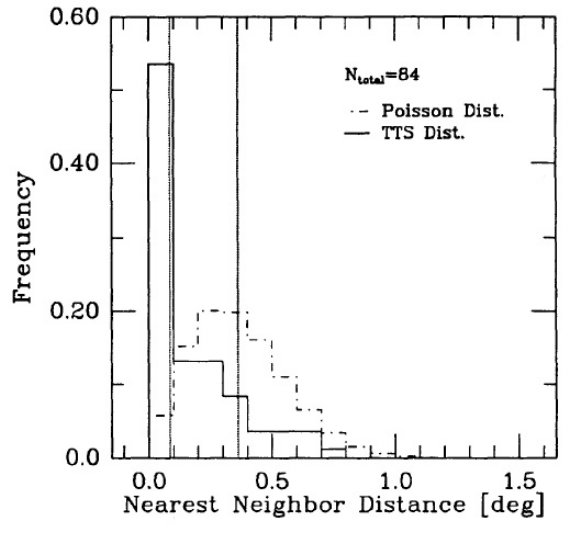
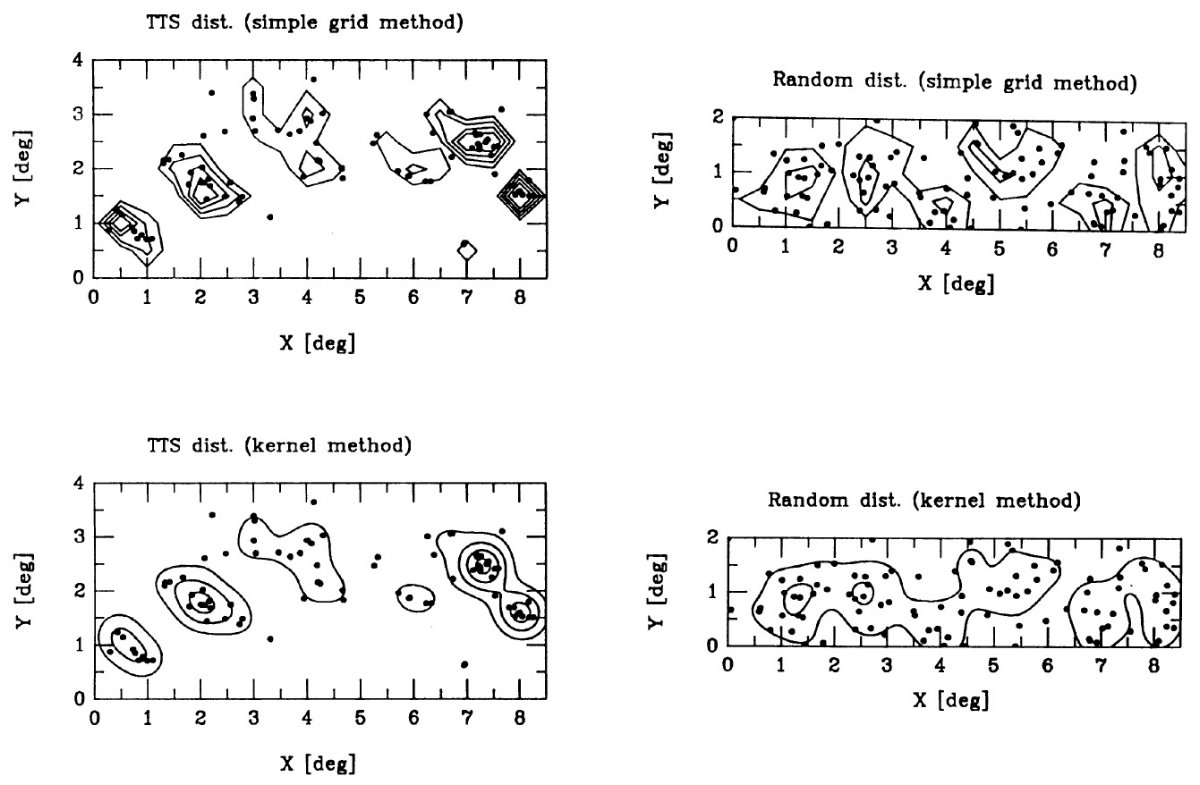
３．１．単純グリッド法グリッド区画図１破線域 34 平方度内には前駆主系列星が 97 個ある。 この領域を 0.5×0.5 deg2 で分割し、 17×8 グリッド区画を作り、各区画内の星を数える。 等密度線 次に、線形内挿で等密度線を描いた結果が図７左上である。 右上は、ファクター２小さい領域に同じ数の星を乱雑分布 させてつくった等密度線である。なぜなら、実際の前駆主系列星 は有効面積が約半分の帯状領域内にあるからである。 有意な集団の境界値 乱雑分布でできた等高線の最も高い値、ここでは 10 deg-2 、 を有意な集団の境界値と考える。すると、 図７左上から、(X, Y) = (6, 2.2), (4, 2.5) グループは 除去される。 ３．２．カーネル法カーネル法の定義カーネル法(Silverman 1986) は密度分布が滑らかになる 利点がある。それは以下の式で定義される。
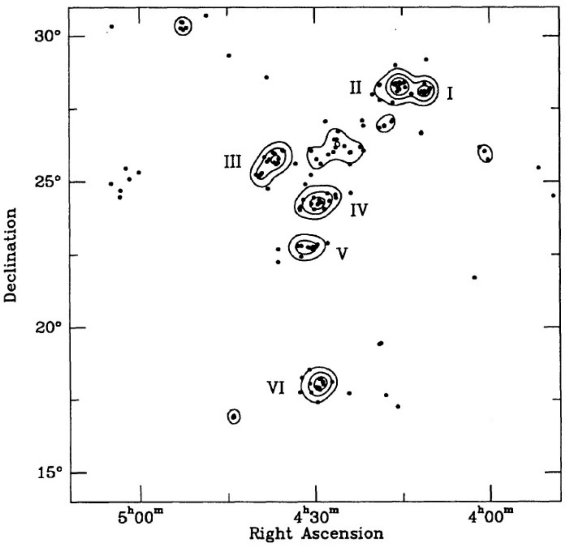
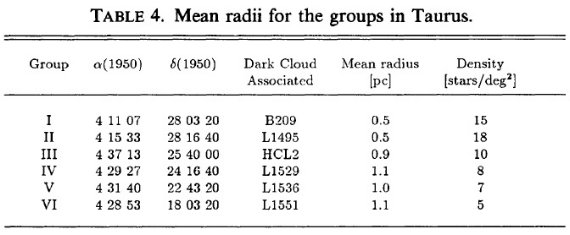
r2 = (δ-δi)2+ (α-αi)2 cos2δ つまり、各サンプル点がガウシャンで広がっていると考えるわけである。 図７の左下、右下はカーネル法で作った等密度線を描いた。さらに 牡牛座全域でカーネル法を用いて等密度線を描いた。この領域には 172 の前駆主系列星が存在する。図８はその結果である。 図７で見出した集団の外側にさらに二つの集団が加わった。 集団に属する星 大体半数 78/152 が集団に属する。残りは全域に渡って広がっている。 連星系や多重星系の個々の星を個別に数えると、 116/172 = 70 % の星が 集団に属し、残り 30 % が孤立していると言える。 半径 表４には星集団の中心位置と半径を載せた。 |
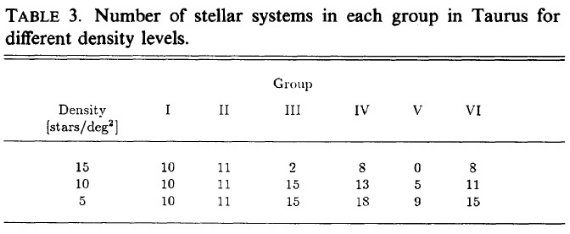
 図８．平滑化パラメタ―0.3° を使用した牡牛座全域の等高線図。高さは 5, 10, 15, 20 星/deg2. ローマ数字は牡牛座のグループ。  表３．牡牛座の前駆主系列星集団、３つの等密度線の 内側の星の数。  表４．牡牛座の前駆主系列星集団の平均半径 |