The Intrinsic Colours of Stars and Two-Colour Reddening Lines

　アブストラクト

　１．イントロ　

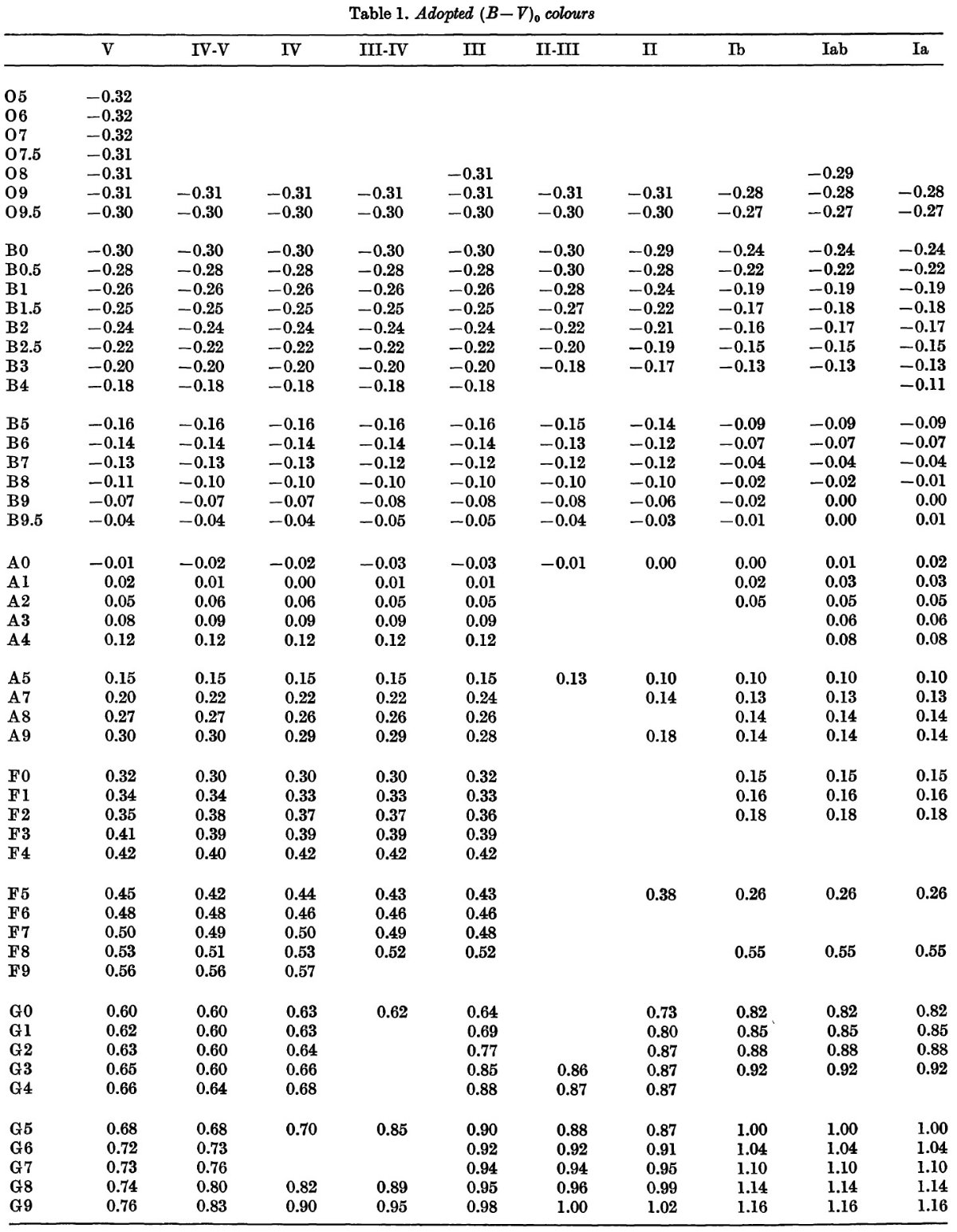
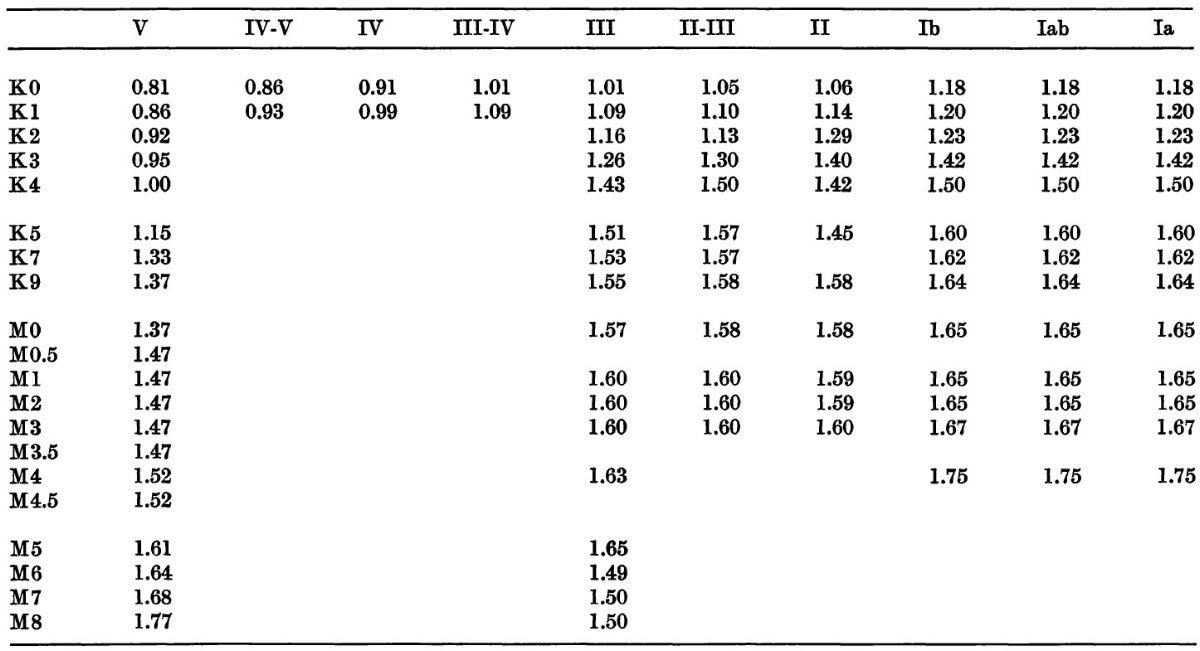
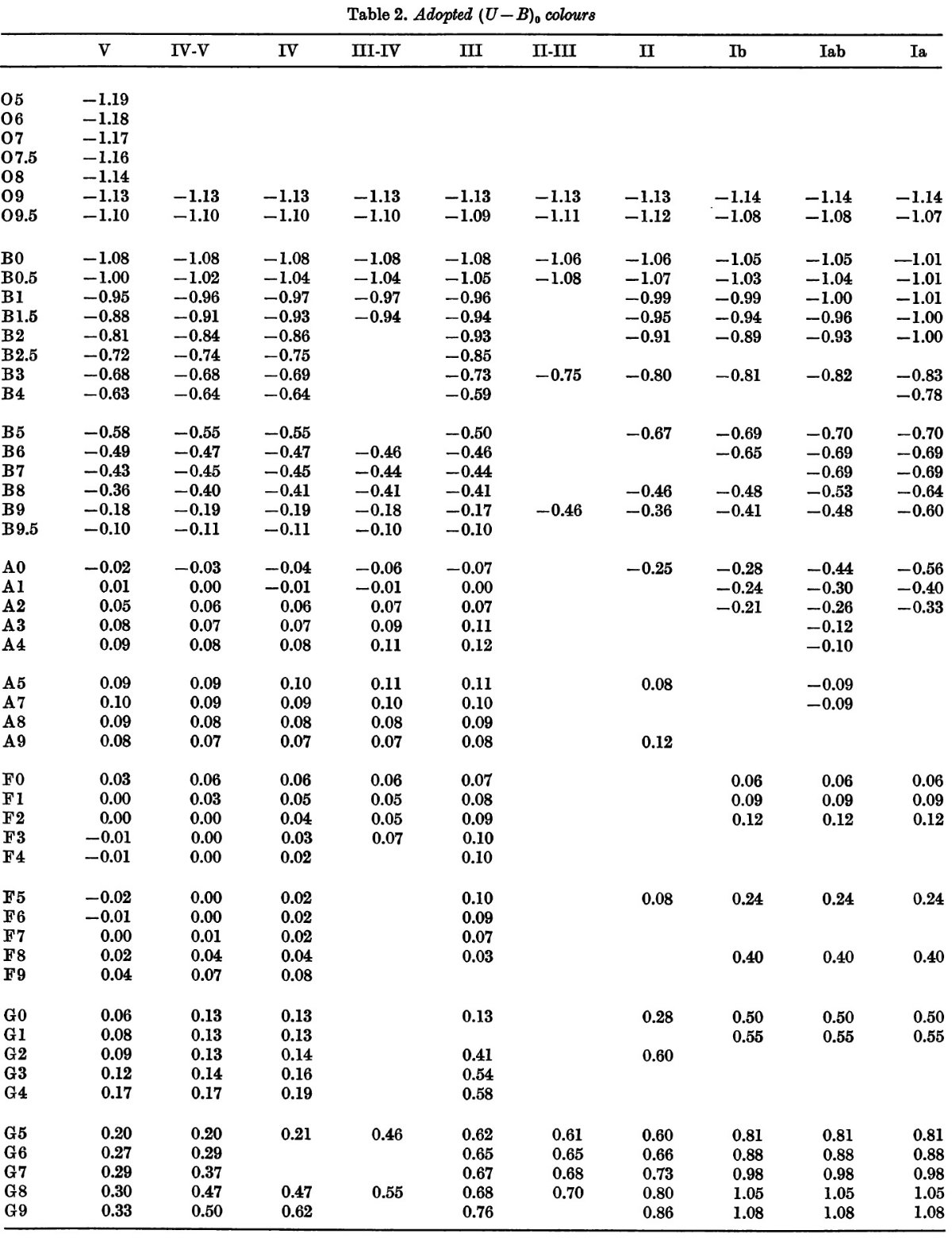
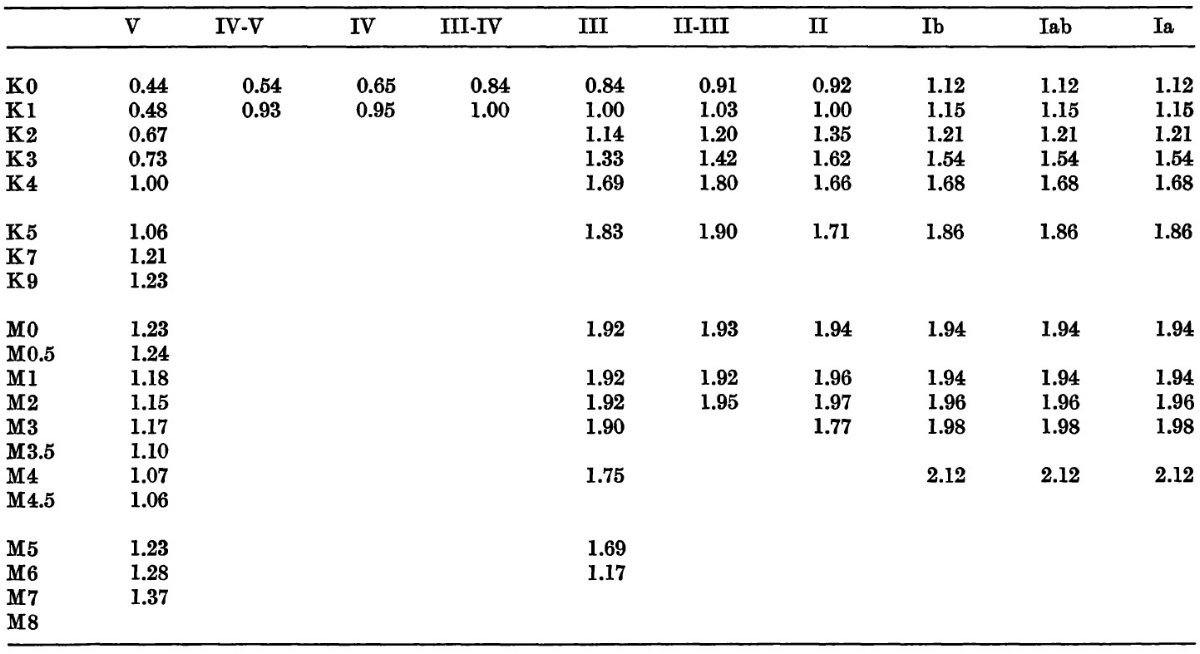
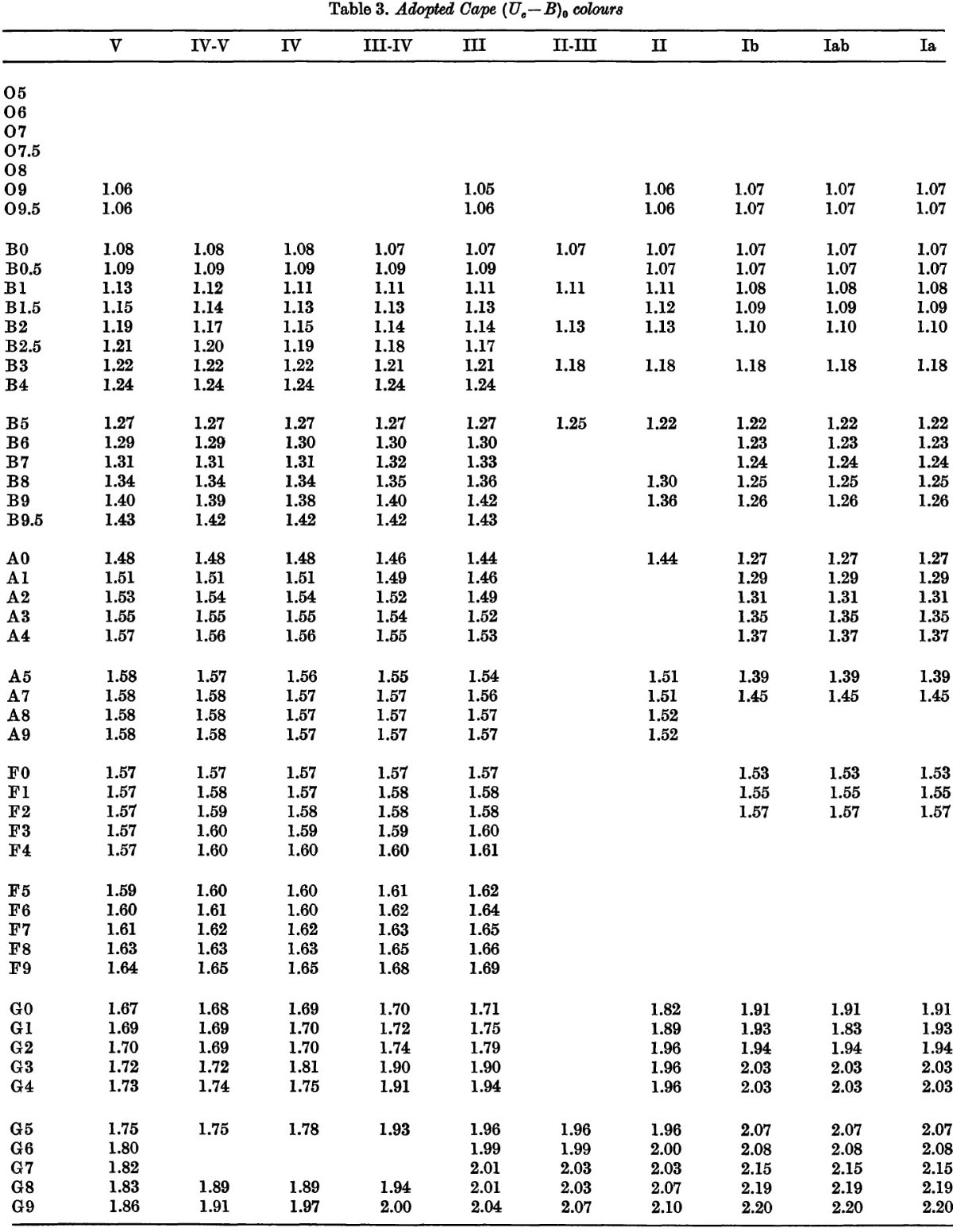
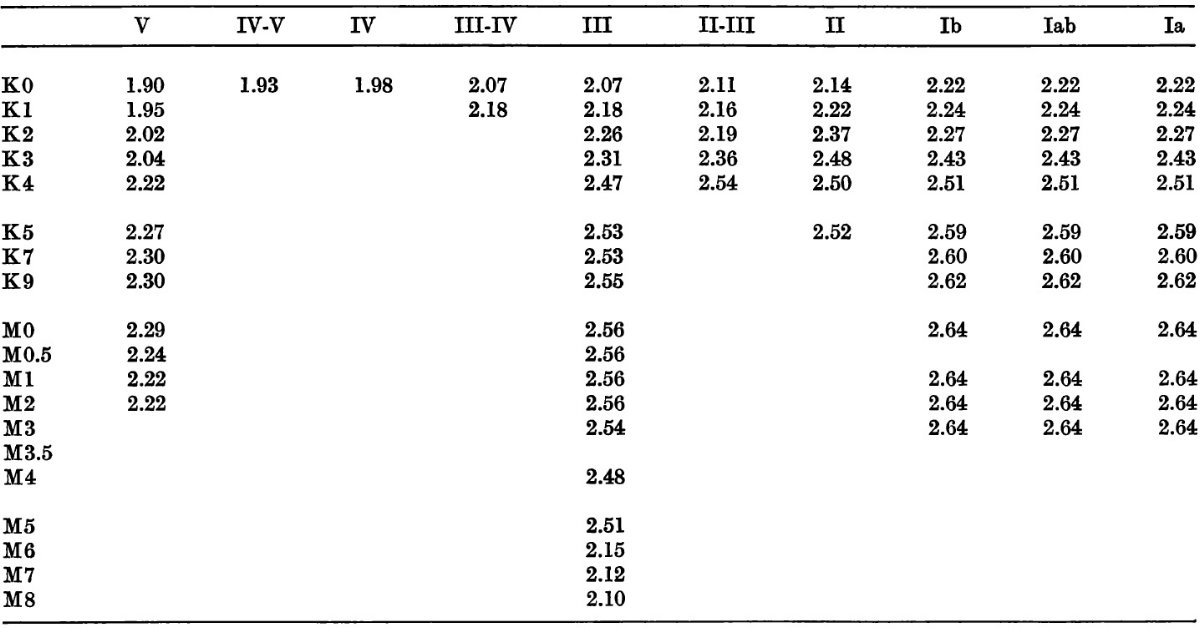
光電測光カタログ　 　Blanco 1968 の Photoelectric Catalogue には 17,000 星の Johnson UBV, Cape UcBV 等級が載っている。そのうち 7000 星は MK 分類が与えられている。 　固有カラー　 　理想的には無赤化星のカラーが得られればよい。これは A0 より晩期の 矮星と巨星では可能である。しかし、他の種類の星では同種類の星の２色図 を作り、その青端を固有カラーと仮定して求める。この方法は Feinstein 1959, Kraft, Hiltner 1961 が用いた方法である。Johnson 1963 は O-, B- 型星の 固有カラーを求めるため、より晩期の星で赤化が決まっている星団メンバーを 用いた。この方法は O-, B-型星にはうまく行ったが、A - M 型超巨星の場合は 星団中にサンプルが存在しないために働かなかった。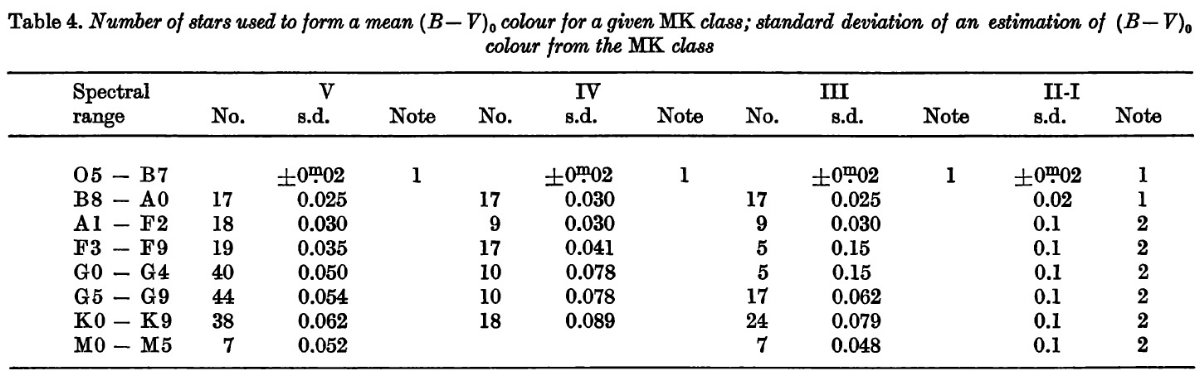 　無赤化星のカラー　 　スペクトル型 A0 より晩期、光度クラス III, IV, V の星は 100 pc 以内に 多数見つかる。 FitzGerald 1968, Eggen 1963 はこれ等の星の赤化が小さいことを示した。図１の　V - (B-V) 図は 100 pc 以内で赤化が無視できることを示している。このような方法で 　A0 III-V - M6 III-V の星の固有カラーが決められた。一般的には 固有カラーは 50 - 100 pc 以内の 10 - 40 星の平均として決まる。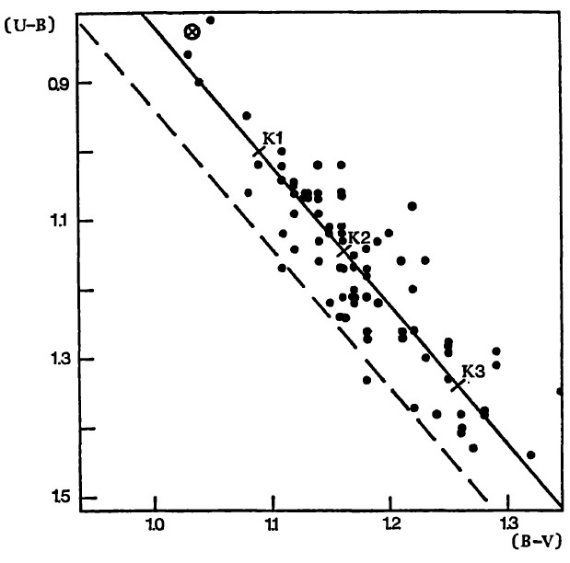 固有カラー二色図　 　得たカラーから (U-B)o - (B-V)o, (Uc-B) - (B-V) 二色図が作られる。

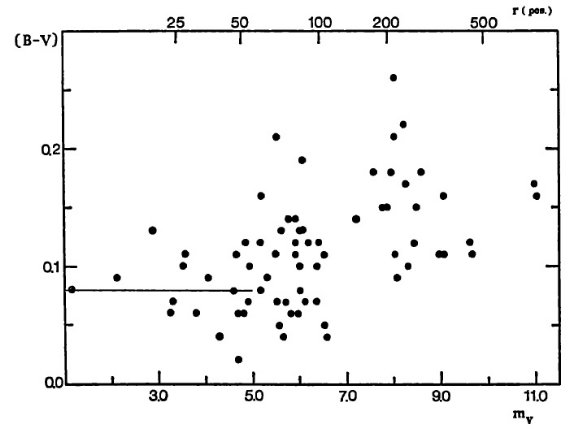
図１．A3V 星の (B-V) 対 mv 図。このグループの星の 固有カラーは 0.080 となる。

明るい巨星と超巨星　 　明るい巨星と超巨星は二色図の青端で固有カラーを決める。この方法の エラーは、 （１）無赤化の星がないと、青端でも赤化を受けている。 （２）無赤化星が多すぎると測定エラーで、端のカラーは青すぎる。 その効果を示すため、図２に既に固有カラーが決まっている K2 III の 二色図を示す。実線は既に決まった巨星の系列である。これで見ると青端法は K2III に対して、 0.04 mag 青い値を与えることが判る。 　二色図法は G5 より晩期の明るい巨星、超巨星に対して用いられる。それ より早期だと赤化ベクトルが固有ラインと複数回まじわるので、スペクトル 型ーカラー図を用いるべきである。 　光度グループ　 　三つの光度グループ、 (i) II - III, (ii) II, (iii) Ia, Iab, Ib が用いられる。A - G5 型星はスペクトル型ーカラー図から固有カラーを 決めた。 　O-,B-型星の赤化線と固有カラー　 　O-, B-型星のカラーは通常減光が既知の星団(Johnson 1963) から決める。 そうすると、フィールド O, B 星は使われない。それらの星を二色図に 並べ、固有 (B-V)o カラーと交わる点から (U-B)o を決めることが出来る。

図２．K2 III 星の二色図。実線＝近傍星から決めた III 巨星の経路。 その上に K1, K2, K3 をプロットした。破線＝分布青端のライン。 丸バツ印＝最青端にあたる星の位置。 (何のことなのか？丸バツはどうして 実線K2とこんなに離れるのか？ )

　 α　の変化？　

赤化勾配　 　　Eu = δu + αEy + βEy2 ここに、Eu = E(U-B), Ey = E(B-V) である。 　β = 0.05 を過去の研究やモデル計算から採用して、 α の 決定を行った。 　天空の分割　 　まず銀経を、l = 0° - 72°, 72° - 90°, 90° - 170°, 170° - 270°, 270° - 320°, 320° - 360° の６領域に分け、スペクトル型は O5-O7, O8, O9-O9.5, B0-B0.5, B1-B1.5, B2, B3-B4, B5-B6, B7-B8, B9-B0.5, B1-B1.5, B2, B3-B4, B5-B6, B7-B8, B9-B9.5, A0-A1, A2-A6 に分けた。O9-A5 はさらに光度クラス で Ia-II, III-IV, V の３クラスに分けた。こうしてできた 198 区間ごとに α を決めた。Wampler 1961 が述べたように、α の弱い l 依存 が認められるが、パラメターが大きく変わるのはシグナス領域である。 それで、空をシグナス領域とその他とに二分した。その結果、分割は 66 に なった。 α の変化　 　表２の (U-B)o と β = 0.05 の仮定に基づいて、上の各区間で α を決めた。O9 - B1 主系列星に対しては、 　　&alpha: = 0.752±0.011　　　Cygnus region 　　　　　　　0.699±0.006　　　他領域 であった。表５にはシグナス領域外での α をスペクトル型毎に与えた。 また、表６には (U-B)o に対する変化を示した。シグナス領域に対する 値は 0.053 を加えると得られる。 　Cape UcBV システム　 　Cape UcBV システムでの赤化軌跡も同じように求めた。こちらには、 銀経による変化は認められなかった。また、曲がり β = 0.00 で あった。MK 分類による変化もなかった。勾配の平均値は、 　　　α = 0.368 ±0.014 　　　O - B1 星 であった。

表５．MK 群ごとの赤化勾配 α 値 表６．M赤化勾配 α 値の (U-B)o による変化

　結果