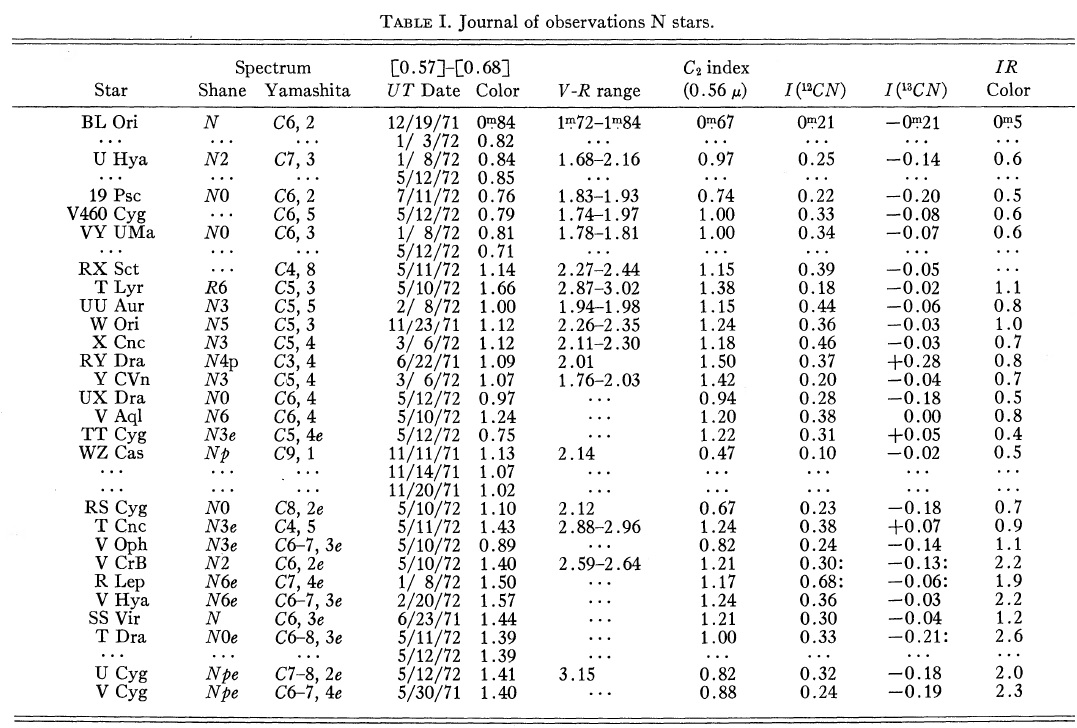
| 26 N-型、11 R-型星の 5000 - 7000 A, 分解能 20 A 光電スペクトル観測を 行った。カラー指数 [0.57]-[0.68] を定義し、(V-R)カラーと [3.5-11/0] 指数 との相関を調べた。新しい測光指数を CN, C2 バンド強度を測る ために改訂した。 | 我々の CN 指数は 12C/13C 比の推定に用いられる。 我々の 0.56 μm C2 指数は 1 μm CN 指数と正の相関を示し、 また 2.3 μm CO 指数と逆相関を持つ。モデル大気計算と比べると、 これらの関係は C/O の変化に起因すると解釈できる。 |

|
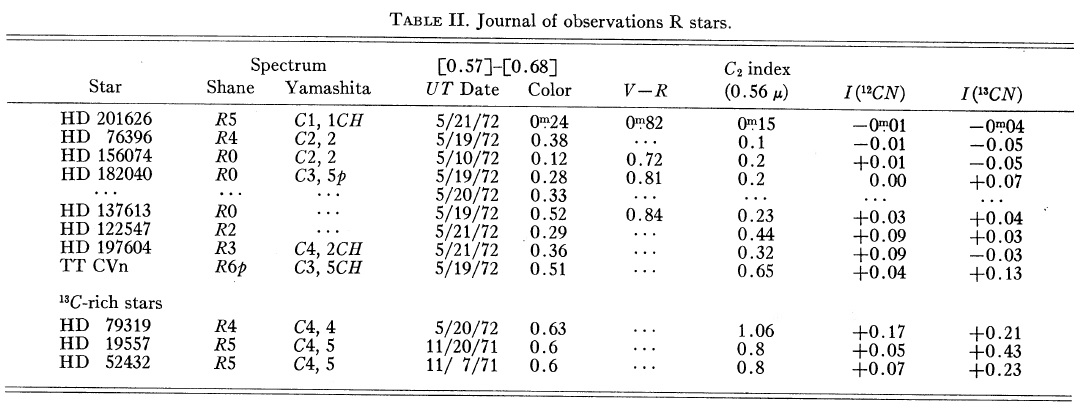
図1−5に観測スペクトル 観測は 1971 - 1972 年に Goethe Link 90 cm 望遠鏡にスキャナーを 取り付けて行われた。表1に観測ログを載せる。図1−5に観測スペクトル を示す。 6000 - 7000 A バンド 6000 - 7000 A では CN の Δv = 4 吸収帯、CN(4,0) λ6192, CN(5,1) λ6332, CN(6,2) λ6478, CN(7,3) λ6634 が 見える。 |
カラー指数 表1の第5列にはカラー指数が載っている。 [0.57]-[0.68] = -1.5 log[Fν(5710A)/Fν (6780A)] 特異星 T Lyr を除き、 25 個の N-型星では [0.57-0.68] = 1.3, 11 R-型 星では 0.41 である。この結果は、N-型星のカラー温度 2300 - 3000 K, R-型星のカラー温度 4700 - 5200 K と合う。 |
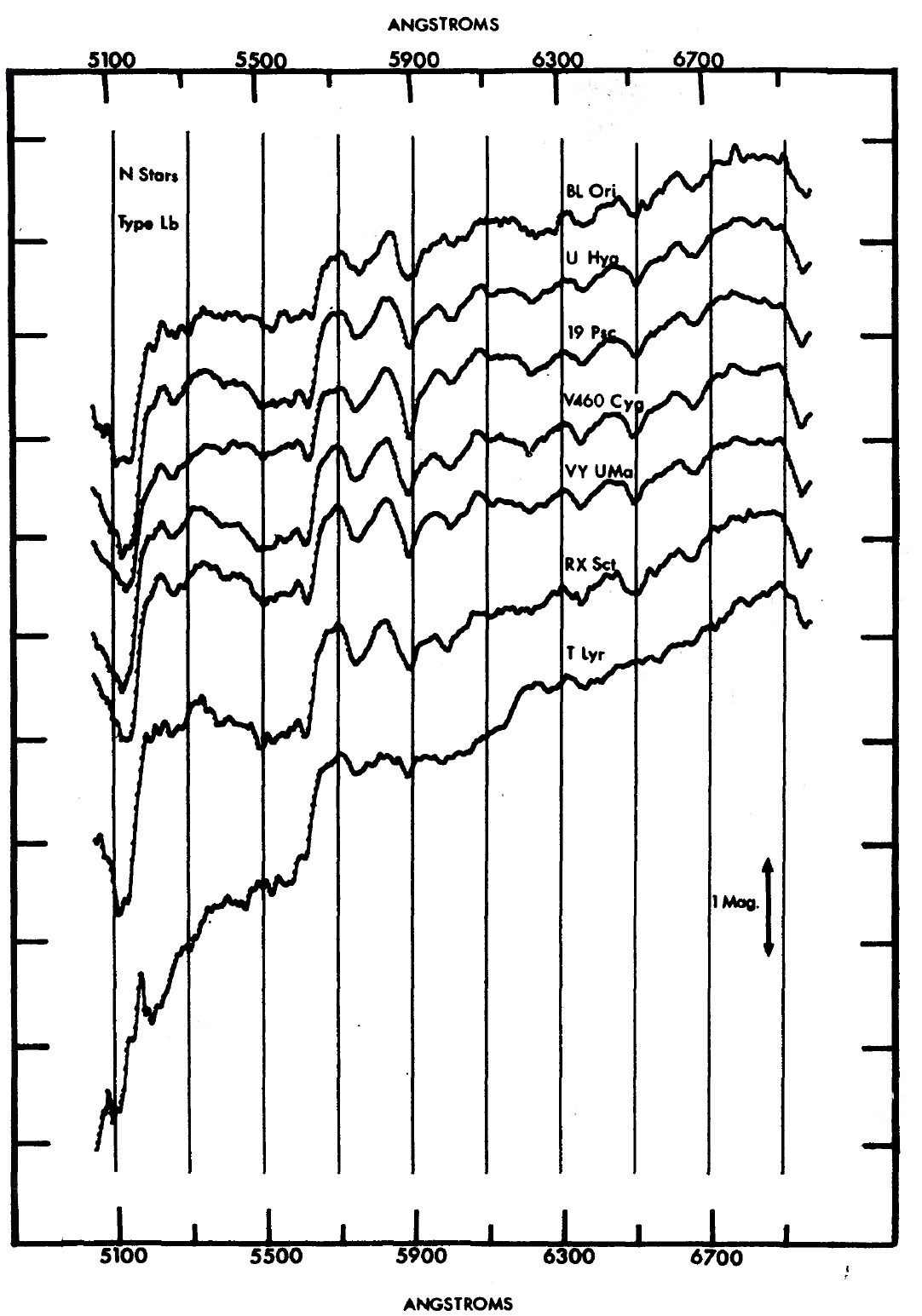
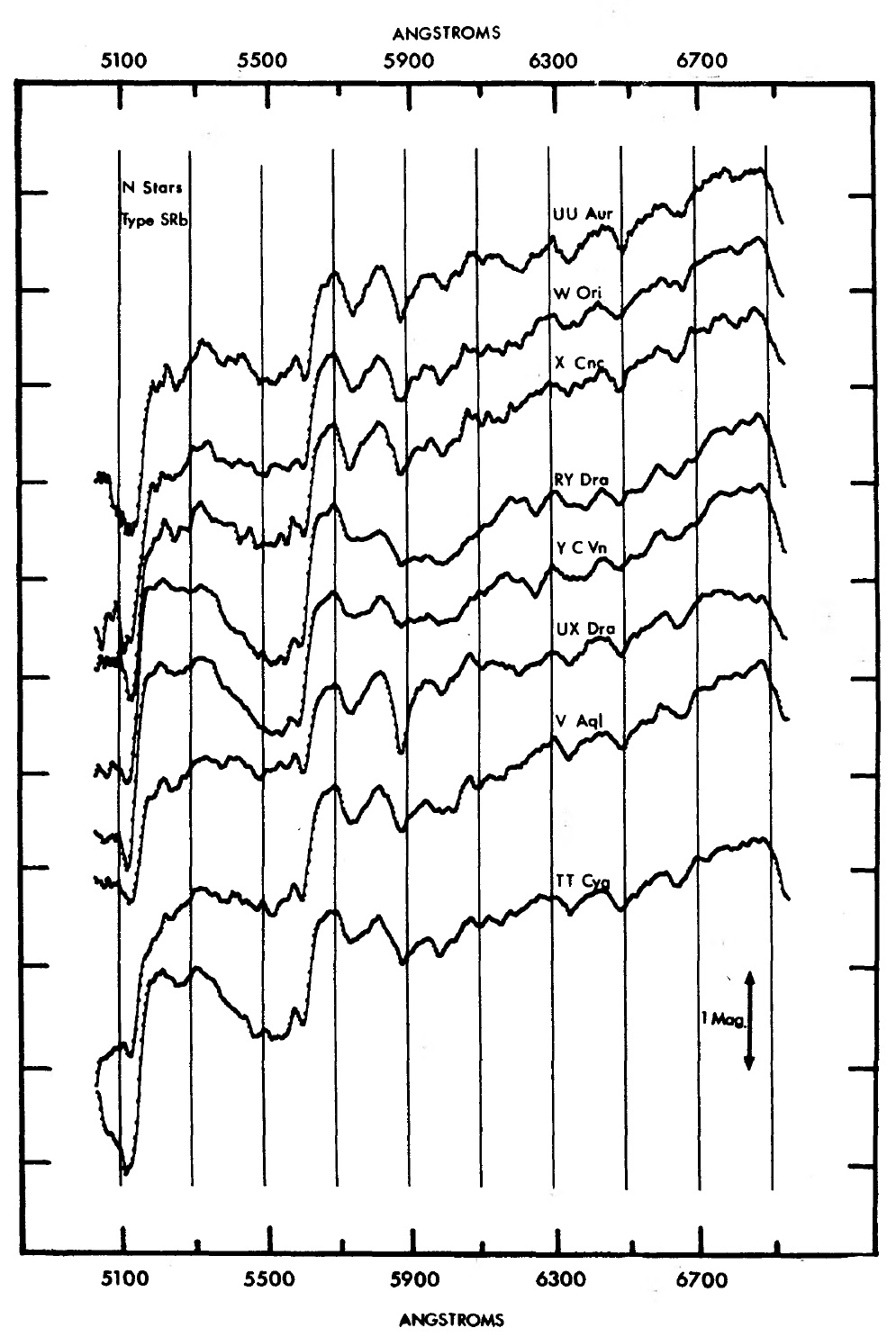
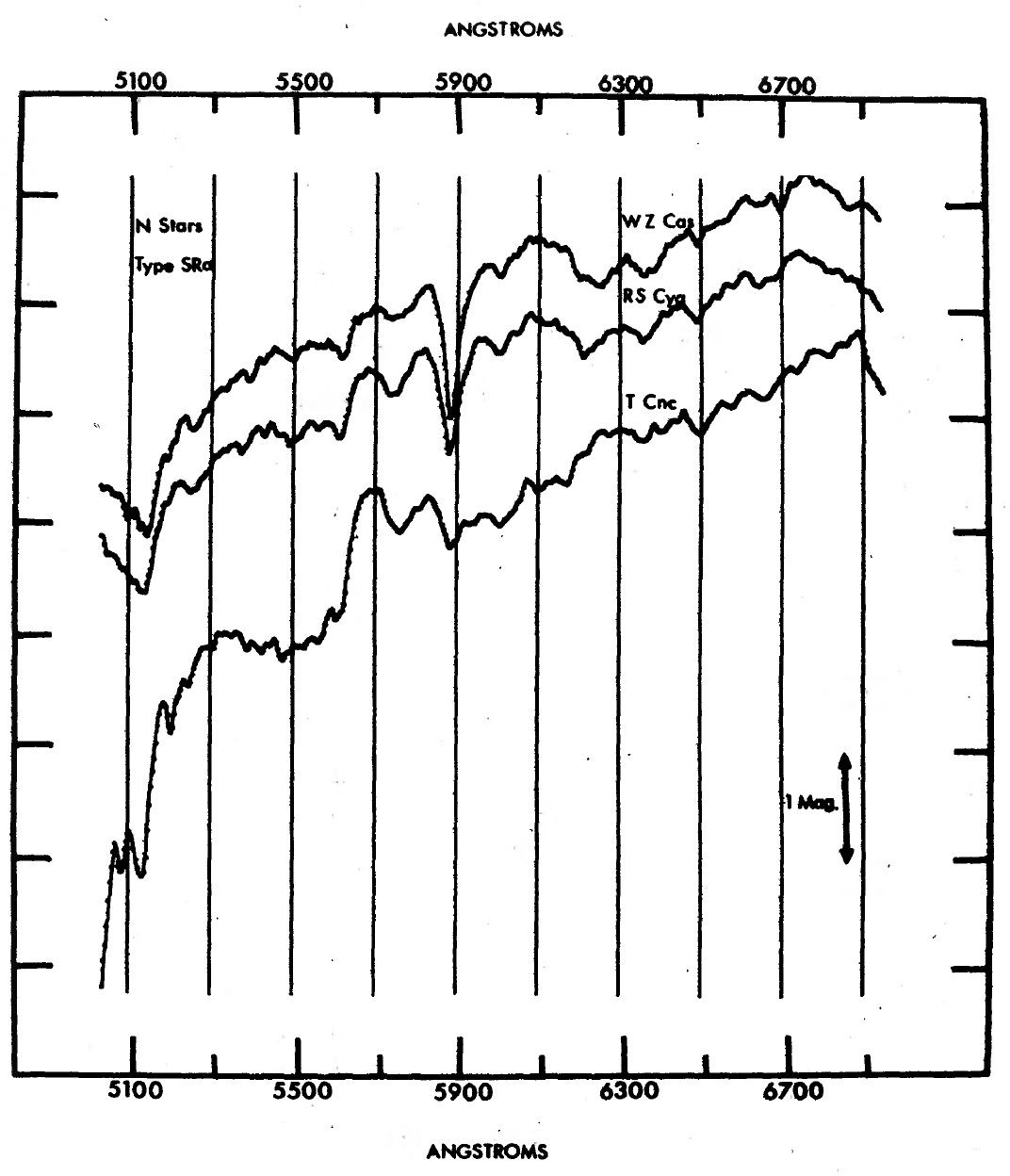
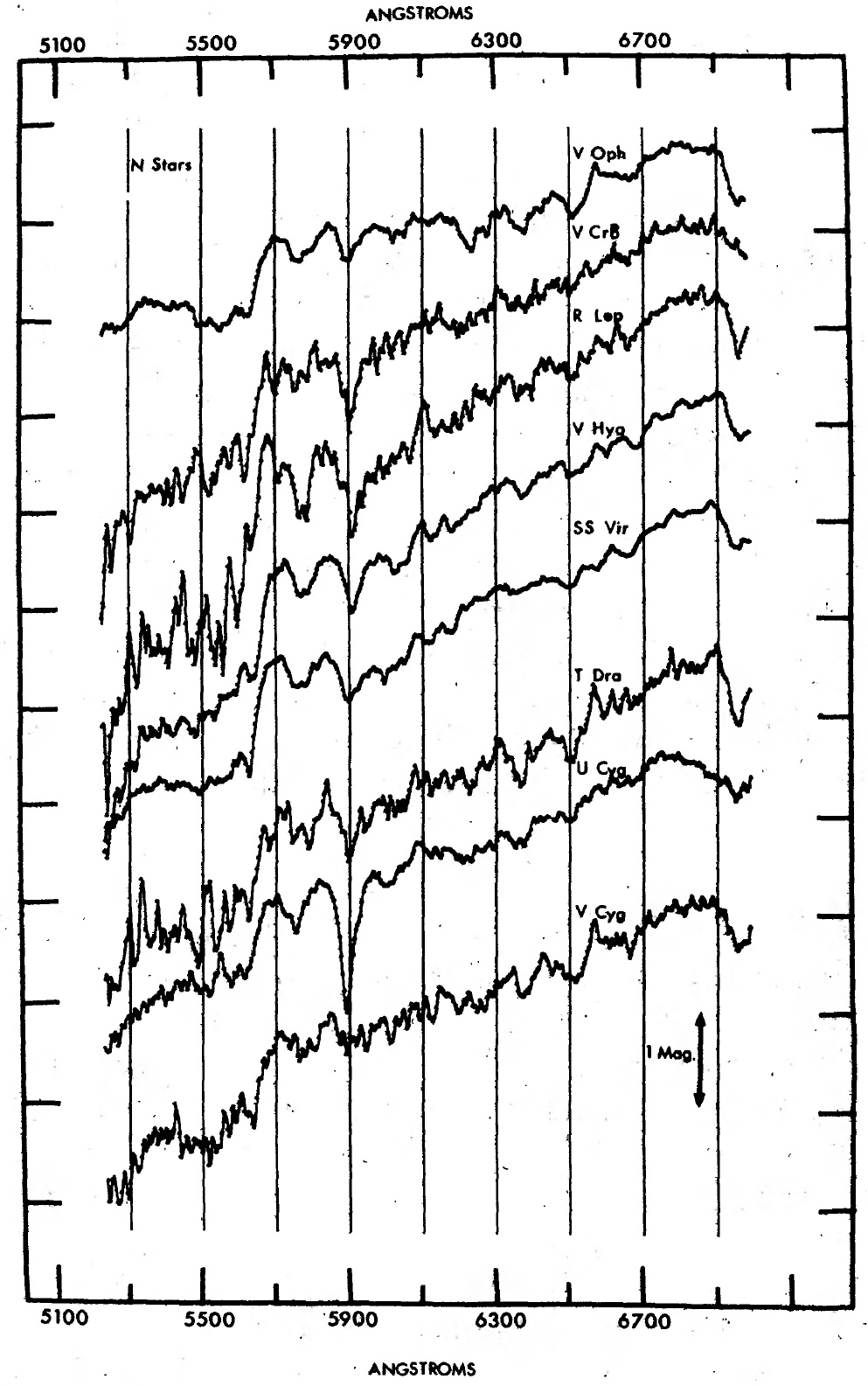
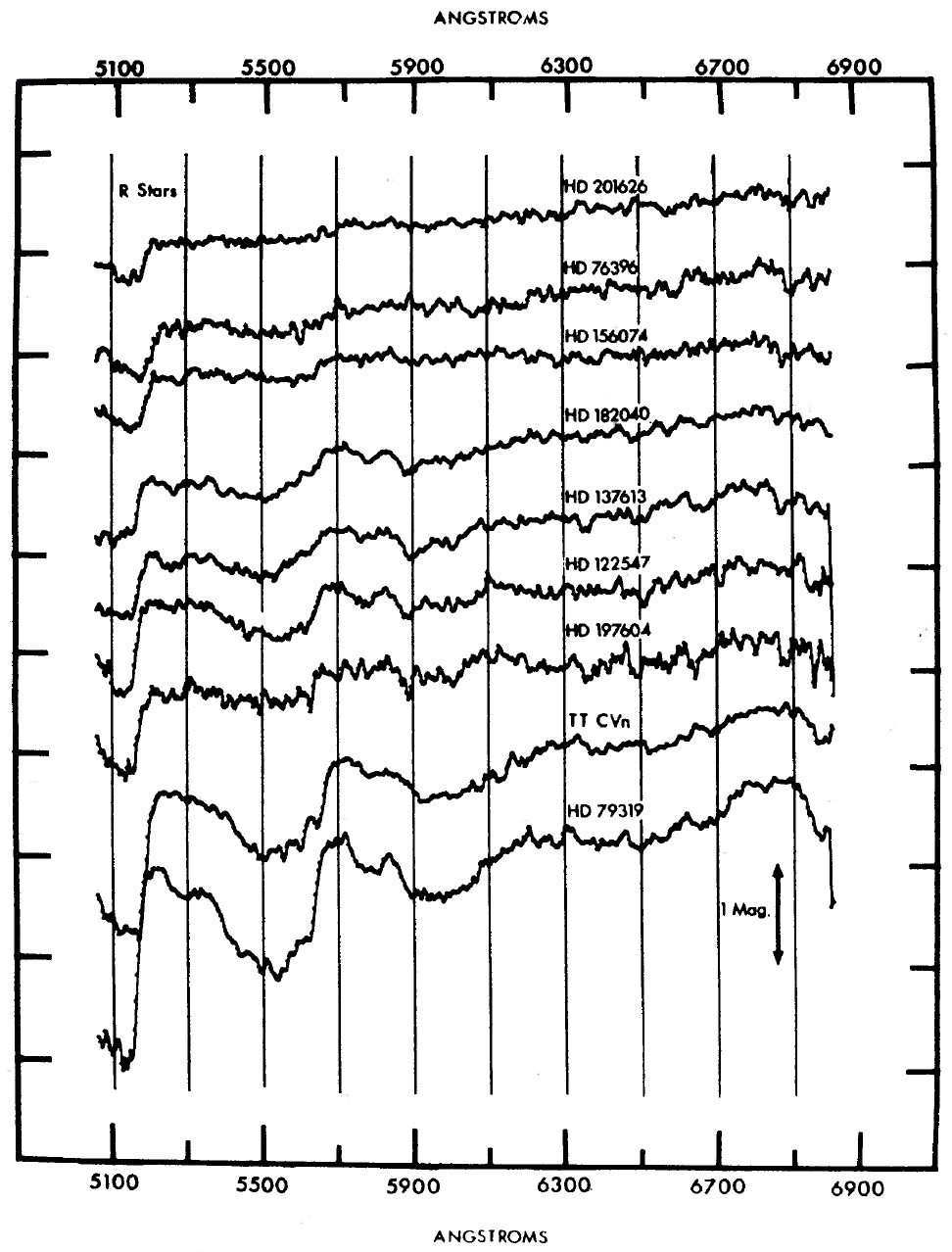
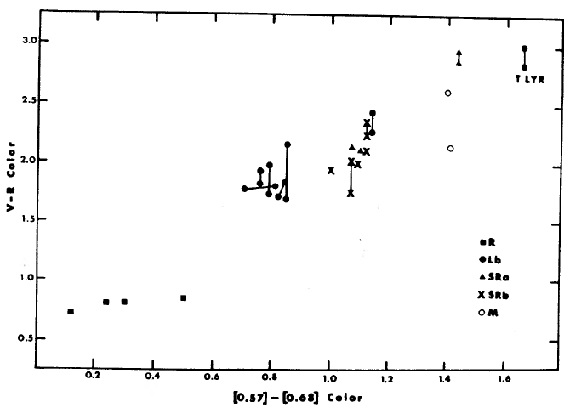 図6.21炭素星の (V-R) - [0.57]-[0.68] 関係。 (V-R) - [0.57]-[0.68] 関係 図6には (V-R) - [0.57]-[0.68] 関係を示す。相関は良く、(V-R) がカラー 温度の決定に利用可能であることを示す。 |
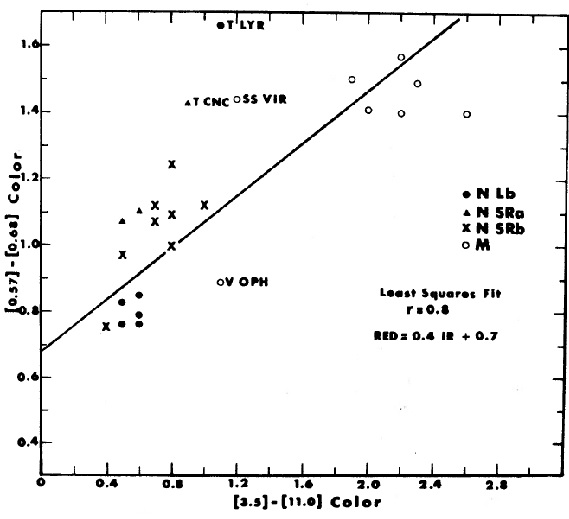 図7.25 炭素星の [3.5]-[11.3] と [0.57]-[0.68] の関係。 [3.5]-[11.3] と [0.57]-[0.68] の関係 図7には [3.5]-[11.3] と [0.57]-[0.68] の関係を示す。全体の関係は 実線で示されるが、変光タイプ毎では別の関係が可能に見える。 |
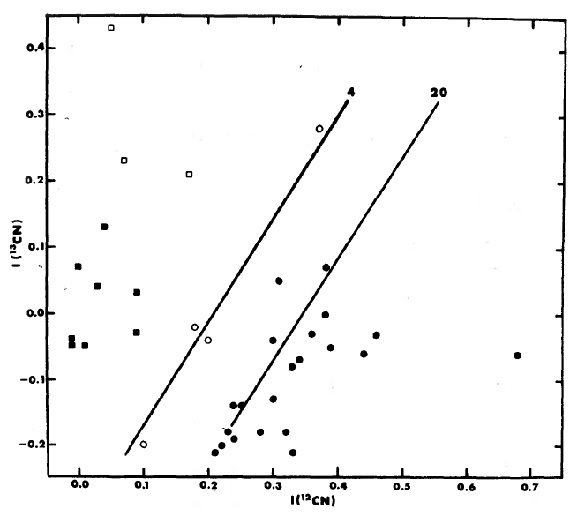 図8.我々の I(13CN)指数-I(12CN)指数関係。 黒四角=R-星。黒丸=N-星。白丸= J-星。直線=12C/13C 一定線。 CN 指数 12CN 指数と 13CN 指数 I(12CN) = -2.5 log[Fν(5730A)/Fν(5710A)] I(13CN) = -2.5 log[Fν(5810A)/Fν(5710A)] で定義する。 (5810 じゃなく 5900 に見えるが?) |
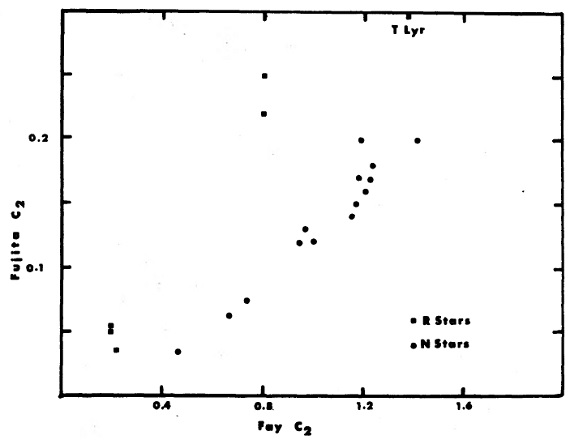 図9.藤田 1969 の 0.56 μm C2 指数とこの論文で定義した 0.56 μm C2 指数との関係。四角=R-星。丸=N-星。 図8=二つの指数の関係 図8から、互いの相関及び J-型星の分離は明らかである。この結果を見ると、 R, N, J 星の分離を測光だけで行える可能性がある。 新しい C2 指数 また、新しい C2 指数として C2(0,1) バンドヘッド強度を 以下のように定義する。 C2 指数 = -2.5 log[Fν(5610A)/Fν (5710A)] 図9にはこれを藤田の指数と比較した。これを見ると、我々の C2 指数 の有用性がわかる。 |
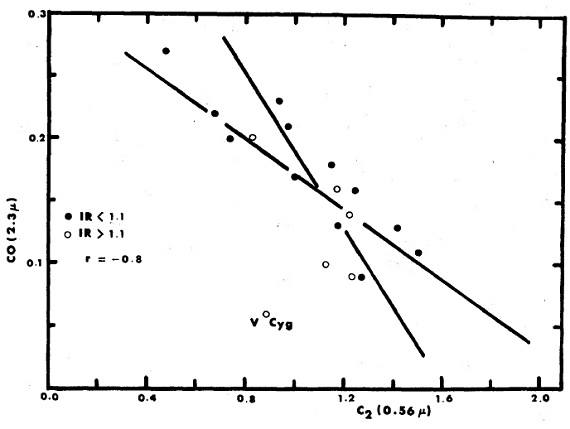 図10.2.3μm CO バンド強度と 0.56 μm C2 バンド強度の 関係。回帰線は赤外カラーの大きな V Cygni を除いて得られた。 較正は? 図8で R-,N- 分離が可能と分かったが、12C/13C の測定をどうしたらよいだろう?Johnson 1974 の炭素星モデル大気計算から Li I 共鳴線 λ6707 付近の合成 CN スペクトルを計算し、 19 PSc, WZ Cas, Y CVn の高分解スペクトルと比較した。その結果を用いて図8に 12C/13C 線を引いた。データ数が少ないのでこれを 定式化するのは尚早である。しかしサンプル数が増せばそれも可能となるだ ろう。 R-, N- 星の C2 指数 図9では R-星と N-星は異なる関係を持っている。藤田の 5900 A 連続光 はブランケッティングの影響を受ける。我々の指数の方はその影響が小さい。 CO 指数と我々の C2 指数 Frogel, Hyland 1972 は CO Δv=2 2.3 μm バンド強度を求めた。 彼らはその図4b で、 CO 指数と炭素星分類指数=基本的には C2 指数、との間の逆相関を指摘していた。ただその相関は信頼度 80 % では統計的に支持されなかった。しかし、我々の C2 指数 と彼らの CO 指数との間の逆相関は信頼レベル 90 % である。 |
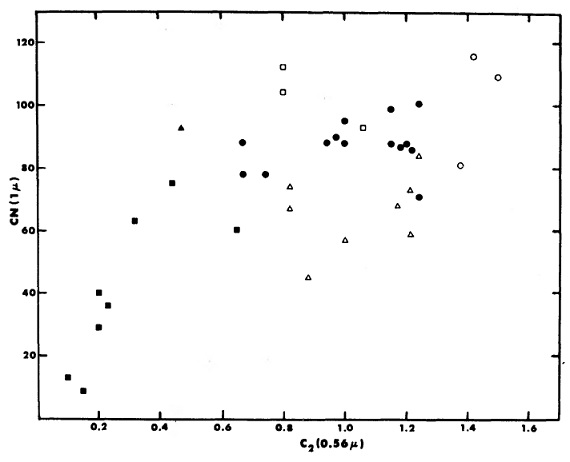 図11.1 μm CN 指数(Baumert 1972) と我々の 0.56 μm C2 指数との関係。黒四角= R-星。黒三角=WZ Cas. 黒丸= [3.5]-[11.0]<1.1 の N-星。白三角= [3.5]-[11.0]≥1.1 の N-星。 白丸と白四角= J-星。 1 μm CN 指数と C2 指数 図11には、1 μm CN 指数(Baumert 1972) と我々の 0.56 μm C2 指数との関係を示す。R-星と N-星が分離した系列にあることが 明瞭に見て取れる。ただし、赤外超過の大きな星は除く。これらの分離は温度 の差に依ると考えられる。R-星では高温のために CN と C2 双方 が弱いのであろう。 逸脱 [3.5]-[11.0] > 1.1 の星は系統的に弱い 1-μm 指数を示す。それらの 大部分はミラ型星で、1 μm CN が超過赤外光で埋められたのかも知れない。 Wing 1967, SSpinrad, Wing 1969 は彼らの CN 指数と炭素星分類指数との間に 相関を見出せなかった。その理由は、おそらく (1)3500 K より暖かい星を除いていた。 (2)11 μm 超過の大きな星を低超過の「裸」星から分離していない。 (3)Keenan 1971 炭素星指数は眼視評価で不正確である。 ためであろう。 |
|
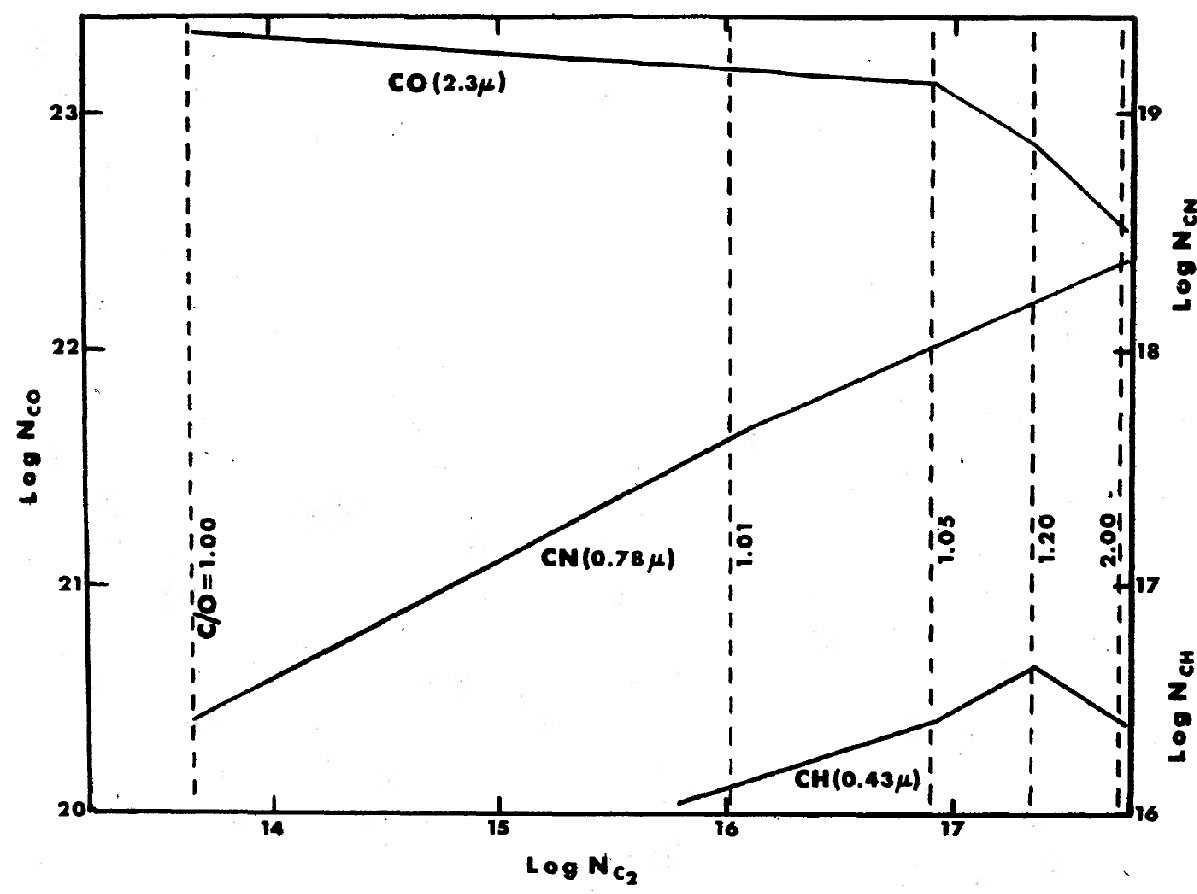
図12=コラム密度の関係 バンド強度間の相関を完全に理解するには詳細な大気モデルとの対照が必要 であるが、取り敢えずの形で C/O 依存性を調べた。 図12には、ATLAS 低温度星コード Kurucz 1970 を用いて計算した CO, CN, C2 のコラム密度の関係を Teff = 3000 K, log g = 0.0, [N/H]=0.0, [O/H]=0.0, C/O = [1, 5] に対してプロットした。 コラム密度は cm2 あたり、τλ = 0.3 までの分子数である。 (τλって?) オパシティは H, H-, H2, H2-, H2O, CN, CO Alexander, Jphnson 1972, 原子ラインブランケッティング Mutschlecner, Keller 1972, それに C2 Main, Bauer 1967 である。 グラフの特徴 明らかに観測された傾向はうまく再現されている。最も興味深いのは N(CO) と N(C2) の逆相関である。この効果は C/H が増すにつれて 主に CN により大気オパシティが上昇するために、ガス密度を減少させ、光路 長を短くする。このため多くの分子コラム密度は低下する。例外となるのは、 C/H 増加と共に数密度が著しく増加する分子で、その効果が光路長の縮小を上 回るのである。 |
CO, CN, C2 コラム密度 CO の数密度は増加するのであるが、光路長の短縮効果のため CO コラム密度 は低下する。CN の数密度とコラム密度はどちらも上昇する。C2 は激しく増加する。 低炭素の炭素星 予備的計算によれば、図10の炭素星と同じように、[C/H] < 0 の低炭素 量星や [N/H] > 0 の高窒素星でも CO, CN, C2 コラム密度 の傾向は同じである。 低炭素の炭素星では C2 コラム密度が低すぎ、Teff > 3000 K では C2(0,0) スワンバンドを生み出すに足りない。 |
|
[0.57]-[0.68] カラー 炭素星に向いた新しいカラー指数 [0.57]-[0.68] を定義した。予想通り、 (V-R) との相関はよく、(V-R)が温度指数として有用であることを確認できた。 CO 指数 CO 指数は C2 指数と逆相関にある。 |
CN 指数 12CN 指数を新しく定義した。これは既知の Wing(1967), Baumert (1971) 指数と相関がよい。また 13CN 指数と組み合わせると、 12C/13C の測光観測が可能になる。1 μm CN 指数は 我々の C2 指数とよい相関にある。 |