Radial Pulsations of Stars on the Stage of the Final Helium Flash


Fadeyev
2019 arXiv:1909.04500v1,



　アブストラクト　

　冷却過程の種族 I 白色矮星, Mi = [1, 1.5] Mo, の進化計算を行った。 オーバーシューティングパラメター f = 0.016 モデルでは、Mi = [1.3, 1.32] Mo の post-AGB 星で最終ヘリウムフラッシュ LTP が起きる。もっと高効率 f = 0.018 では [1.28, 1.3] Mo で LTP が起きる。マスロスパラメター η を５倍変えたが、 LTP には影響せず、進化時間を変化させたのみで あった。Mi = 1.3 Mo に対し、 f = 0.016 と 0.018 の二つの値で、LTP 期 の動径振動のモデル計算を行った。 　Mi=1.4 Mo, f=0.016 モデルでの最長周期 P = 117 日は FG Sge の観測値 に合う。その時、 M = 0.565 Mo, R = 126 Ro, Teff = 4445 K である。 しかし　GD Sge の周期変化率 1960 - 1990 はモデル値の３倍である。

　１．イントロダクション　

　最後のヘリウムフラッシュ　

　Bertolami 2016 の計算では、post-AGB 期 (Menv/M = 0.01 から Teff = 20,000 K まで）は 34,000 年（Mi=1Mo) から 600 年 (4Mo) である。 post-AGB 星のエネルギー源は水素燃焼であるが、それが停止する前に ヘリウムフラッシュの起きる可能性がある。（Schonberner 1979） Blocker 2001 は最終ヘリウムフラッシュが起きるのは、LTP = 水素燃焼 期間中か、VLTP = 水素燃焼終了後白色矮星期か、とした。進化経路は Teff = 4000 K という低温領域まで下がる。

　LTP 星？　

　幾つかの PNe 中心星の等級、スペクトル変化、FG Sge, V4334 Sgr, V605 Aql が LTP モデルで説明される。モデル計算による変化速度は観測と良く合う。 		　FG Sge　

　PN He1-5(Henize 1961) の中心星 FG Sge はもっとも良く調べられてきた 最終へリウムフラッシュ星である。観測は 130 年に及び、この間に 1880 年の Teff = 45,000 K から 1992 年の 4500 K まで下がった。さらに、６０年間 に FG Sge の周期は 1930 年の 5 日から 1986 - 1989 年の 115 日にまで上昇 した。周期増加は 1990 年以降停止している。（arkipova et al 2009）

　振動計算　

　ここでは、振動計算を観測と比較する

　２．進化計算　

　オーバーシューティング　

　進化計算は MESA version10398 で行った。対流は α = l/Hp = 1.8 の ミクシング長モデルで扱う。オーバーシューティングは Herwig 2000 に従う。

　　　Oov(z) = Do exp(-2z/fHp)

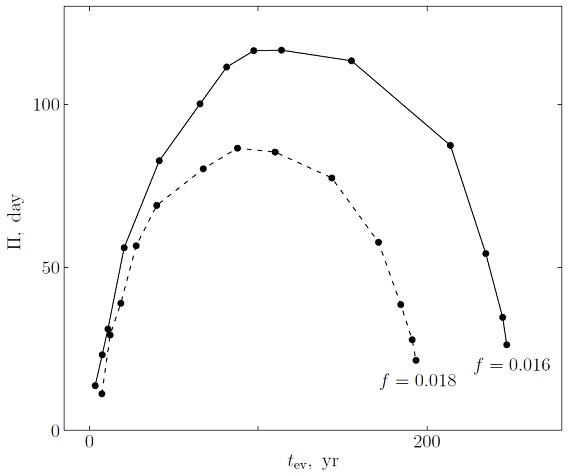
ここに、 Do ＝ 対流拡散係数(Langer et al 1985) で、Schwarzschild 境界 から 0.004Hp 離れた点での値である。f = オーバーシューティングパラメター。 f の影響を見るため、 f = 0.016 (通常使われる値) と f = 0.018 の二つで 計算した。

　マスロス　

　AGB 期より前の計算は Reimers 1975 のマスロス則、

　　(dM/dt)R = 4 10-13ηR (LR/M) Mo/yr

で計算した。 一方、 AGB 期は Blocker 1995 のマスロス式

　　(dM/dt)B = 4.89 10-9ηB L2.7M^2.1 (dM/dt)R Mo/yr

を採用する。ηR＝ηB=0.5 とした。 post-AGB で信頼できるマスロス式は存在しない。ここでは仮に前出の Blocker の式を使用する。マスロスパラメターηp = [0.02, 0.1] で計算してその効果を確認する。

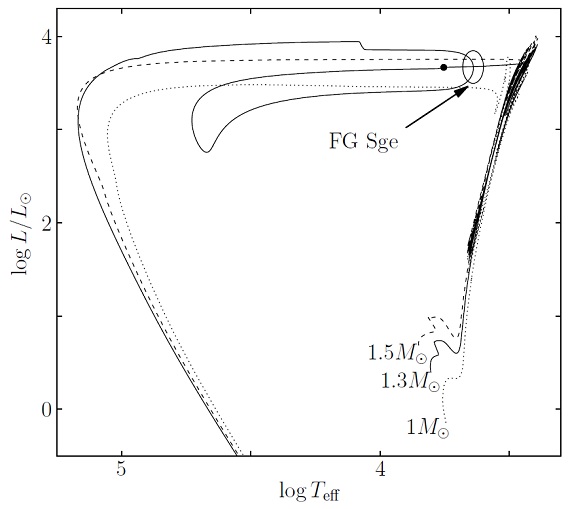
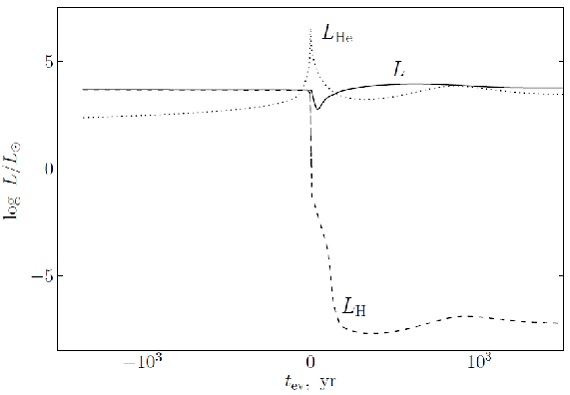
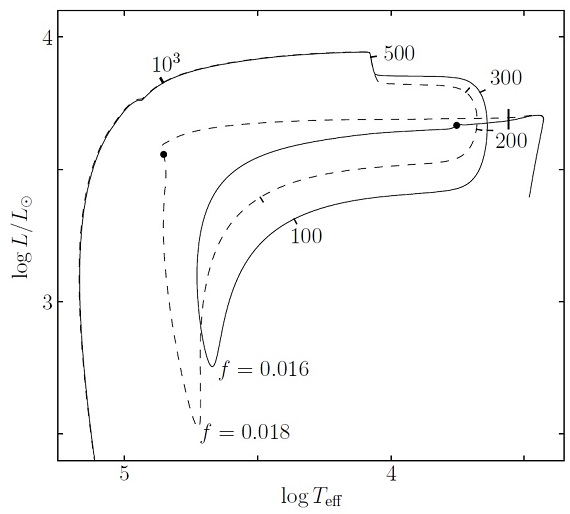
図１． 点線＝１Mo. 実線＝1.3 Mo. 破線＝ 1.5 Mo. f = 0.016, η p = 0.05 仮定。 黒丸＝ヘリウム燃焼の極大。楕円＝FG Sge の大体の位置。


図２．最終ヘリウムフラッシュ期における LH, LHe, L = LH + LHe の時間変化。Mi = 1.3 Mo, f = 0.016, ηp = 0.05. L

　図１は Mi = 1, 1.3, 1.5 Mo の進化経路　

　図１は Mi = 1, 1.3, 1.5 Mo の進化経路を表す。M = 1.3 Mo 進化のループ は最終ヘリウムフラッシュによる。図２には Mi = 1.3 Mo, f = 0.016, ηp = 0.05 での LH, LHe, L = LH + LHe の時間変化を示す。便利のため、時間 t はヘリウム燃焼極大をゼロとした。 水素燃焼は回復せず、ヘリウム燃焼が次第に衰え、白色矮星となる。

図３．Mi = 1.3 Mo, ηp = 0.05 の進化。実線は f = 0.016. 破線は f = 0.018. 黒丸＝ヘリウム燃焼の極大。数字＝縦線（post-AGB 開始） からの年数。

　LTP 出現範囲　

　図３にはオーバーシューティングパラメター f = 0.016 と 0.018 との違いを 示す。f が上がると ヘリウムフラッシュ時期が遅れる。しかし、そのどちらも LTP である。 その後の変化はほぼ同じ経路に収れんする。結局、 f = 0.016 では、 Mi = [1.30, 1.32] Mo で、f = 0.018 では Mi = [1.28, 1.30] で LTP が 出現する。

　図４＝パラメターによるモデル変化　

　図４には f, ηp を変えたときのループ上温度が下がり 半径が増加していく際の進化経路の違いを示す。 便利のため、Teff = 10,000 K の時を tev = 0 とした。

　LTP 期 R 最大時の星パラメター　

　表１には LTP 期に R 最大となる時の星パラメターを示す。


表１．LTP 期に R 最大となる時の星パラメター

図４．(a) ηp = 0.05 で f = 0.016(実線). f = 0.018(破線) の場合の経路。 (b) Mi = 1.3 Mo, f = 0.016 の場合、ηp による差。 　



　３．結果　


図５．断熱指数 Γ1 と質量座標 (1-Mr/M) の関係。 Mi = 1.3 Mo, f = 0.016, ηp = 0.05. R = 125.4 Ro, Teff = 4445 K. 　

図６．P の時間変化。Mi = 1.3 Mo, f = 0.016(実線), 0.018(破線) 　

　P 変化の比較　

　図６と図７を比較すると、M = 1.3 Mo, ηp = 0.05, f = 0.016 のモデルが観測に合う。特にモデルの最大周期 117 日が 1990 年以降安定している FG Sge 周期に近いことは注目に値する。　

図７．FG Sge の周期変化。様々なデータを集めた。実線はそのフィット。 　

　４．結論　

　FG Sge のこれまでの変光周期変化をほぼ合わせられるモデルパラメター が得られた。今後予想される周期下降期の観測が重要である。