| 種族I、初期質量 1, 1.5, 2 Mo の星の進化を PPN まで計算した。振動の初期 状態として Teff = [3.6, 20] 103 K の post-AGB 星を選んだ。 輻射流体力学と時間依存対流の解を用いて、動径振動する post-AGB 星の流体 力学モデルの系列を得たのは今回が初めてである。この温度領域で、post-AGB 星は基本振動が支配的で、星の進化に伴い P は 300 日から数日まで変化する。 | 非線形効果により周期の揺れが起き、それは Teff < 5000 K で著しい。 光度変化の振幅は Teff = 6000 K で ΔMbol = 1 であり、温度上昇に伴 い低下する。この研究で得られた、周期と有効温度の関係 （P-T 関係）は post-AGB ではないかと疑われる脈動変光星の進化段階の診断に使用できる。 |
|
post-AGB 星変光 TAGB での強い星風は非線形脈動効果(Tuchman et al 1978)による力学的不 安定性によると言われ、厚い星周層を作る。post-AGB 星の脈動変光は 200 日 から数十日に渡る。 Arkhipova et al 2017 は AI CMi が P = 310 日の早期 post-AGB ではないか と述べている。post-AGB 星変光の特徴は規則性の欠如で、周期の決定は困難である。 非線形振動 脈動不安定性の線形解析の結果は、post-AGB 星の不安定帯が Teff = 10,000 K まで伸びていることを示す。しかし、post-AGB 星のように L/M = 10,000 近い場合、外層の低い密度と小さな断熱指数により、非断熱性が 大きくなり、非線形振動が卓越する。 |
対流の重要性 流体力学計算から、低質量で中間スペクトル型の超巨星では、動径振動は大 きな振幅を持ち、非線形性が原因で周期が固定しない。また、これまでの計算 では無視されてきたエネルギー輸送における対流の効果は、特に Teff < 5000 K, P > 50 日では大きい。 恒星進化計算 今回の仕事は T = [3.6, 20] 103 K の post-AGB 星における 非線形振動を調べることである。恒星進化の計算は MESA コードを使って、 主系列星から Teff = 20,000 K の PPN まで行った。詳細は Fadeyev 2018. 種族 I X = 0.70, Y = 0.28 を仮定している。 |
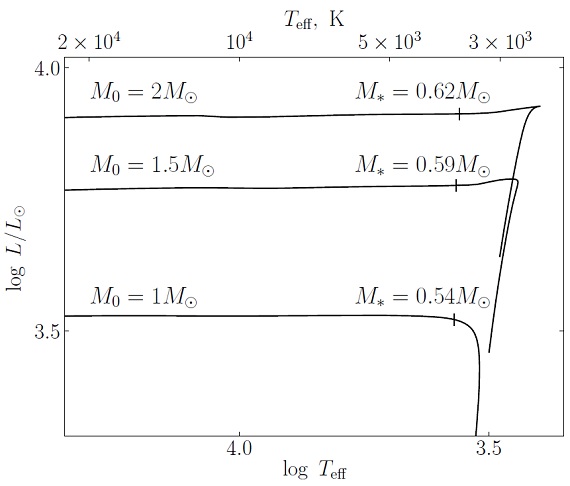
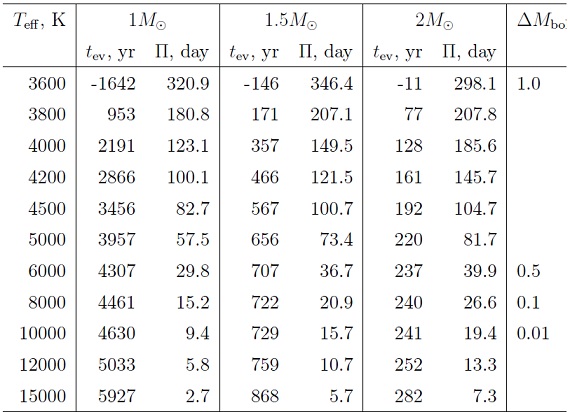
 図１．初期質量 M = 1, 1.5, 2 Mo 種族 I 星の AGB と post-AGB での進化 経路。M* = post-AGB 開始期の質量。 post-AGB 期の始まり 図１には Mi = 1, 1.5, 2 Mo の進化系列を示す。AGB 部は最後のヘリウム フラッシュから後のみを描いてある。この期間に水素外層の質量 Menv は大幅 に減少する。Bertolami 2016 に従い、 post-AGB 期の始まりを Menv/M = 0.01 の時と定義する。図１には縦マークでスタート点, tev = 0, を示した。 進化と質量の関係 Teff の時間変化を図２に示す。表１には post-AGB 開始期の星の性質 を載せた。Δtev は Teff = 20,000 K になる時の tev である。Mi が 1 Mo から 2 Mo になると、Δtev は 1/20 になることに注意せよ。 |
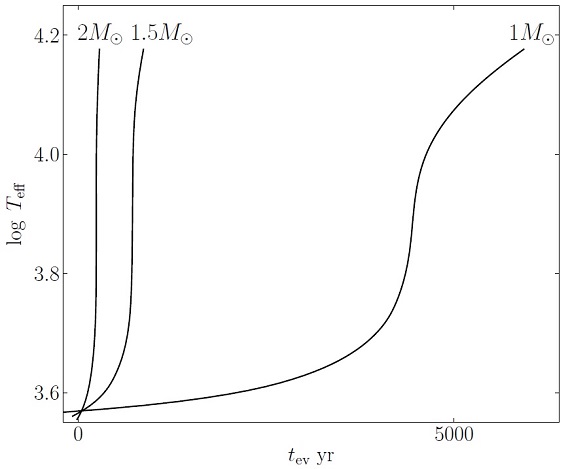
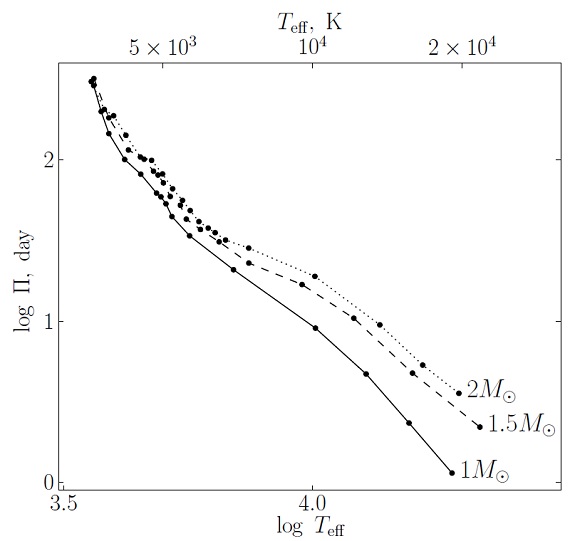
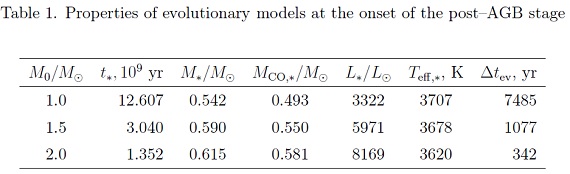
 図２．post-AGB 星の有効温度 Teff と時間 tev との関係。  表１．post-AGB 開始期の星の性質。 |
 図３．流体力学モデルの振動運動エネルギ Ek の規格化パワースペクトル。 初期質量 Mi = 1.5 Mo.実線は Teff = 4800 K, 点線は Teff = 6500 K. 図中の数字は、Po = 基本振動モードの平均周期。 電離層 post-AGB 進化と共に、星半径ばかりでなく、水素とヘリウムの電離層の質量 も減少していく。その結果、脈動周期の低下には脈動不安定性と非線形 性効果の低下も伴う。Teff < 4000 K では動径振動は外層のかなりを占める 水素電離層により駆動される。Teff がそれより高くなると、振動はヘリウム 電離層で駆動される。 非線形解と周期 AGB 星の非線形振動の論文(Fadeyev 2017, 2018)で述べたように、振動周期 は振動外層の運動エネルギーをフーリエ変換して定める。こうして、各流体力 学モデルの周期は一定期間に亘る解を平均して決まるのである。大部分のモデル では、解は１００周期程度である。 パワースペクトル post-AGP 進化の間での非線形効果を図３に示す。Teff = 4800 K の時、 運動エネルギーの成長率は η = P dlnEk/dt = 1.3, 平均基本振動周期 Po = 85 日、サイクル毎の周期は非線形効果により Po の 20 % に広がる。 一方、Teff = 6500 K の時、η = 0.04, Po = 31 日、サイクル毎の 周期の広がりは Po の 数 % である。 周期の低下 図４には、進化系列モデルに沿った、 Teff と P の関係を示す。 post-AGB の始まりには、どの初期質量でも P = 300 日である。 Teff が 20,000 に上がる間に、周期は二桁低下する。表２には進化時間 tev と周期 P の関係を示す。表２には振幅 ΔMbol も載せた。 Teff < 6000 K では ΔMbol = 1 程度だが、 8000 K になると ΔMbol = 0.1 まで下がる。 |
 図４．黒丸＝進化系列モデルに沿った、 Teff と P の関係。初期質量は、 実線＝ 1.0 Mo, 破線＝ 1.5 Mo, 点線＝ 2 Mo.  表２．tev = 進化時間と P = 周期の関係。 |
|
Mi = 1 Mo が大事 進化計算と非線形振動計算の結果を示した。Mi = 1 から 2 (または 1.5) Mo の間に進化時間＝ Teff 3600 K から 20,000 K まで、が 20 分の一になる ということから、観測されている post-AGB 星の殆どが Mi = 1 Mo であると 結論される。観測とモデルのより詳細な比較のためには、モデルをさらに拡大 させる必要がある。 |
例 = AI CMi GCVS によると、AI CMi は G5Iab のセミレギュラー P = 230 日である。 このスペクトル型だと Teff = [4500, 5000] K であるから、表２からは モデル周期は P ≤ 100 日となり、観測値の半分以下である。観測周期の 不定性は post-AGB 星の進化段階の研究で大きな障害である。したがって、 上に述べた矛盾を調べるには、より精密な変光観測が重要である。 |