| 太陽 1 kpc 内の早期型星空間分布を解析するために、新たに３次元空間分類 法を開発した。分布モデルとしてグールドベルト円盤＋局所銀河円盤を考える。 | B6 型より早期で光度クラス III - V で測光距離 1 kpc 以内の星 550 個を用 いて、あるスペクトルグループの星に対し、分布モデルのパラメターを決めた。 |
|
グールドベルトの発見 ハーシェル 1847, ストルーブ 1847, グールド 1979 は、明るい星は銀河とそ れに 20°の角度で交わる二つの線に沿って並ぶことに気付いた。Lesh 1968, Stothers, Frogel 1974 はグールドベルト(GB) は太陽近傍に平面状に分布す る O, B-型星の集まりであるいことを見出した。 |
最も近い星形成複合体 グールドベルトは滑らかな星の分布ではなく、その運動学は銀河面を構成 する OB-星と異なる。また、ダスト、HI, CO の特徴の幾つかはグールド ベルトに付随する。そこから、我々が見ているのは空間スケール 1 kpc の 星形成過程であるという考えが生まれた。グールドベルトは我々に最も近い 星形成複合体なのである。Poppel 1997, Grenier 2006 の概説を見よ。 |
|
第１の方法 第１の方法では空間位置 (X, Y, Z) から円盤との距離を求めある限界値内の 星をグールドベルトに属すると決める。利点は簡単であることだが、銀河円盤星 の混入、特に交差帯で、の処理が問題となる。 第２の方法 第２の方法は二つの系の天空上の分布を死す関数で近似して、最尤法を適用 することである。 第３の方法 Stotherts, Frogel 1974 は二つの面までの距離を比較した。（第１と 同じに見える。第１と言っているのは XY, XZ, YZ の投影で議論してるらしい） |
 図１．交差する二つの面。 |
|
新しい３次元空間分類法 新しい３次元空間分類法を考えた。GB と LGD の二つの面を考え、個々の星が そこに属する確率を計算する。そして、単純に面までの距離を較べるのでなく、 星の分布確率密度を考える点が新しい。 |
サンプル OB 星サンプルはヒッパルコスカタログから採った。 |
２．１．空間モデルグールドベルトの平均面を、a1*X + a2*Y + a3*Z + a4 = 0 とする。a1*a1+a2*a2+a3*a3 = 1 である。 ２．２．統計処理ベイズ推定ベイズ法については Cabrera-Cano, Alfaro 1990 を見よ。 平面のパラメターが既知であるなら、各系の確率分布関数 φGB, φLGD が計算できる。ある星が GB に属する事前確率 fGB が分かっているなら、事後確率 pGB は、ベイズ定理により次のように書くことができる。 pGB = fGBφGB/ {fGBφGB+(1-fGB)φLGD} pGB > 0.5 ならばこの星をグールドベルトに所属すると言える。 |
逐次法 我々にはそこから面パラメターが決まる事前に分類されたサンプルは与え られていないから、逐次法が必要である。面パラメター、fGB、 スケール高 hGB, hLGD の初期推定値から出発して、 第２の推定値に進むという過程を繰り返す。 ２．２．１．主アルゴリズム２．２．２．アウトライヤー |
 図２．模擬サンプルの分類例  図４．模擬サンプルに対する評価テストの結果。 |
 図３．図１と同じ円盤パラメター（破線）を用いた模擬グールドベルトに対する 評価テスト。各点は１００テストの平均を示す。 |
 図５．ヒッパルコス距離とストレームグレン測光距離の比較 ヒッパルコスカタログ ヒッパルコスカタログからスペクトル型 O - B6 で光度クラス III, IV, V の星を選んだ。カタログのスペクトル型は様々な文献からの寄せ集めなので 精度はまちまちである。カタログからは HIP, π(mas), πσ ICDS RA と Dec を取り込んだ。 π/πσ π/πσ > 10 の星の視差を使う。これは 100 pc 以内に相当する。それ以外の星に対しては測光距離を採用した。図５に 示すように、測光距離の誤差分布は視差距離とにていて、距離による変化もない。 1 kpc 以遠は外す また、1 kpc 以遠は外す。グールドベルトの最大半径は約 700 pc (Stothers, Frogel 1974, Westin 1985, Comeron et al 1994, Fernandez 2005) だからである。結局 553 星が残った。図６に投影プロットを示す。 |
  図６．サンプル星の投影プロット。 |
 表２．年齢ごとのグールドベルト平面パラメター。Westin 1985 より。 フィット結果 モデルを全サンプルおよび O1-B2, B3, B4, B5 の４サブサンプルに適用し た。どの場合も、かなりむらむらで銀河円盤に対しかなり傾いたグールドベル ト面と一様度が高い局所銀河面円盤で上手く合わせられた。 アウトライヤー 約 100/554 = 20 % はどちらの系にも属する確率が低かった。しかし、 光度分布関数をガウシアンにすると 10 % に下がった。 |
傾き 傾斜角は 14°±1° - 17°±0.3° であった。 ただし、最も若い O-B2 サンプルでは 16°±2° - 17° ±1° で幅が狭い。様々な研究で得られた傾き角は 14° - 22° に広がっている。 太陽高度 太陽の銀河中心面からの光度も得られた。サブサンプルごとに代わるが、 大体 Zo = 10 - 19 pc である。 投影分布 図７にはO-B2 サブサンプルと O-B6 全サンプルの XZ, YZ 投影分布が 示されている。グールドベルトの勾配が XZ 図に良く現れている。 図８の XY 分布を見ると、グールドベルト天体のムラムラな分布がよく分 かる。最も強い塊はオリオン領域にある。 |
|
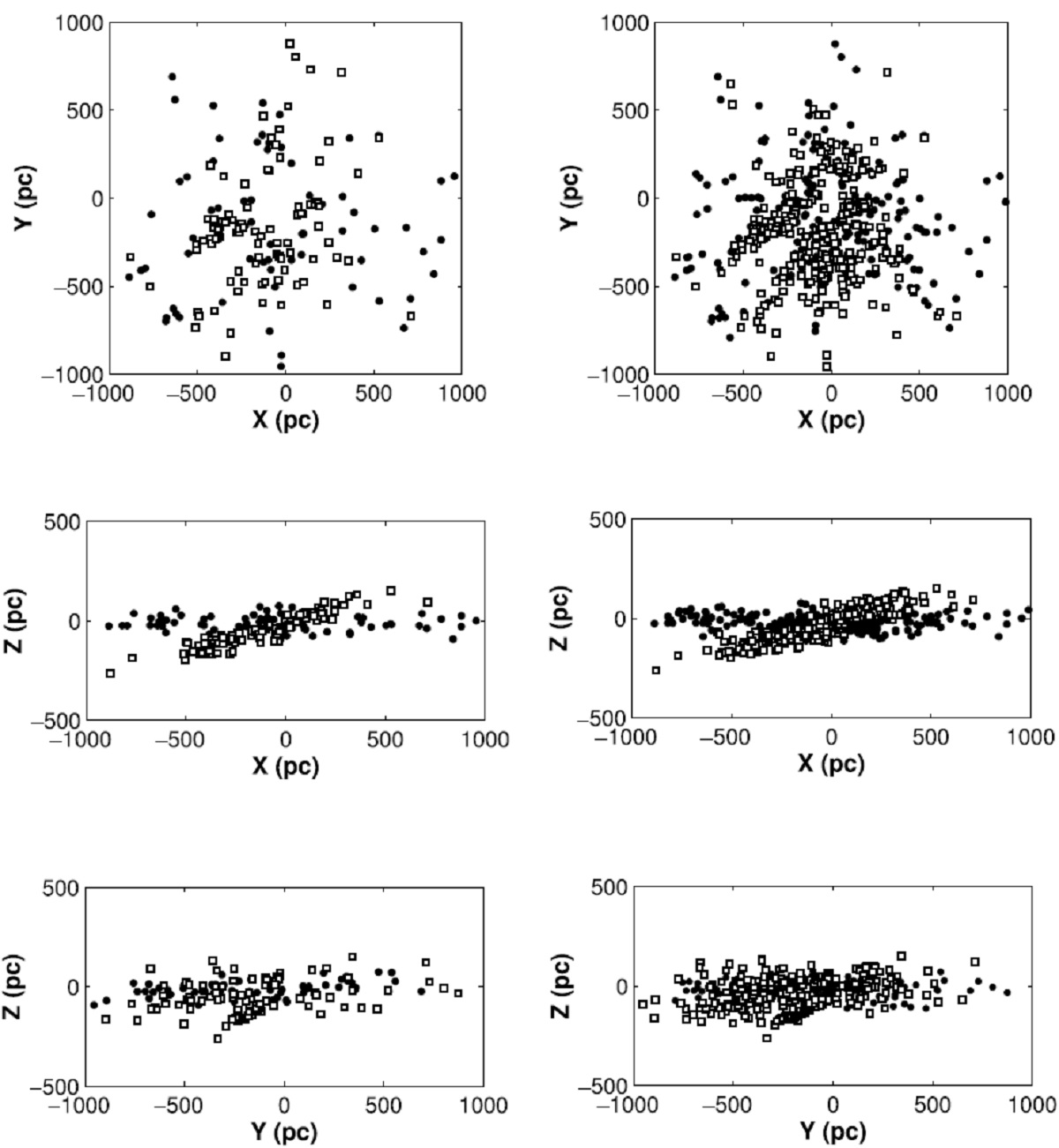
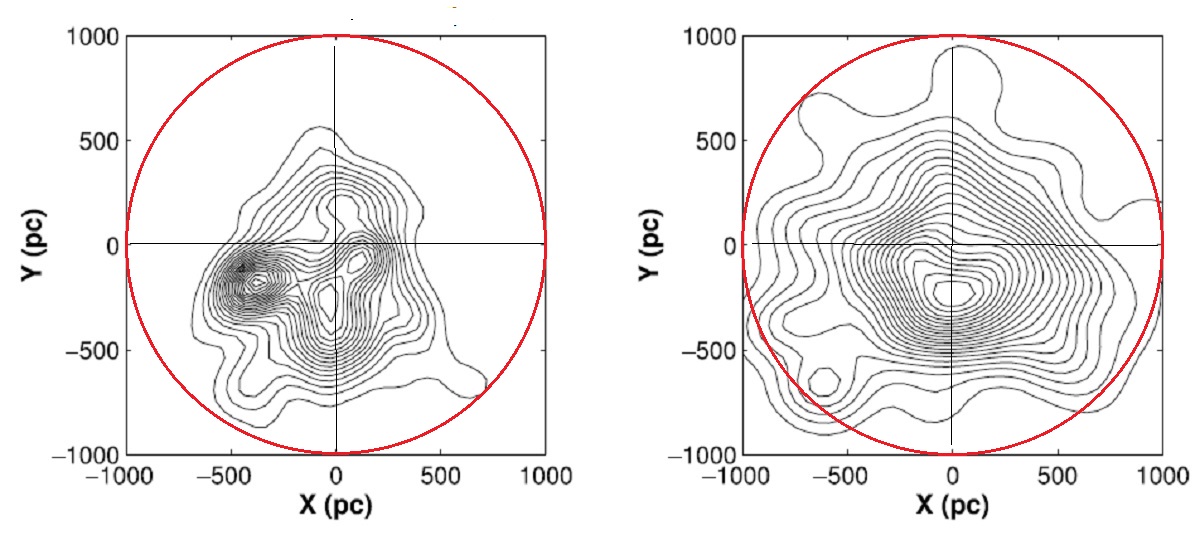
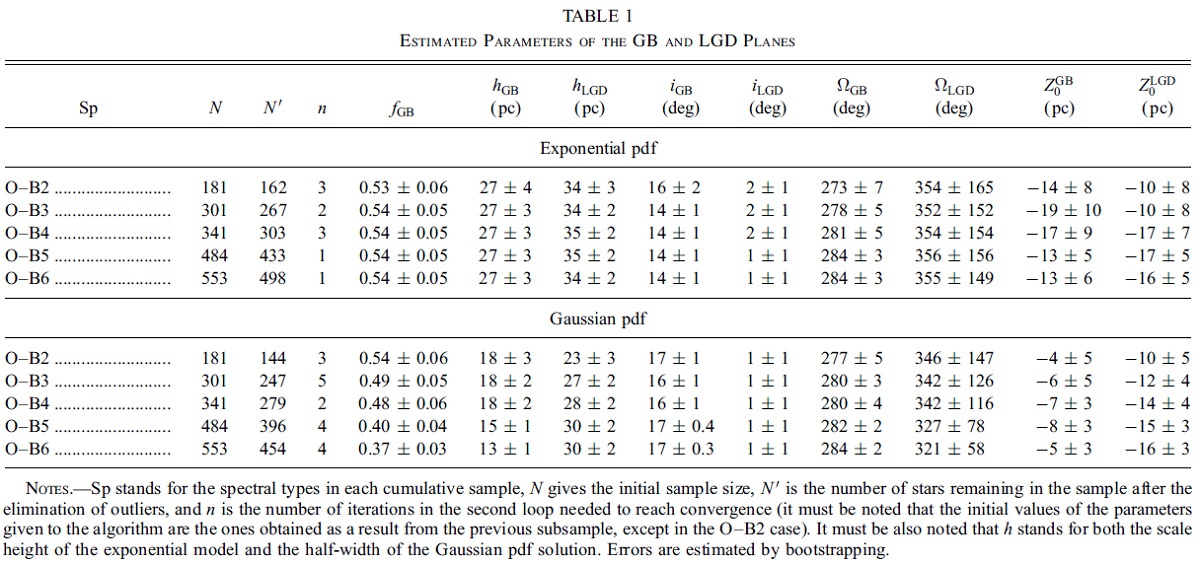
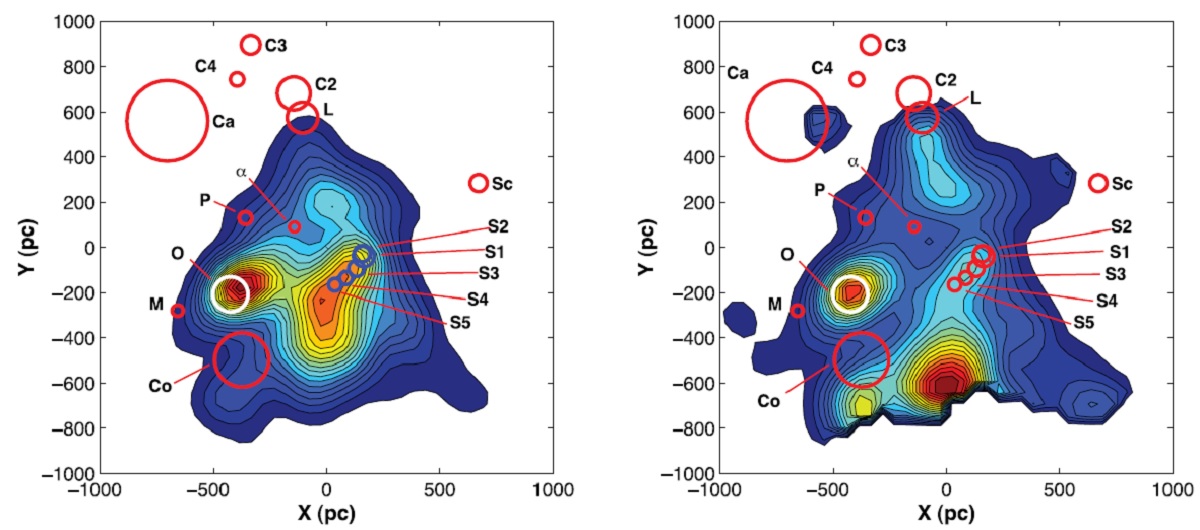
フラットフィールド LGD=局所銀河円盤の密度分布は距離と共に低下して行く。銀河円盤の密度分 布はもっと緩やかに変わる筈である。そこで、 LGD 成分の密度分布を一種の 「フラットフィールド」として利用して、GB = グールドベルトの密度補正を 行った。 星間減光 ただ、忘れていけないのは星間減光の効果で、これは LGD と GB とでは 別々に働く。従って、フラットフィールド法はあくまで一次の補正であり、 最終的な補正ではない。ただ、Poppel 1997 によるとこの方法で大丈夫らしい。 ５．１．モデルパラメターGD/LGD だけでも相対的な GB 密度分布を得ることはできる。しかし、 もっと進んで、個々の星に完全性補正の重み＝単に LGD の逆数、をつけて、 最前の逐次近似を繰り返した。得られた結果は表１とほぼ同じであった。 ５．２．空間構造中央ピークの消失図９には近傍アソシエイションをプロットした。完全性補正の結果、 中央ピークは消失し、スコルピオ領域が独自の集団として現れた。オリオン のピークは Ori OB1 位置へと移動した。 完全性補正は初めて 強調したいのはサンプルの不完全性を完全性補正した解析は今回が最初という ことである。しかし、空間パラメターに大きな変化はなかった。 |
５．３．アソシエイションGB 境界内とと外Blaauw 1965 以来、若いアソシエイション Sco-Cen, Per OB2, Ori OB2 が GB の一部を成すことは知られていた。GB のフィールド星は古いアソシエイシ ョンが破壊された結果の産物と考えられる。実際上の３集団は GB の典型的な 半径の内側にある。しかし, 太陽から 1 kpc 以内にあるアソシエイションは 大部分がGBの古典的境界の外に位置する。 新しい塊 フラットフィールディング補正の後の密度分布（図９右）を見ると、新しい 固まりが出現したことが分かる。これらの塊りは既知のアソシエイション （de Zeeuw et al 1999）に対応する。アソシエイションが GB に属するかど うかは、単にその位置だけでなく、密度ピークがアソシエイション位置と一致 しなければいけない。こうして、 Cam OB1m Lac OB1, Col 121 それに、 (ZX, Y) = (0, -600) 付近の塊りが GB を拡大することになった。最後の 固まりは Vela rift に繋がると思われる。 Vela グループ 最も驚くべき結果は Vela group が GB に属することである。 レフェリーは GB と LGD が異なる減光を受けているための偽効果でこの塊 が生じたのではないかと述べた。しかし、塊は GB と LGD との交差域に あり、減光が異なる効果は小さい。 |
|
３次元分類法 新しい３次元分類法により、GB と LGD の構造を明らかにした。 この方法は GB 空間分布の構造を調べるのに適している。 ベルトの構造パラメター ベルト幾何学パラメターを決めた。 |
完全性補正 完全性補正を施した結果、偽りの副構造を除き、真の構造を強めた。 |