The distances and distribution of planetary nebulae

２．観測減光の決定　

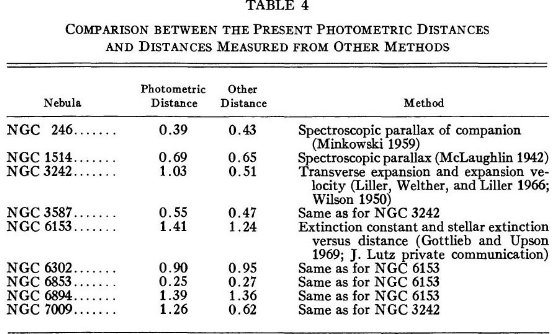
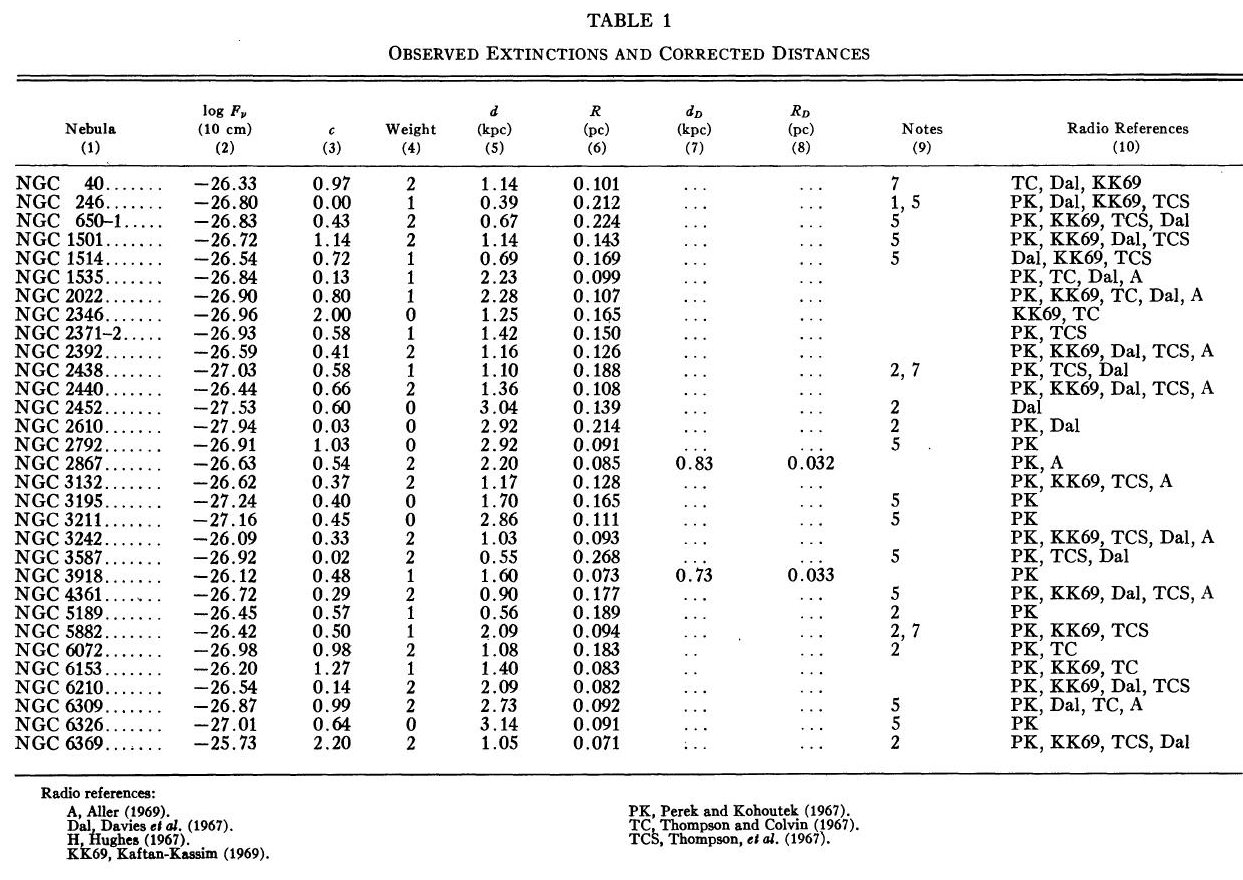
減光 c　 二つの c 決定法　 　最良の減光データは、パッシェンライン対バルマーラインの比か電波フリーフリー 連続光対 Hβラインの比から得られる。理論値は電子温度に対して決められ、その 値からのずれは星間減光に帰せられる。 パッシェンとバルマー線による ｃ の決定　 　明るい星雲のパッシェンラインの観測は主に O'Dell 1963 により行われた。減光 定数 c は、Hβ 線における対数減光量で、次の式で与えられる。 c = 1 [ log ( P ) - log ( P ) ] 　　　(1) Δ fλ B O B C ここに、(P/B)Oは観測されたパッシェンとバルマーの強度比、(P/B) Cは Baker-Menzel Bタイプモデルでの理論値である。Δ f λは赤化関数のパッシェン線とバルマー線とでの値の差である。 計算では T = 5000K が仮定された。表１の第３列には減光定数Ｃが載せてある。 電波フリーフリー放射と Hβ線からの ｃ の決定　 もっと多くの星雲では、フリーフリー放射を使って、ｃを求める。フリーフリー の体積放射率 εω は式（２）にある。（省略） 　一方、Hβ の体積放射率 ε(Hβ) は 　　　　　　　4πε(Hβ) = Ni Ne α(Hβ)hν(Hβ) 　　　　　　　　(3) ここに、 α(Hβ)は Hβ 線の有効再結合係数である。式（２）、（３） から、光学的に薄い電波フリーフリーと Hβ 線のフラックスの比、[Fνdν/ Fc(Hβ)]が式（４）として書ける。 Fνdν = 9.210×10-27 ln 49.62 Te3/2 [ 1+ N(He+) FC(Hβ) α(Hβ)Te3/2 ν N(H+) +4 N(He++) ln(24.81Te3/2/ν) ] 　　　(4) N(H+) ln(49.62Te3/2/ν) ここにFc(Hβ) は真の（減光を受けない）Hβ のフラックスである。減光定数 c は、 c = log (Fνdν)o - log Fνdν 　　　　　　(5) FO(Hβ) FC(Hβ) ここに右辺の第１項は観測値、第２項は減光ゼロでの理論値である。 電波観測データと Hβ フラックスデータ　 　フリーフリーの観測には波長 10 cm を標準波長にする。この波長は、光学的 厚さと広い観測可能性との両立から選ばれた。表面輝度の高い星雲の多くが 10 cm では光学的に厚い。しかし、それらの星雲はパッシェン・バルマー線の 観測があるので大丈夫である。 　観測の第１ステップは出来るだけ多くの星雲の電波スペクトルを得ることである。 このため、Parek, Kohoutek の惑星状星雲カタログを用いる。表１にはそれに いくつかを追加した。これらを眼視でつないでスペクトルを作り、波長 10 cm でのフラックスを決める。 　Hβ フラックスデータもParek, Kohoutek カタログから得た。 電子温度の謎＝「水素温度」 　理論式（４）の評価には電子温度が必要である。可視域禁制線の観測は 1000 - 1500 K を示唆する。しかし、ここ数年、水素の低励起再結合線の比から決めた 電子温度は禁制線温度の半分くらいになるという結果が出てきている。これらの 「水素温度」が物理的な温度なのか、再結合過程の理解不足によるものか結論 が出ていない。 　例として IC 418 を挙げると、バルマー連続光と Hβ との比から 4800 K, 電波連続線から 12,500 K である。O[III] からの温度は後者に近く、禁制線の 理論は信頼度が高いので電子温度としてはこちらが正しいであろう。

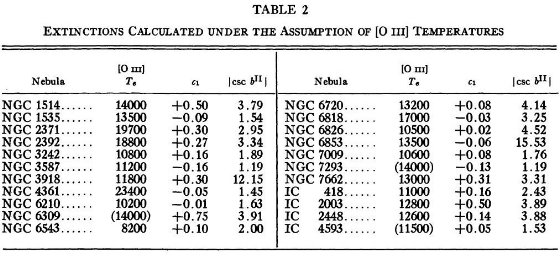
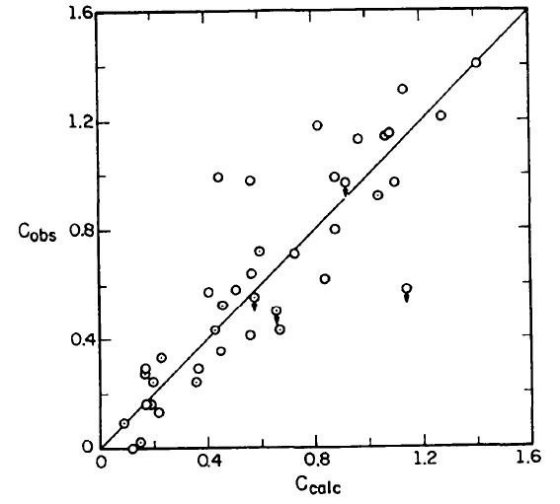
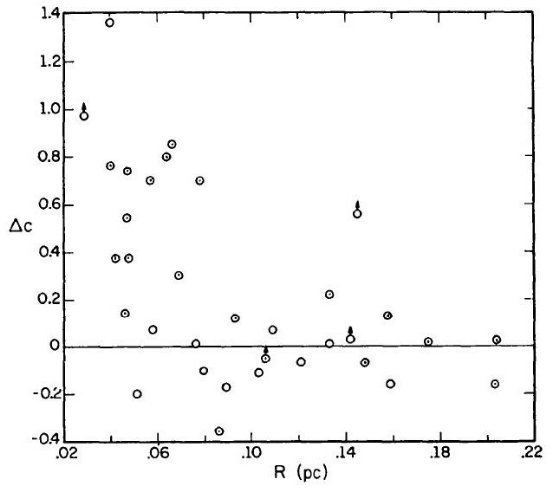
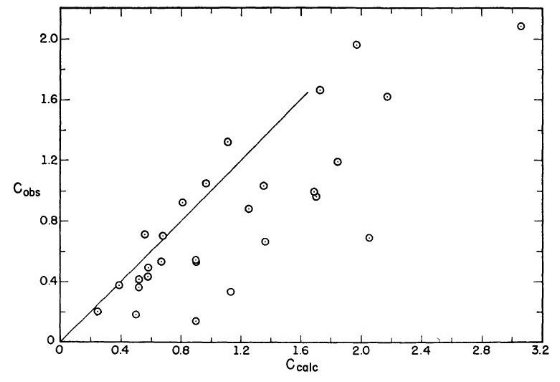
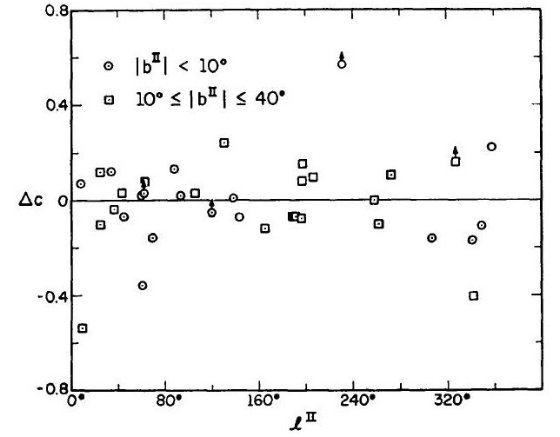
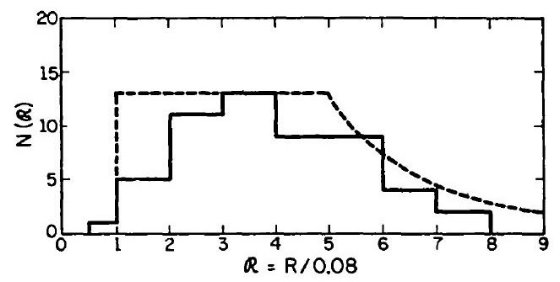
「水素温度」使用の正当性 　しかし、減光の導出に用いるのは再結合線の比である。したがって、減光定数の 式に入れるべきはこの比から導出される「温度」を用いる必要がある。この「温度」 は減光がない時の再結合線の比を正しく表わすのであるから。本論文では 「水素温度」＝ 5000 K を全ての星雲に適用する。 　図１は「水素温度」採用の妥当性を示すものである。上図は「電子温度」5000　K を用いて計算した減光量 c であり、下図は禁制線からの温度を用いて決めた減光量 c1 をプロットした。図中矢印は Arp 1965 の銀河計測から決めた 銀極方向減光量 0.2 等 である。上図は銀極減光量と合致するが、下図は受け入れ 難いほど低い減光量となり、極では負になってしまう。この c1 は 表２に載せてある。 　このように、物理的な温度として正しいかどうかは問題であるが、低い「水素 温度」は減光定数を決めるのには使える。バルマー連続と Hβ との比から きまるこの「水素温度」が電波と Hβ の比にも適切かどうかはっきりしない。 しかし、星雲の物理がもっとよく理解されるまでは、この方法を使うしかない。 それに、「禁制線温度」を採用してもその結果の距離への影響は 10 % 程度である。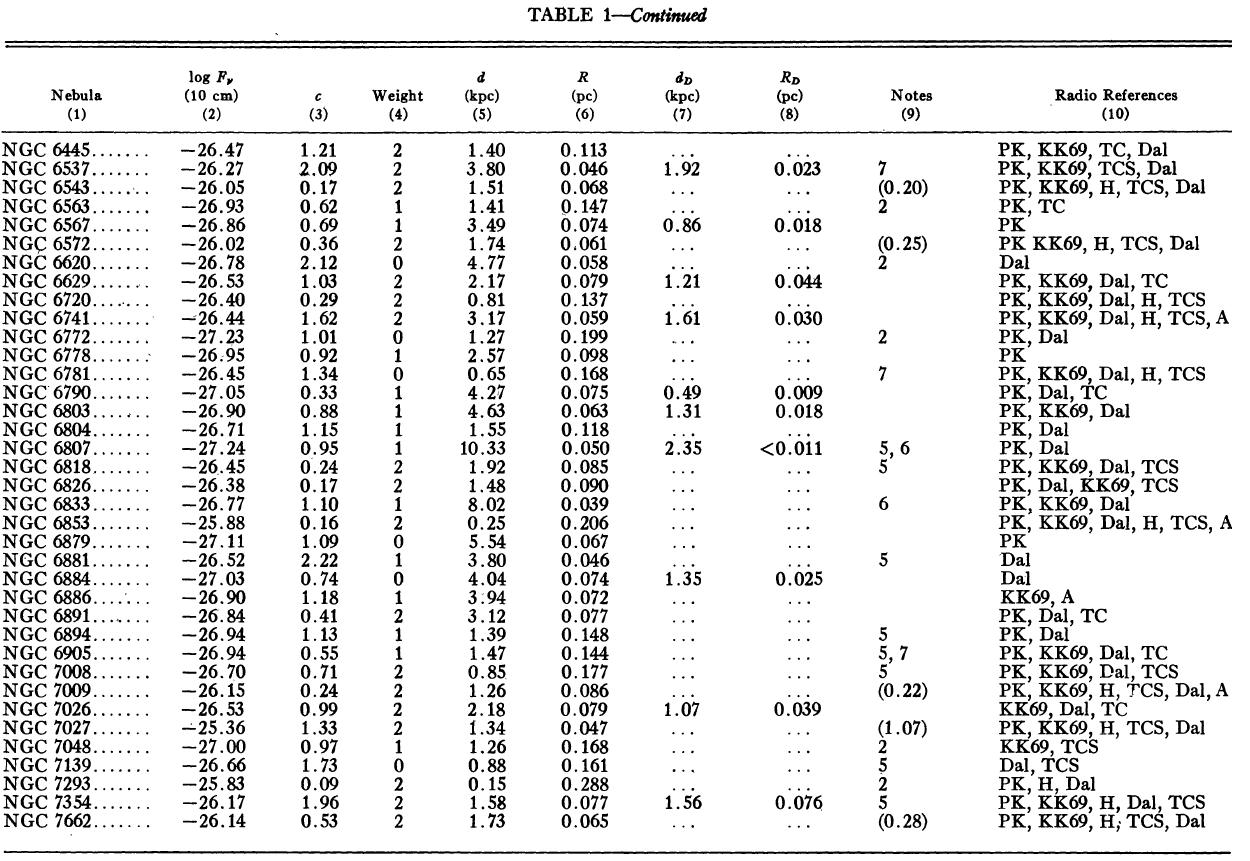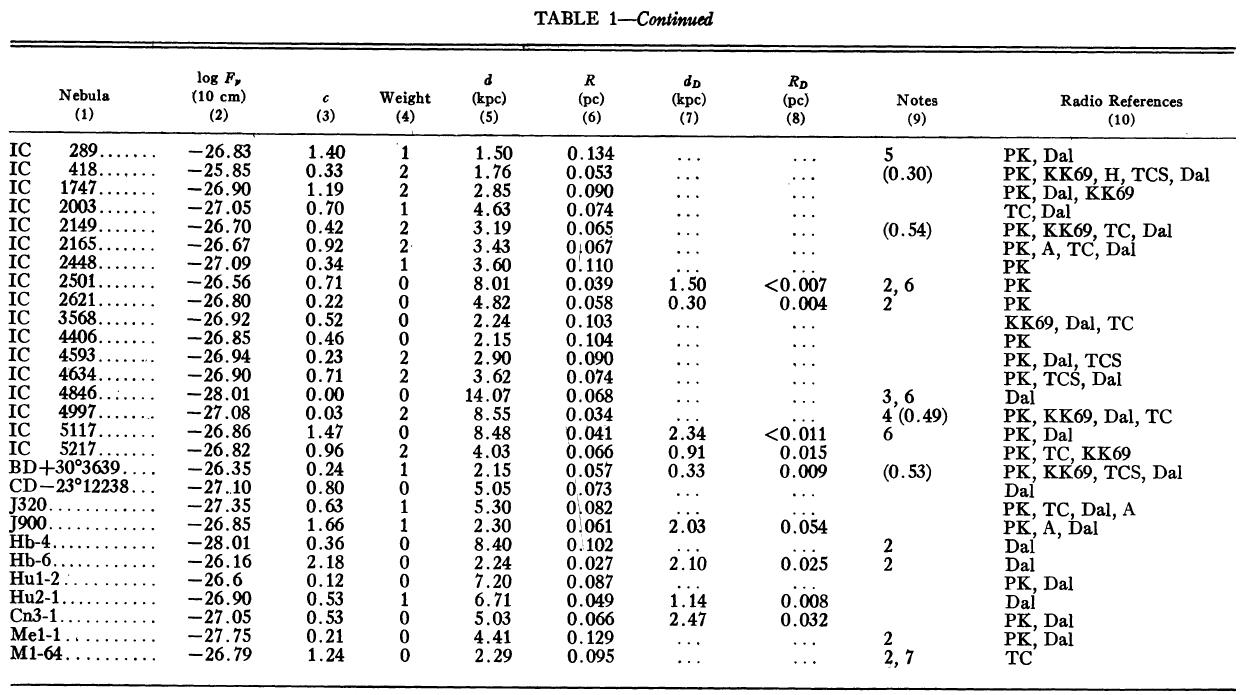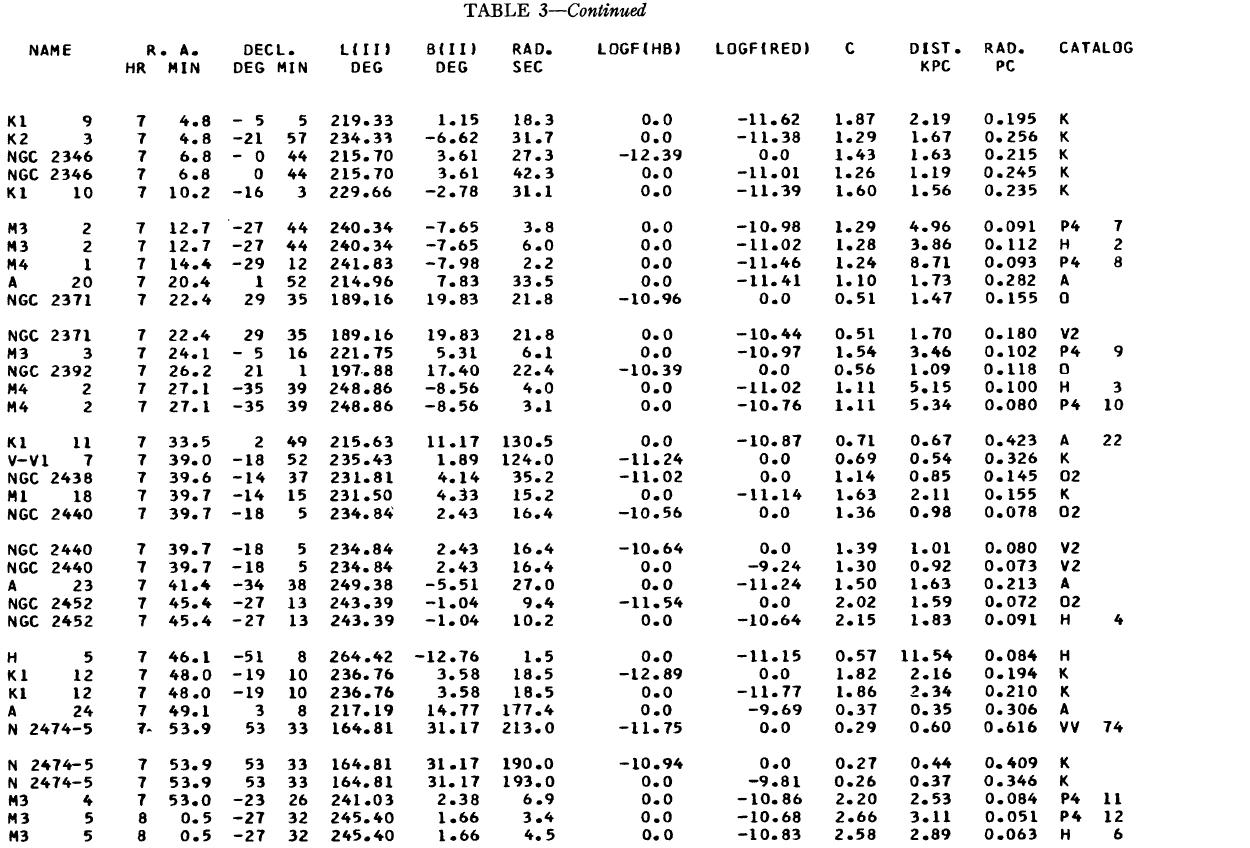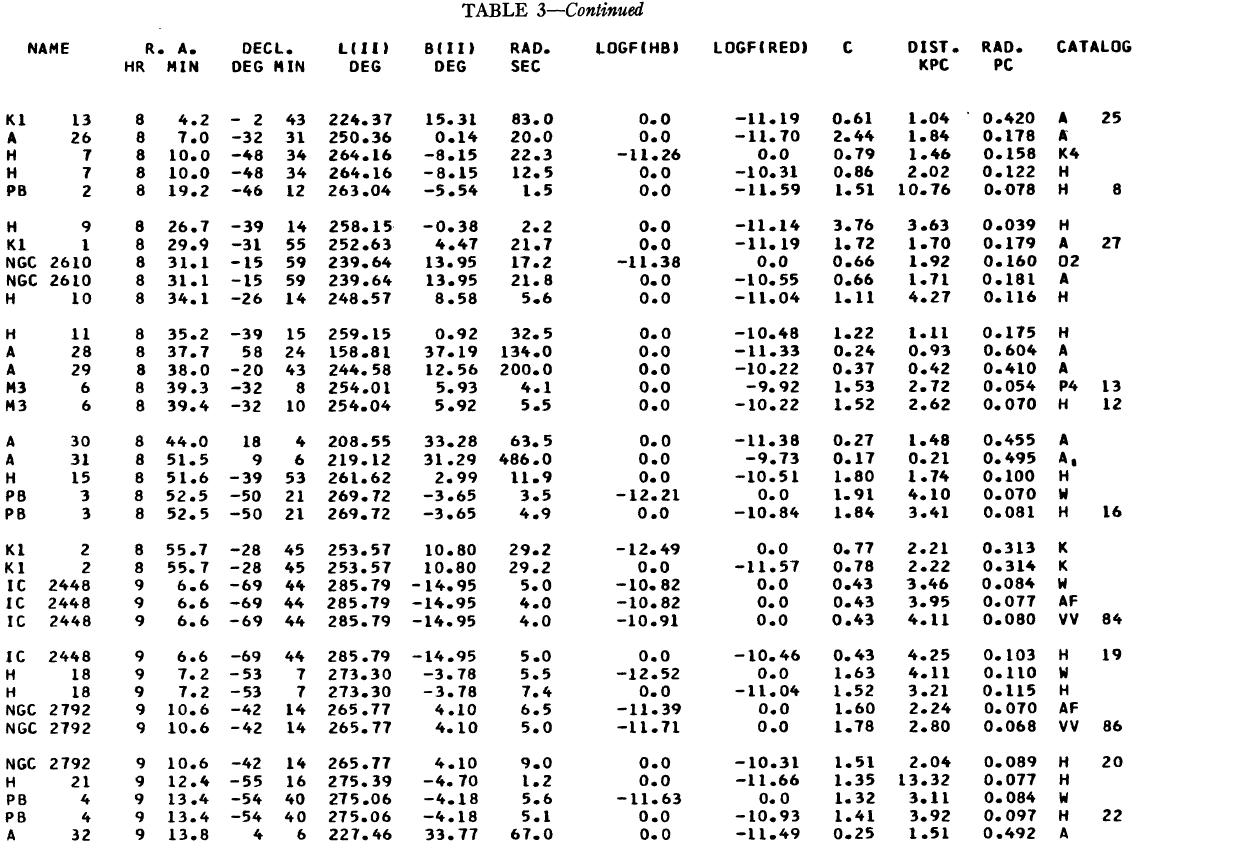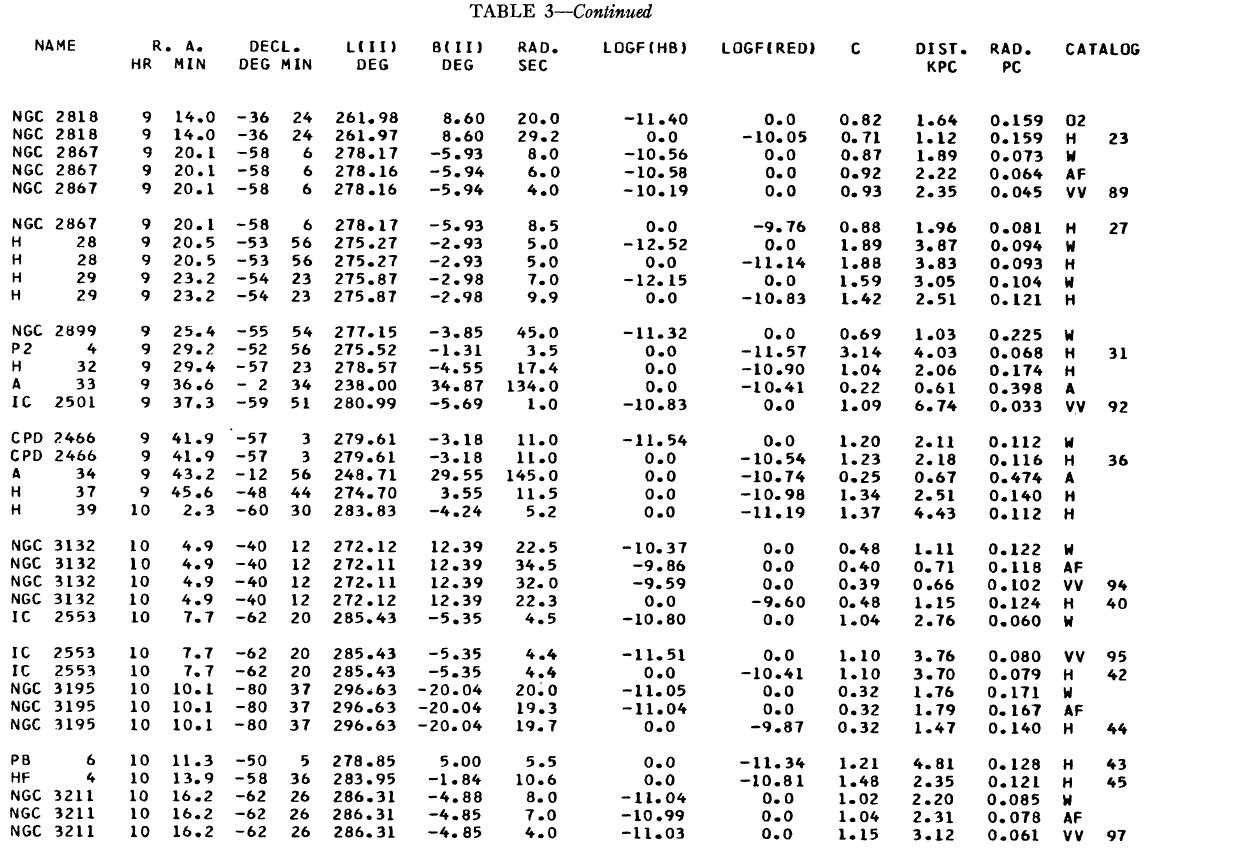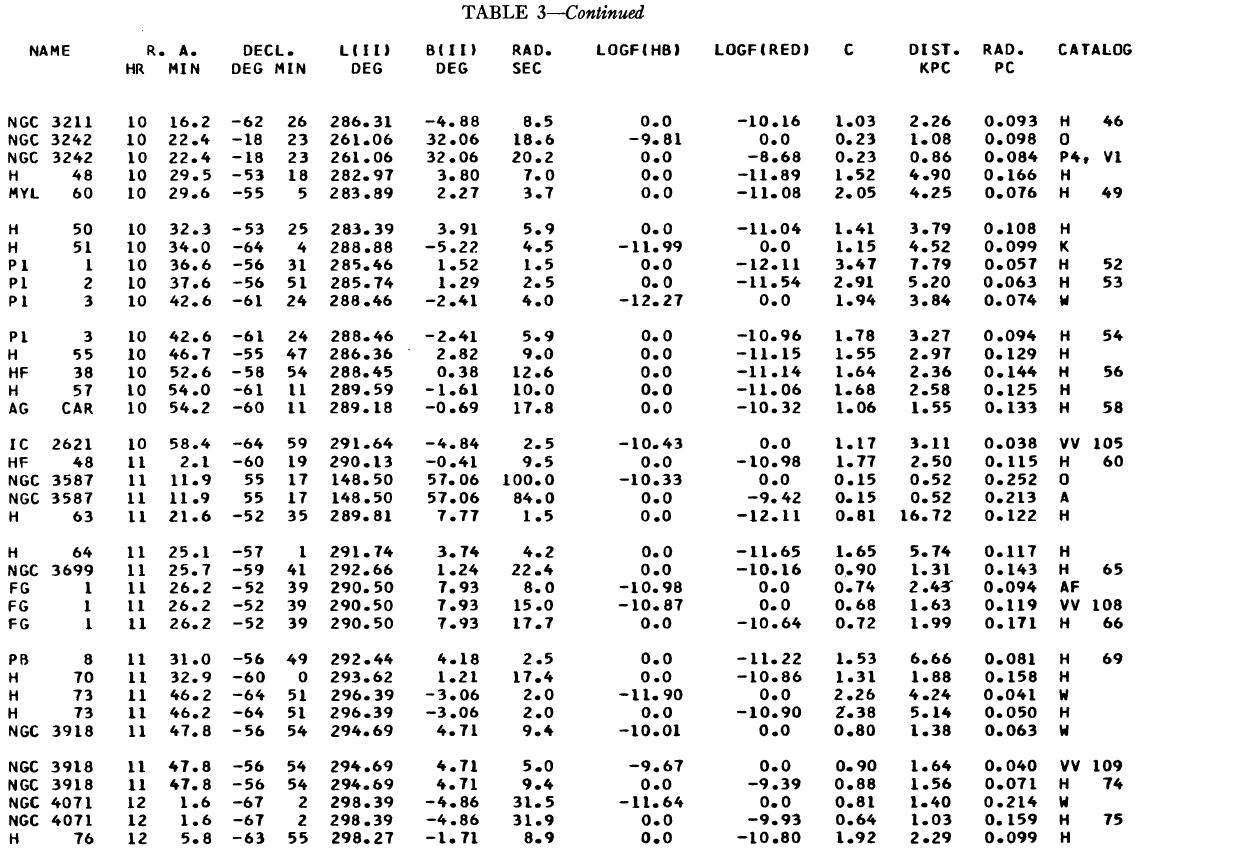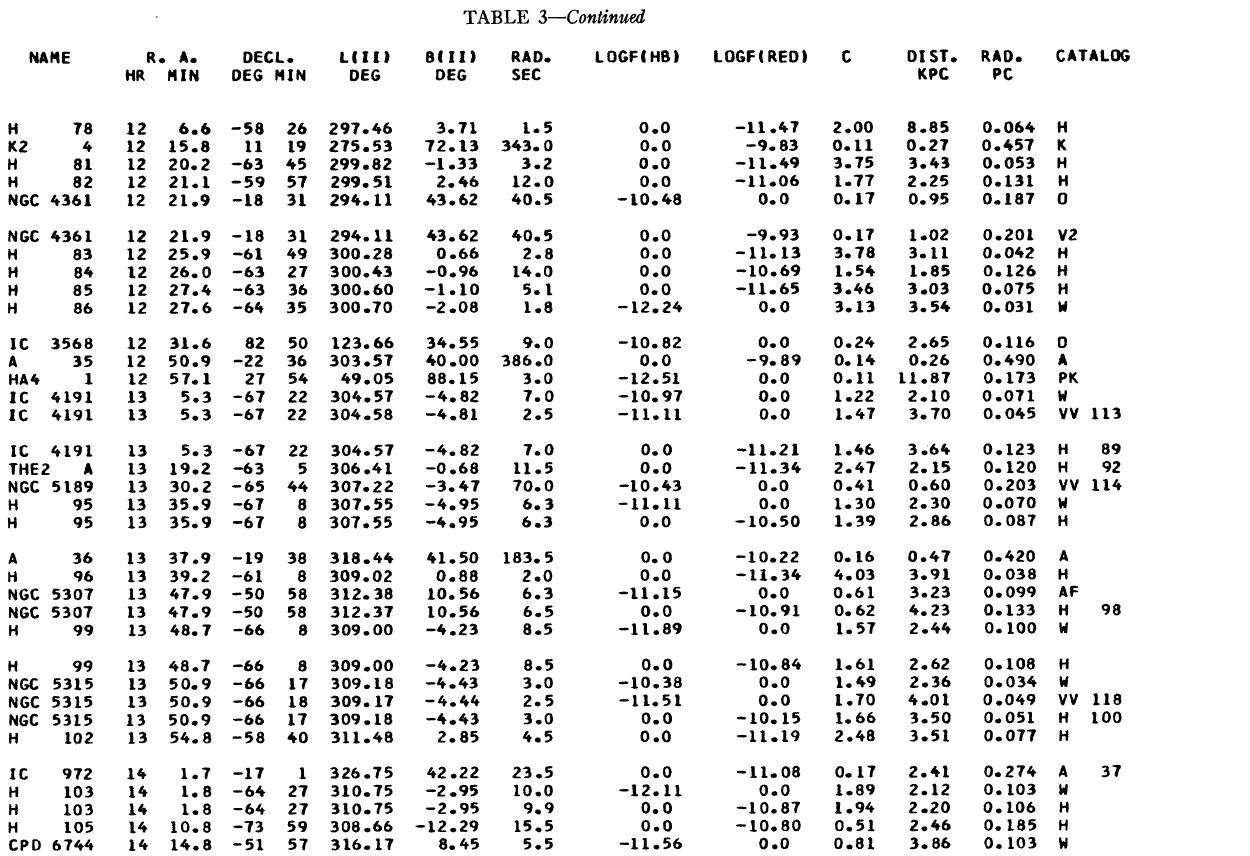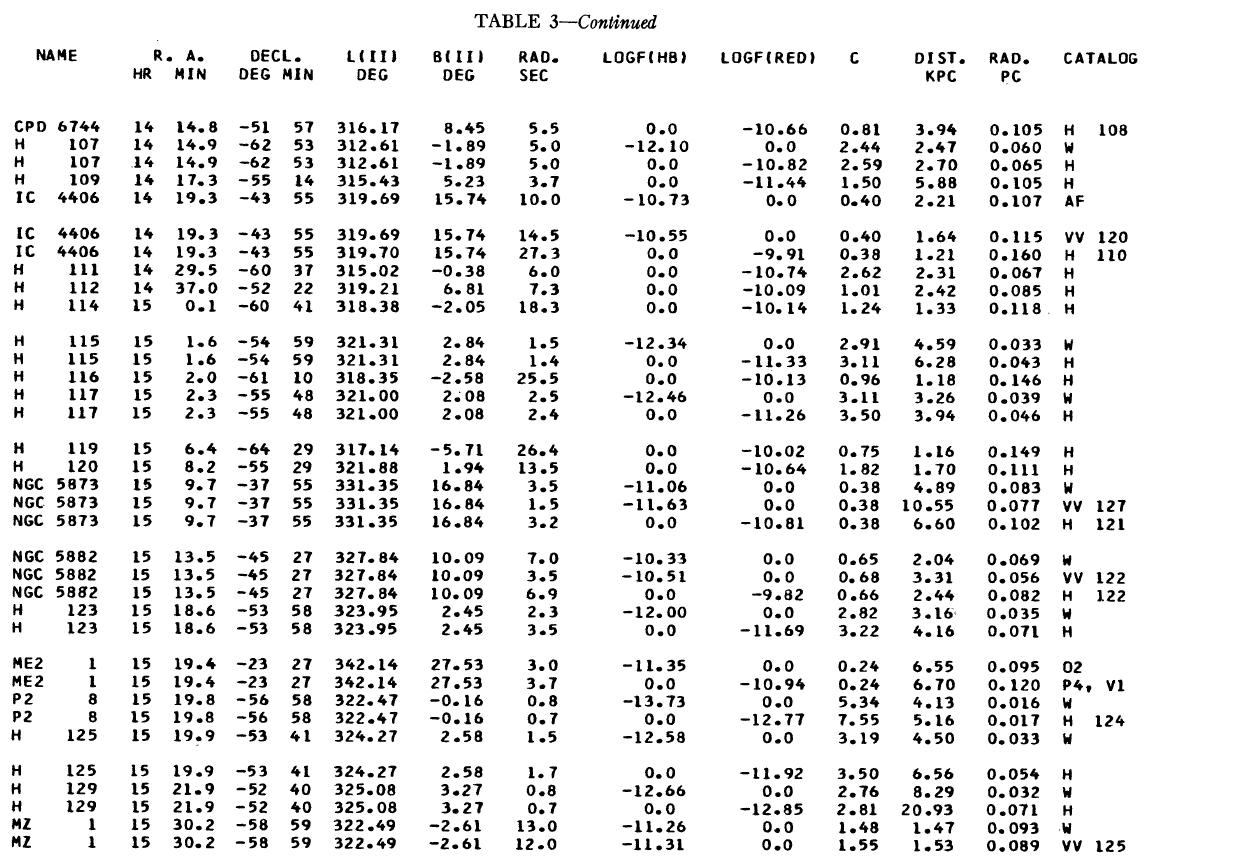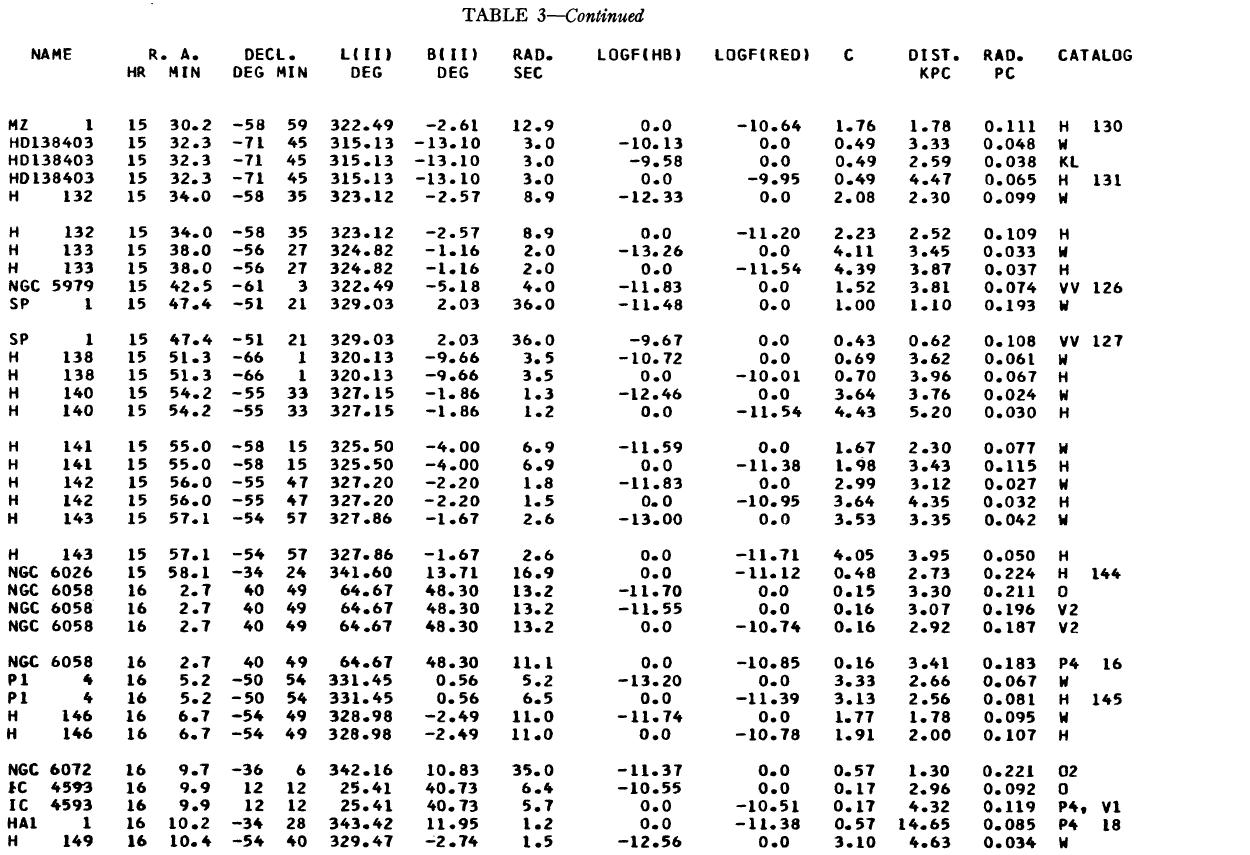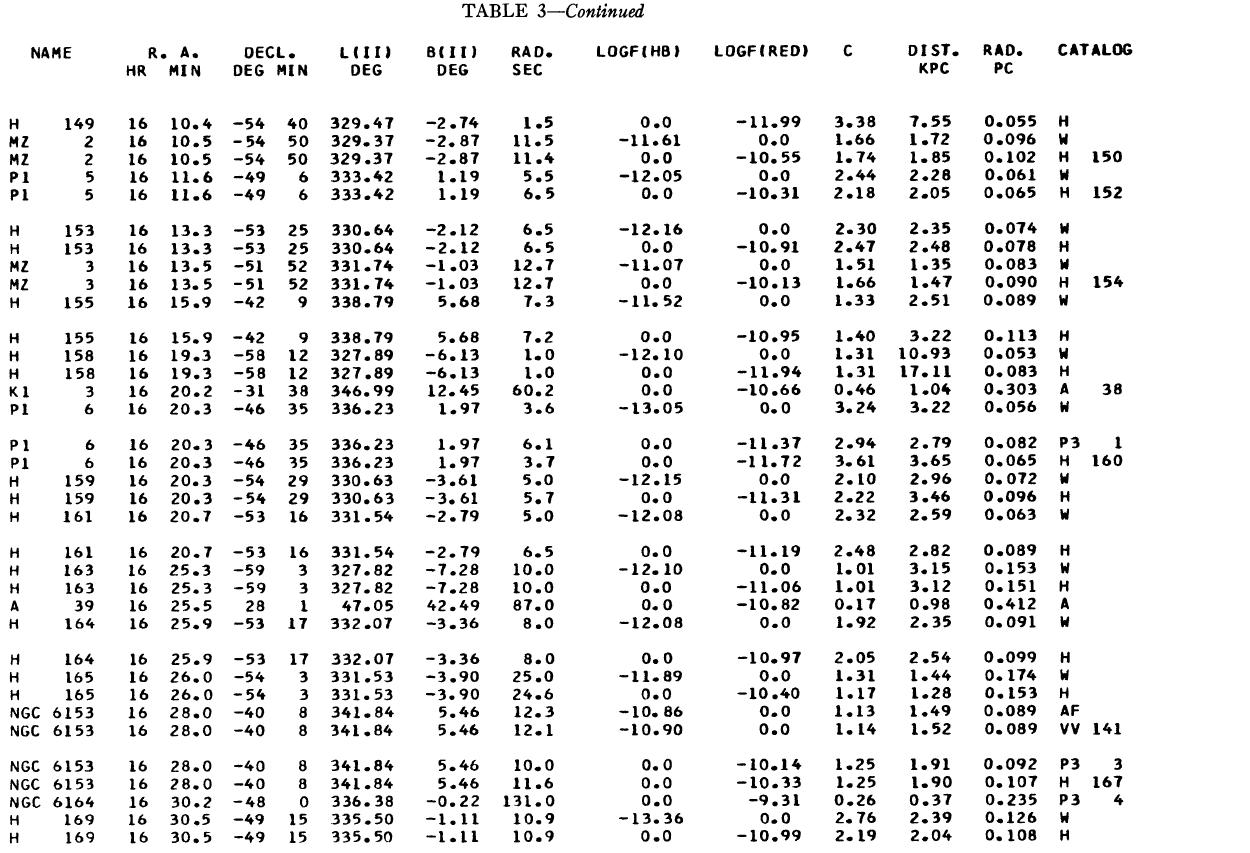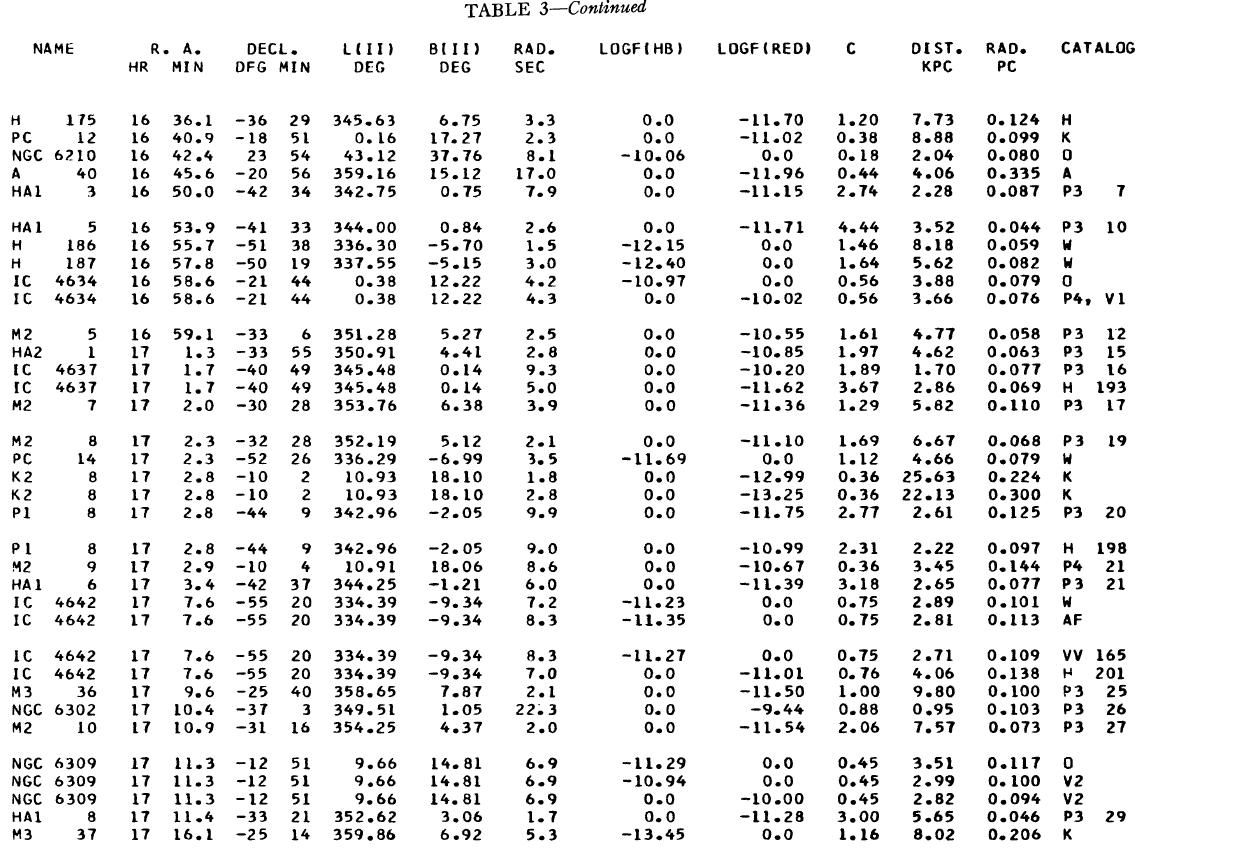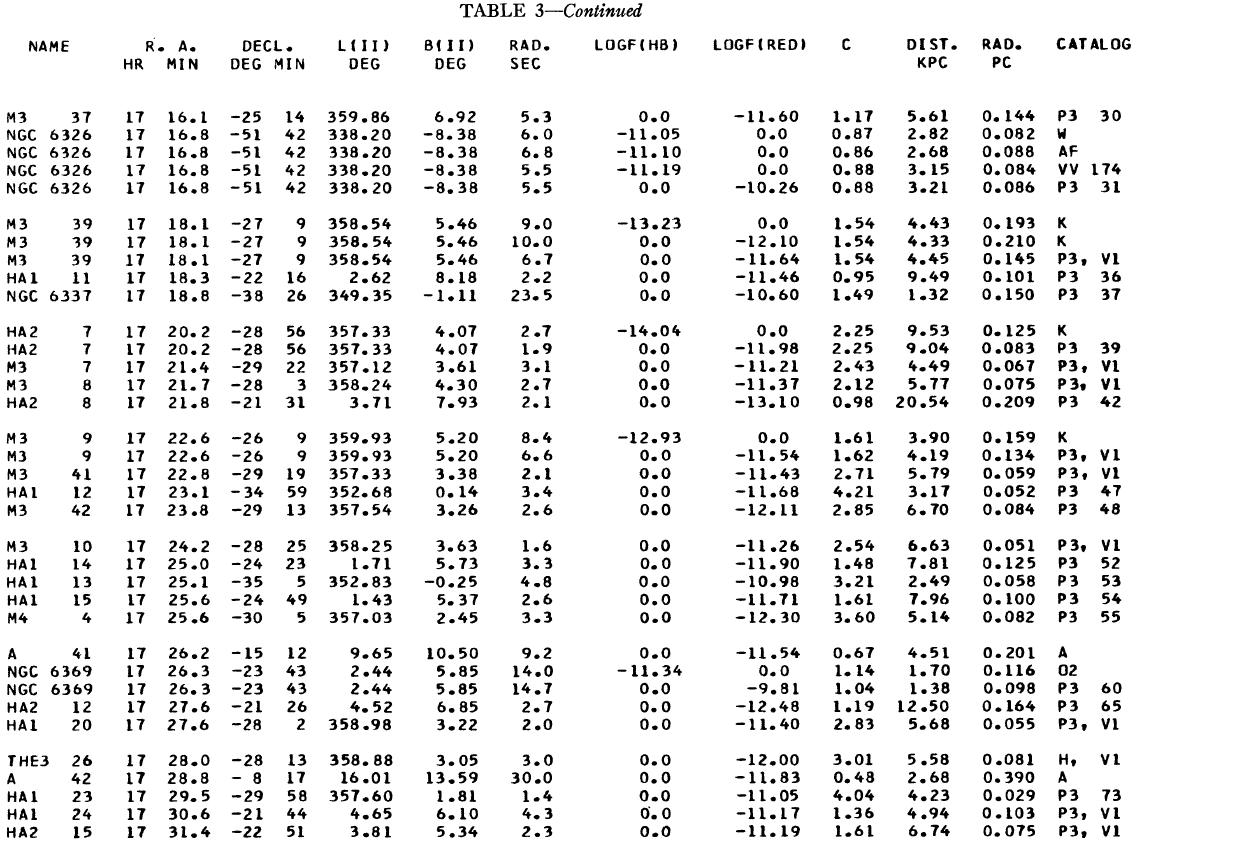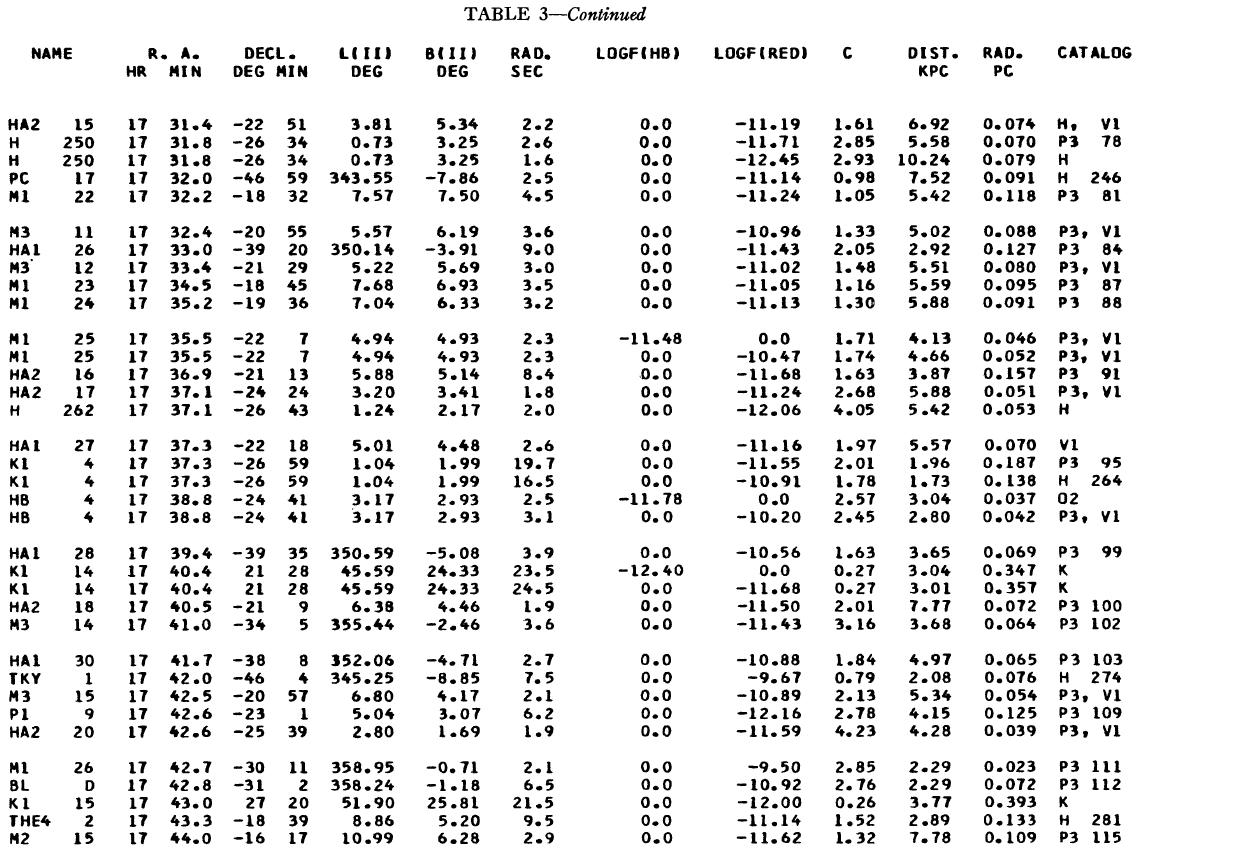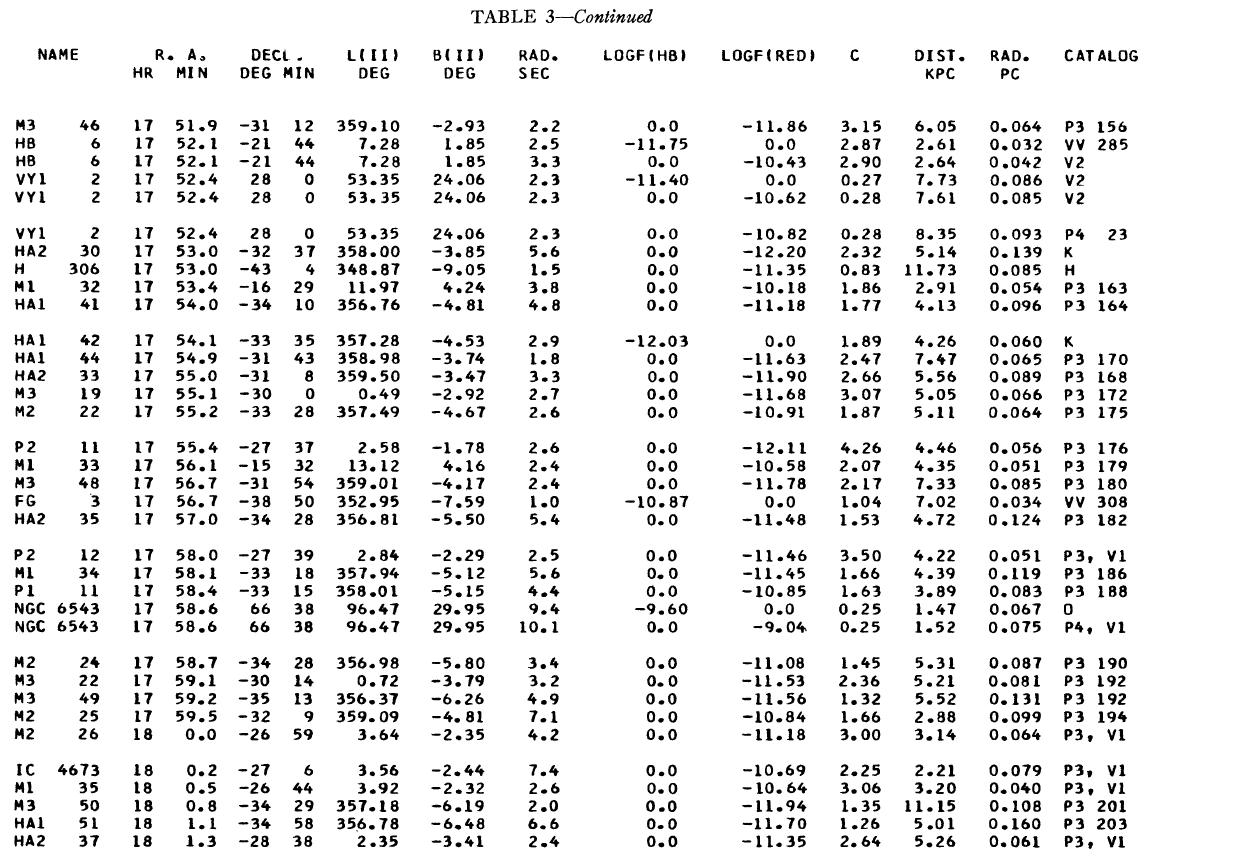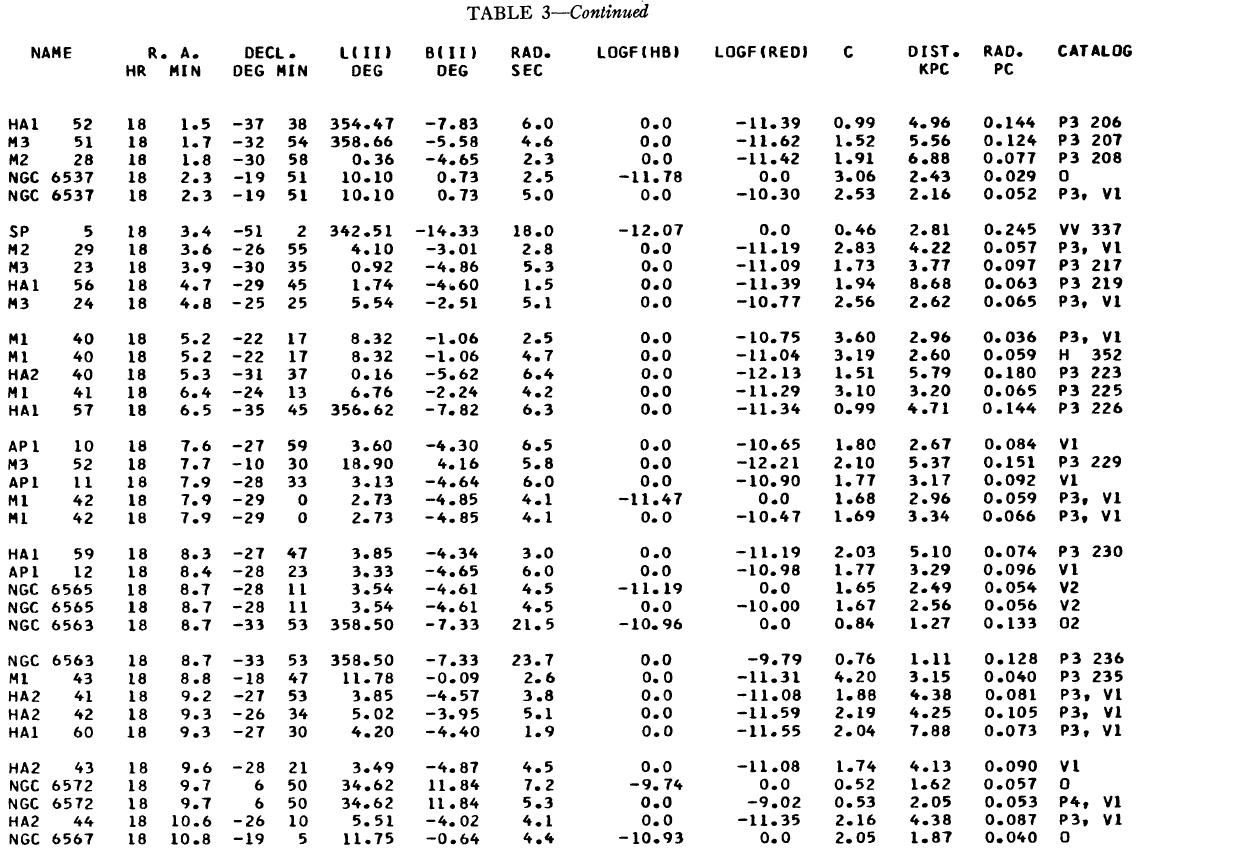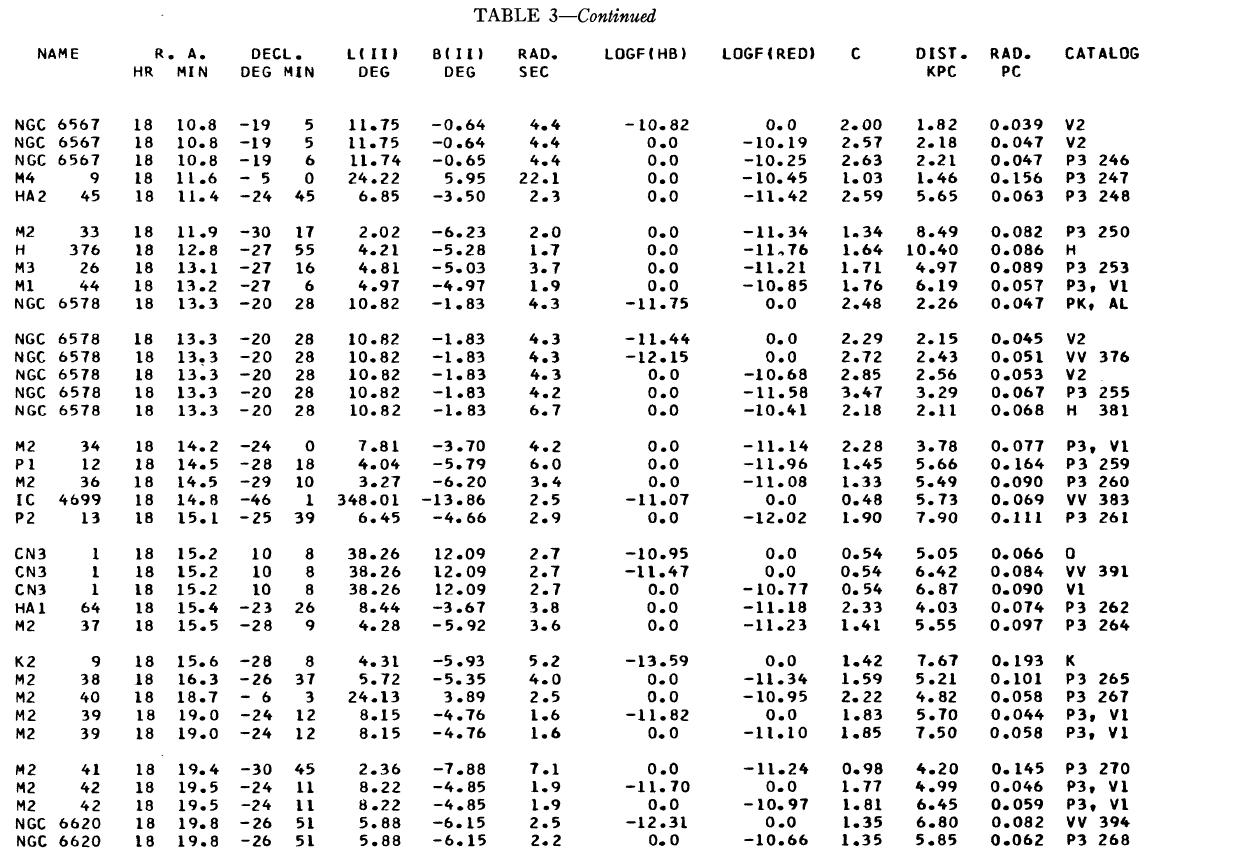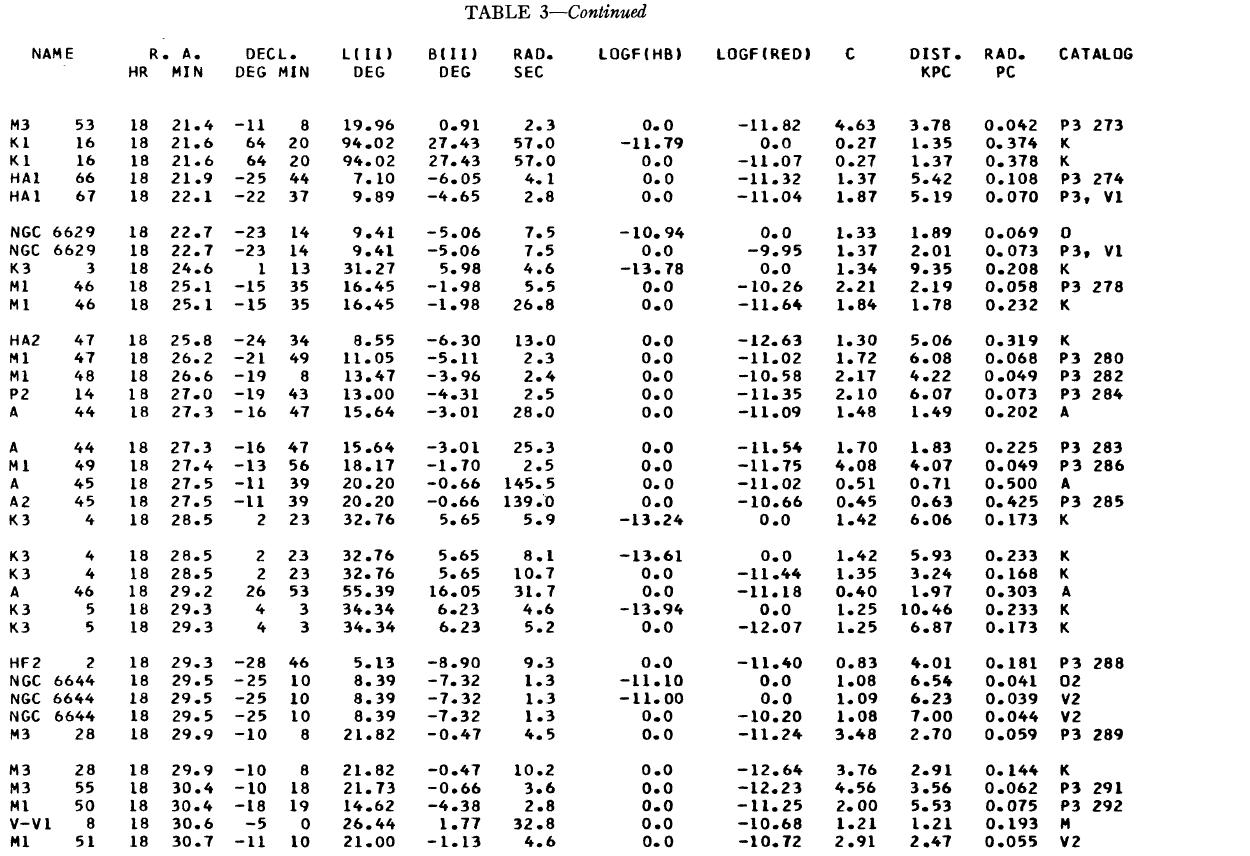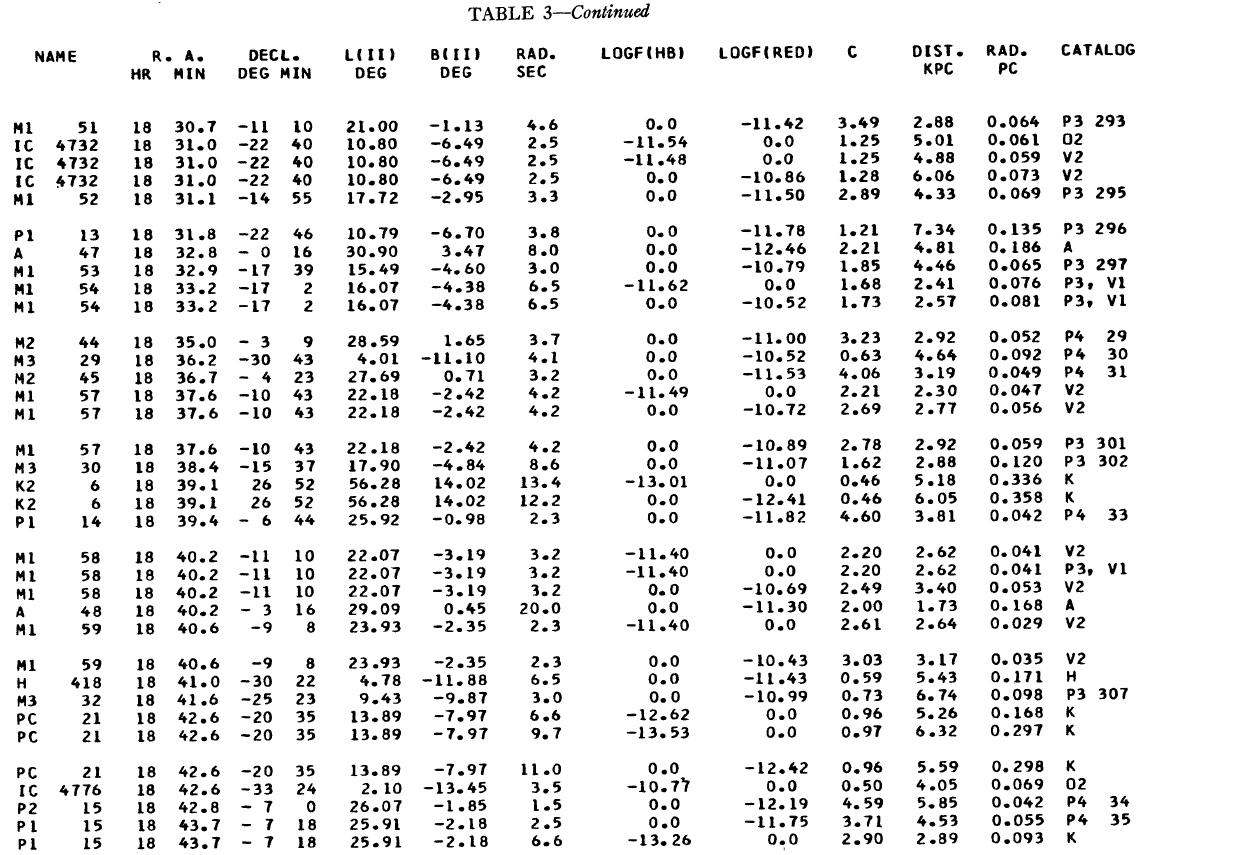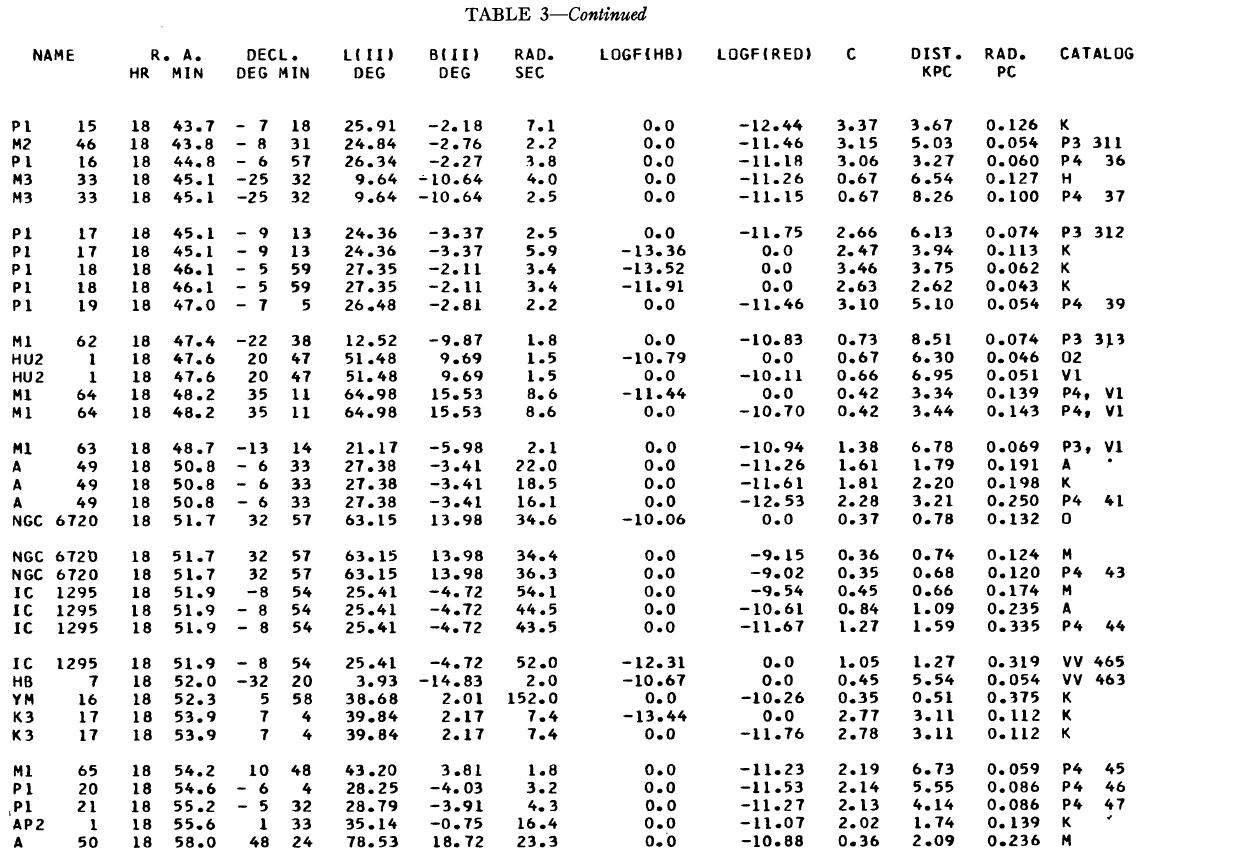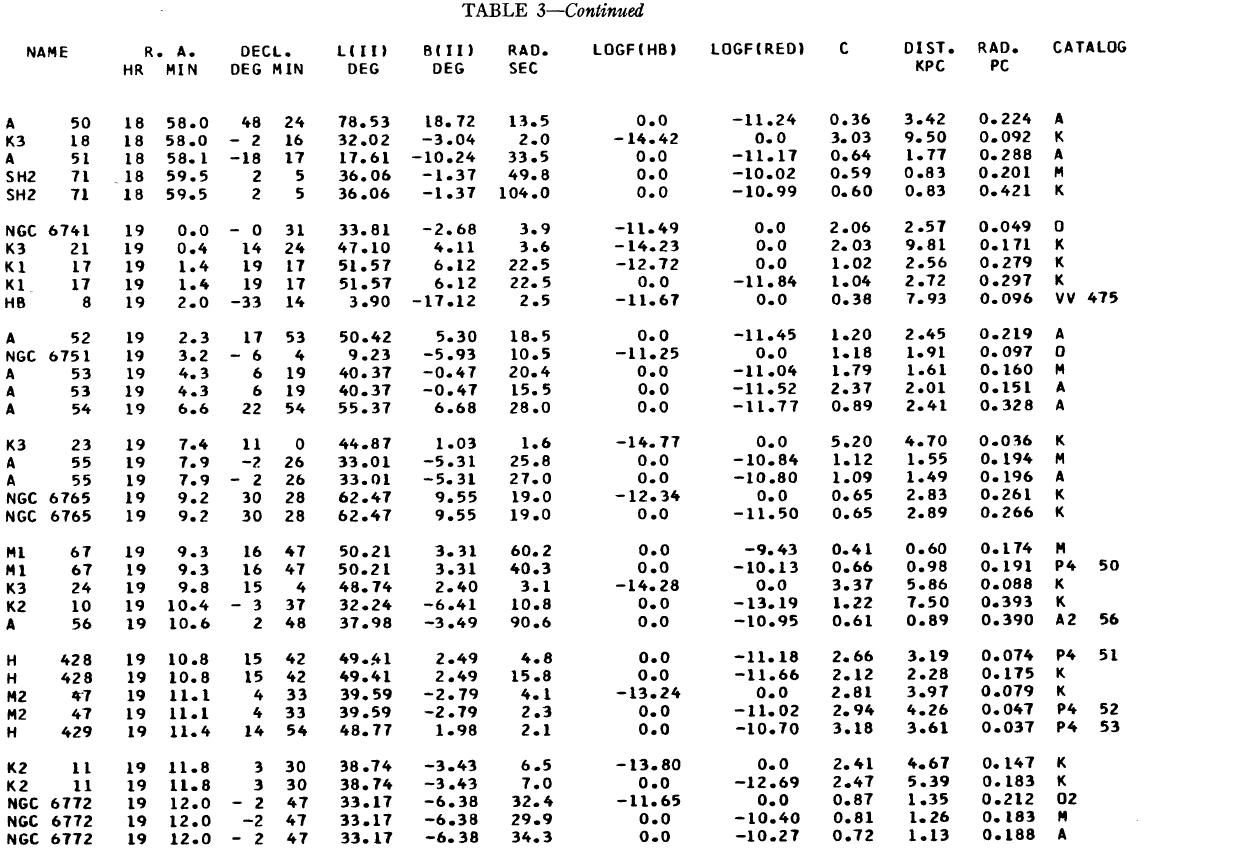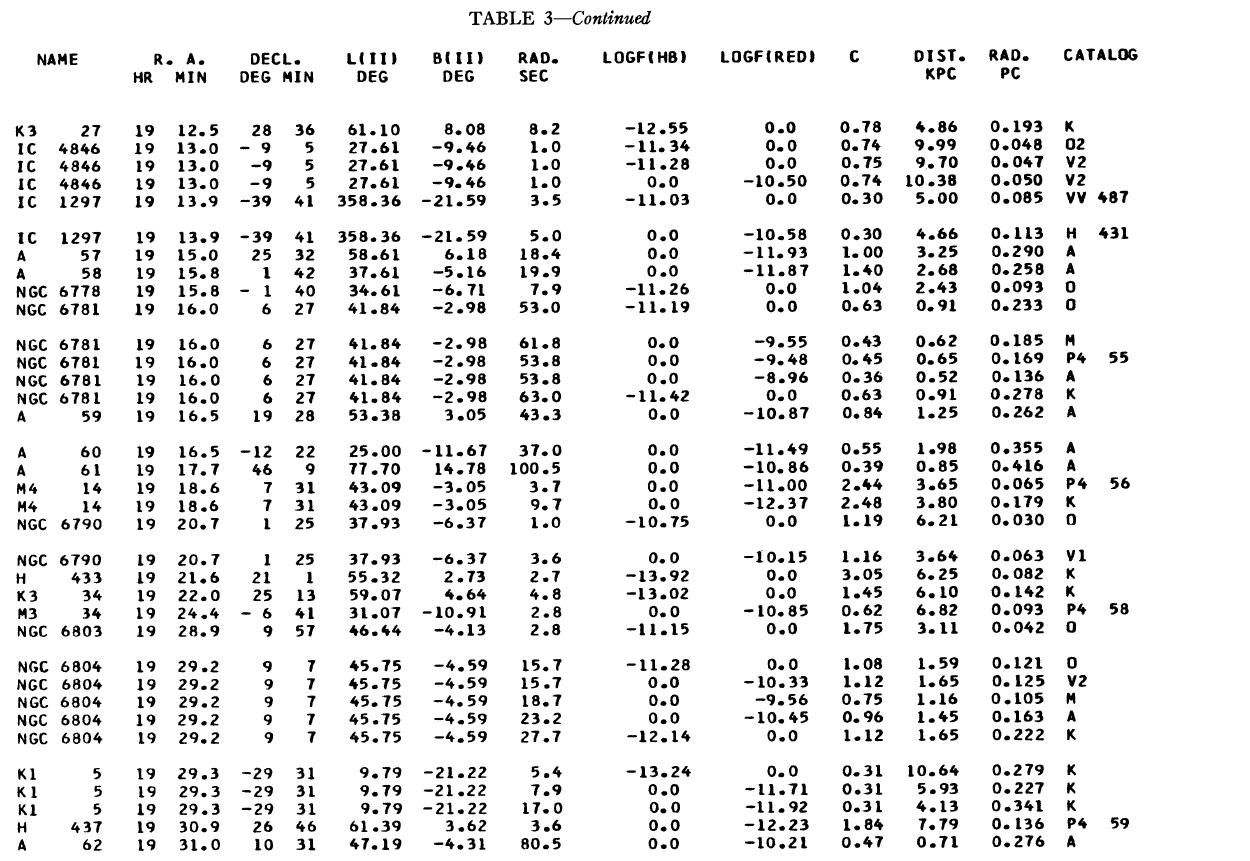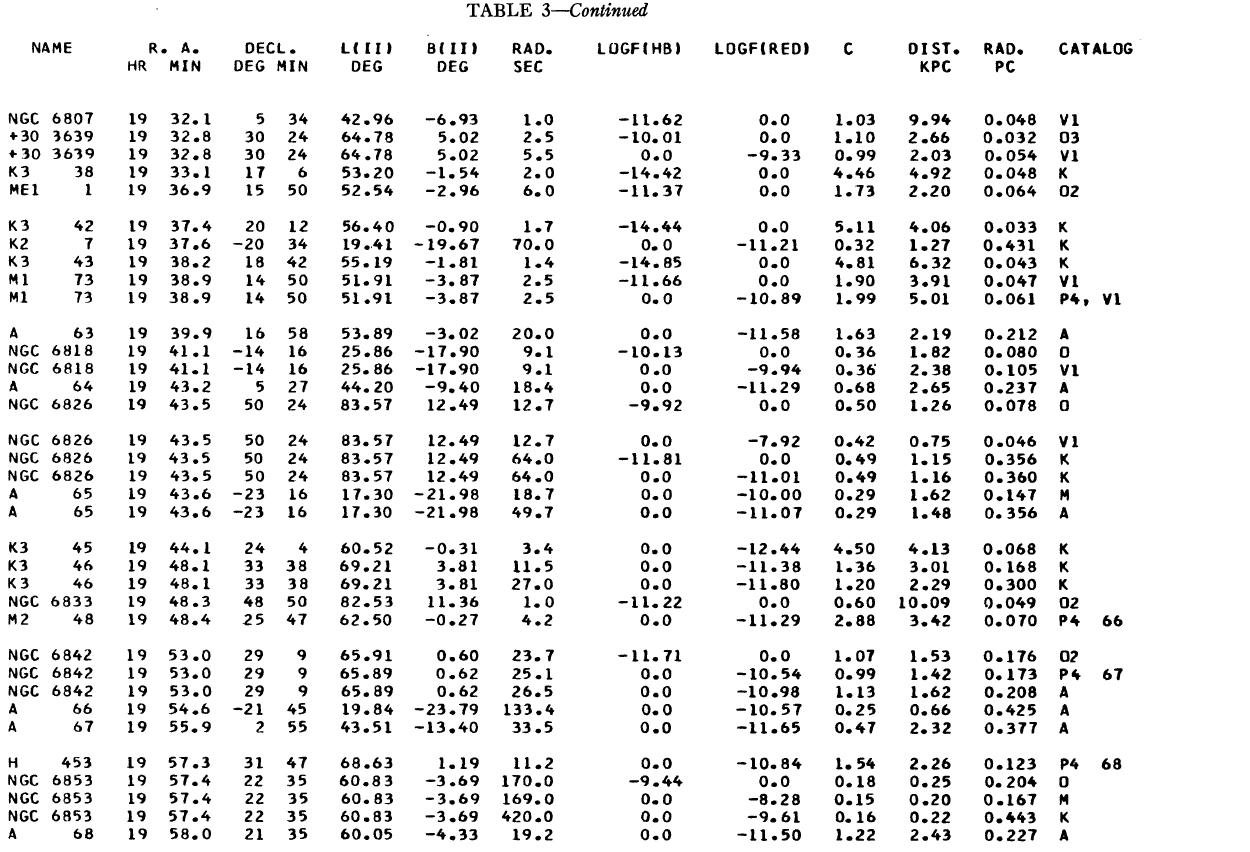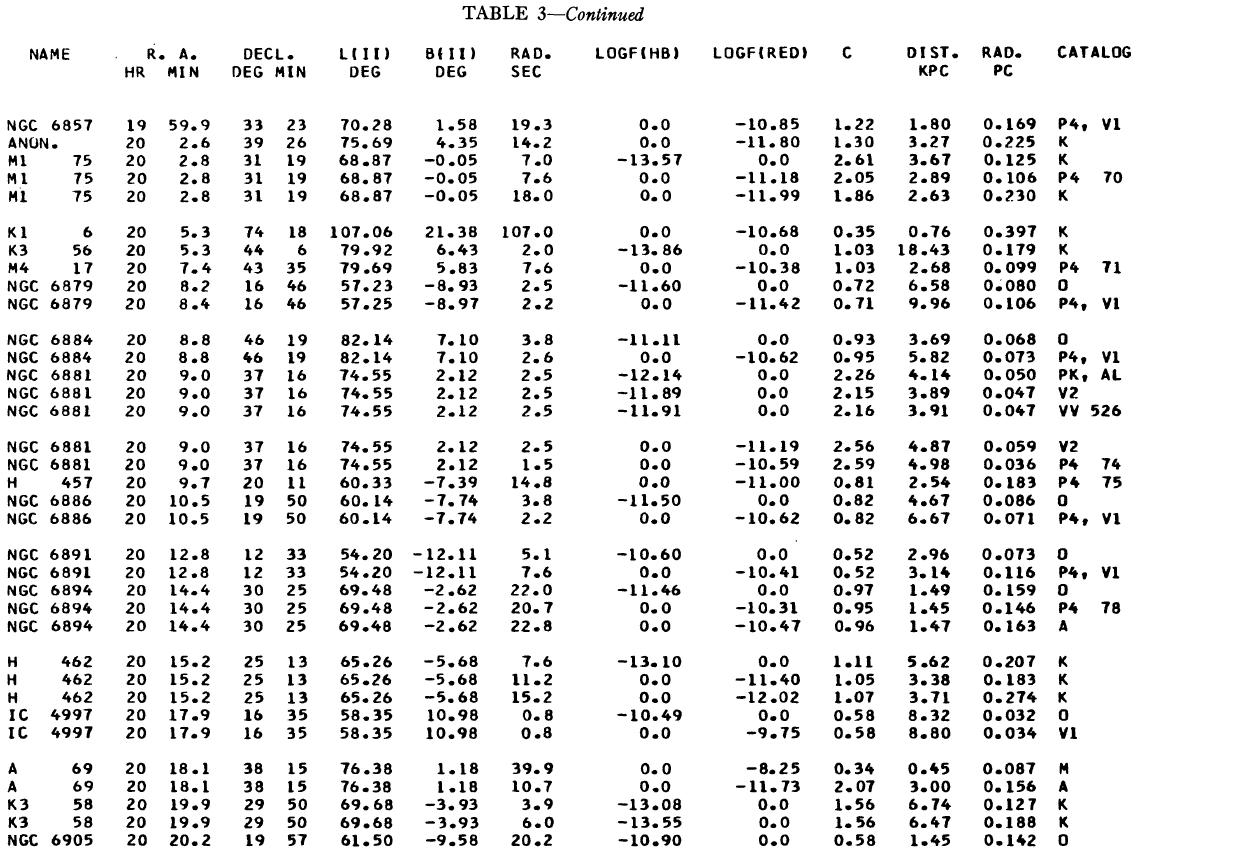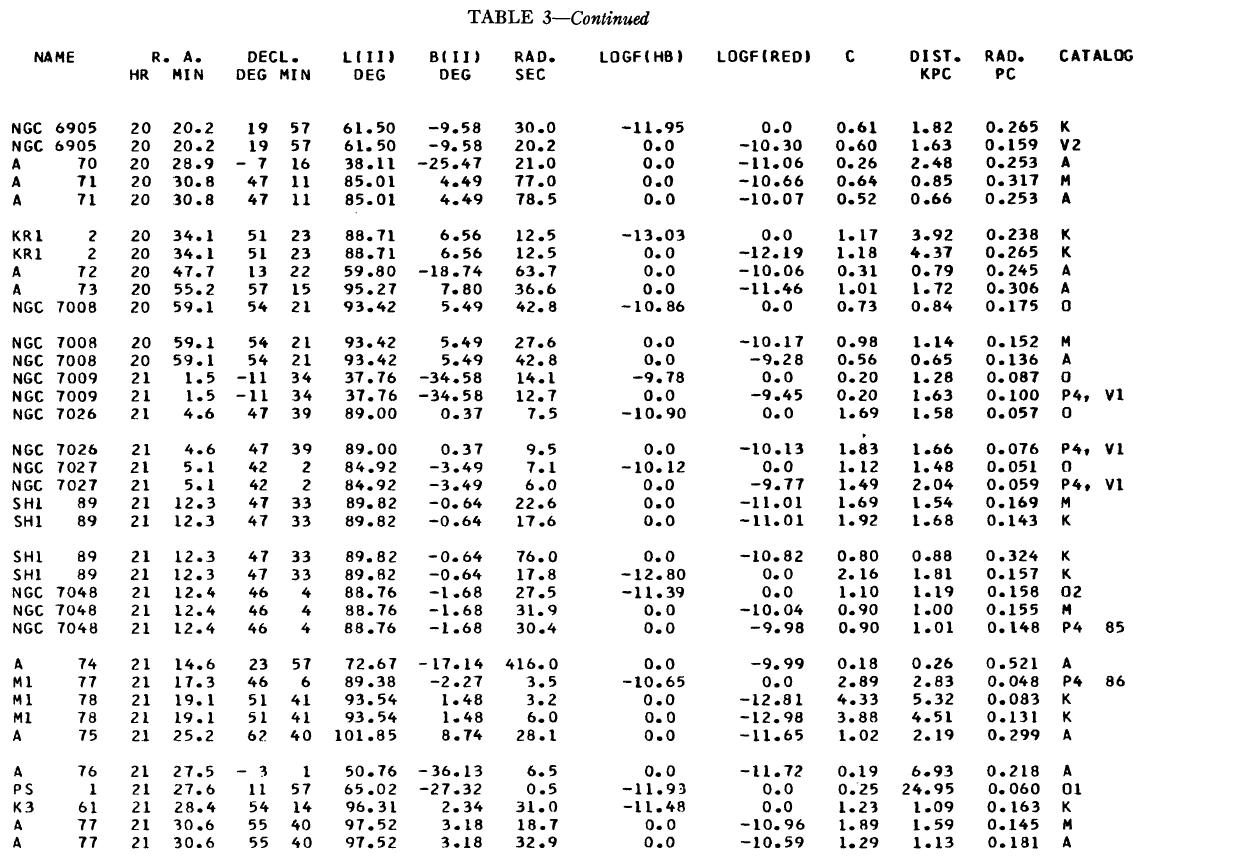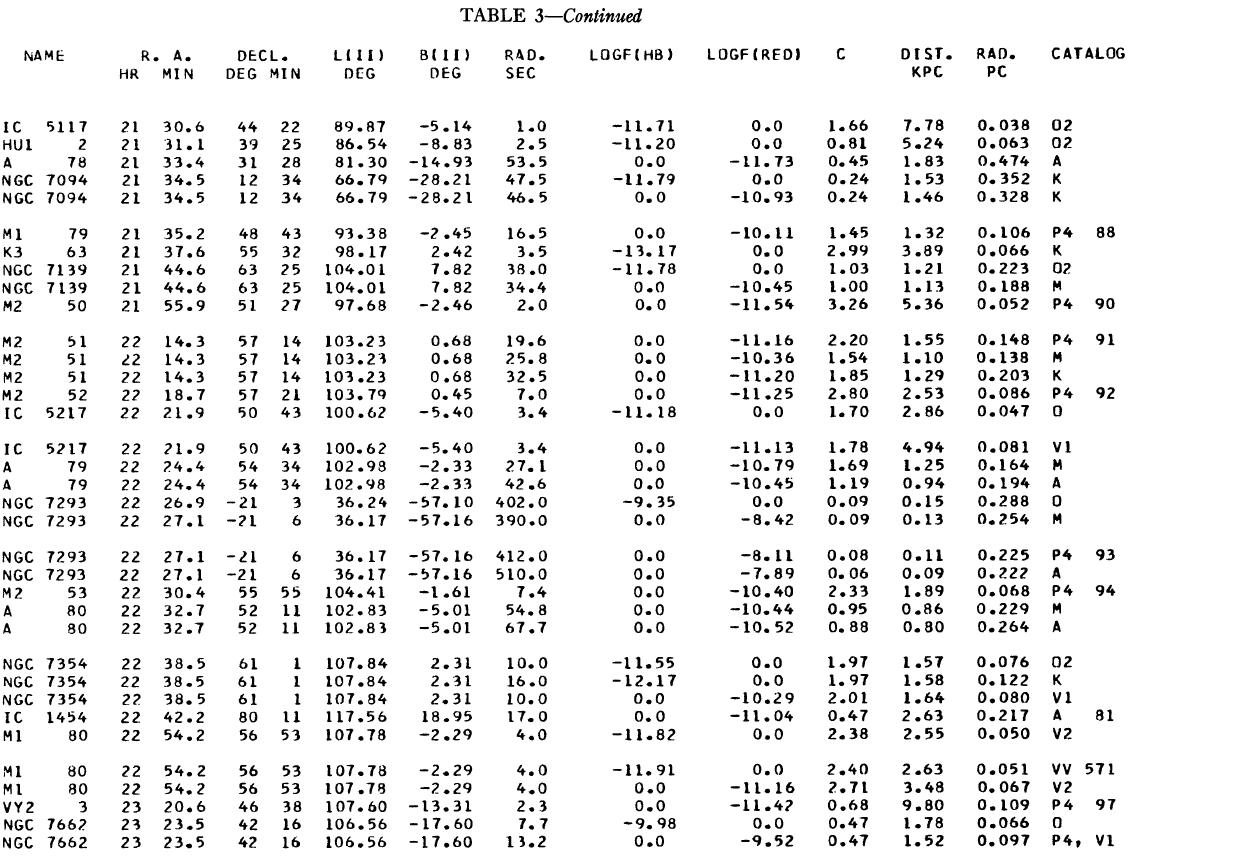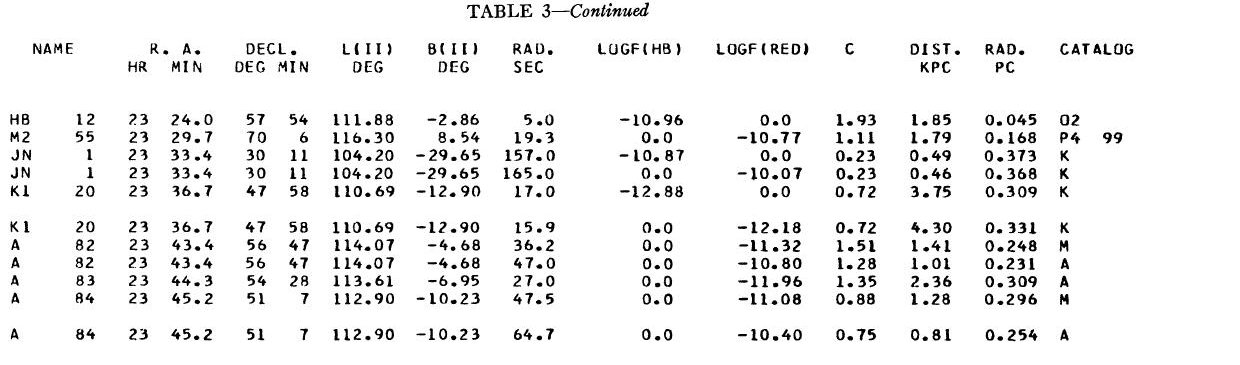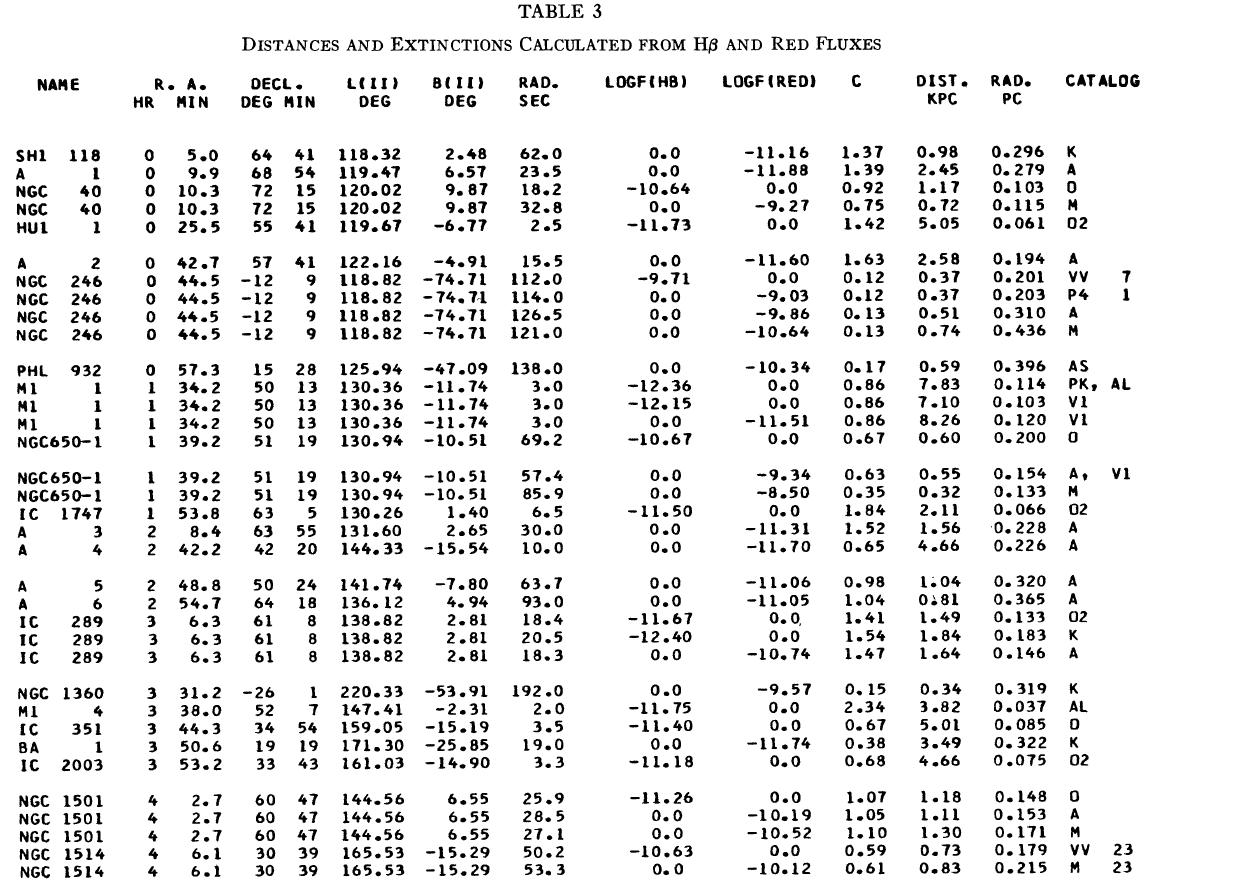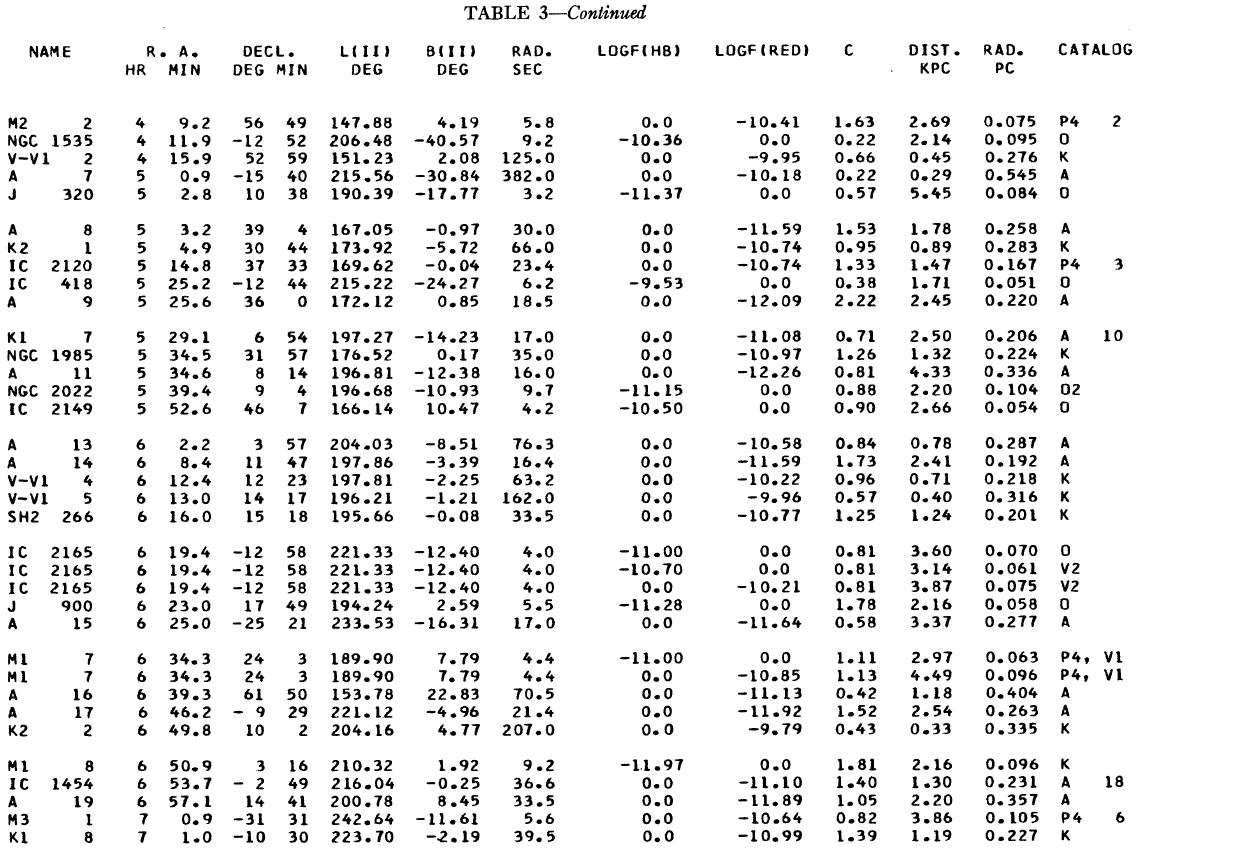 表１　観測減光の提示 　(4), (5)式を使っての c の決定は逐次近似的に行う。Hβ フラックスは表３ に載せた。表１には 10 cm 電波フラックス、c が載せてある。表１の第４列 ウエイトは電波, Hβ フラックスの精度を数字にしたもので２が信頼度高 である。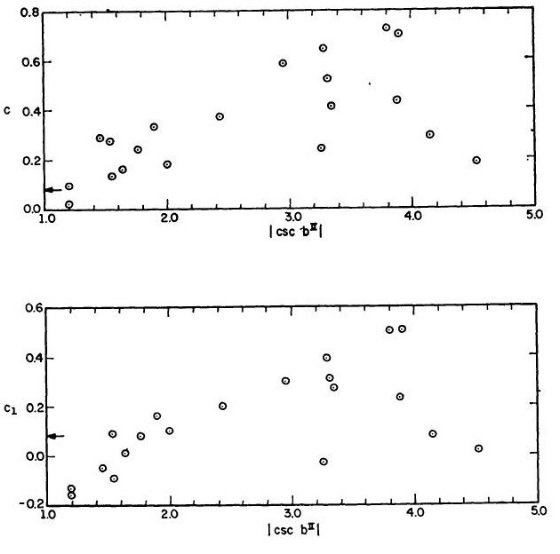 図１　星間吸収 c 対　|csc bII| 「電子温度」= 5000 K を 上の c 　　　の計算に用いた。一方、禁制線から導いた温度は下の c1 の計算 　　　に用いた。矢印は銀河観測から導いた銀極での減光量。

３．距離と計算減光の決定　

光学的に薄い半径の下限 R0 　Seaton によると、光学的に厚い星雲の半径をそれが薄いと仮定して得た値は 2R0 を越えない。したがって、表３で半径が 0.08 pc と 0.4 pc の 間にある星雲の距離と半径の信頼度は高い。 　 R0 の正当性に関しては図２が興味深い。光学的に厚い星雲では Δc が正になるはずだが、R = 0.04 pc で鋭い落ち込みがありそれ以下の データ点がない。また、R = 0.04 - 0.08 pc の間に Δc 大の星雲が集中している。 これらは、R0 = 0.04 pc と考えると自然に理解できる。 　光学的に厚い星雲の状況はやや複雑である。それらの天体は距離を過大に見積もり、 その結果減光も大きく評価している。しかし、距離が $sim; 10-0.2c と なるので、正しい減光が採用された時よりは影響が緩和される。 　図２に示した Δc の値は R0 < R < 2R0 の星雲が光学的 に薄いか、厚いかを決めるのに使える。もし、Δc ≈ 0 であるなら、 星雲は多分光学的に薄い。 　R0 に関して、表３を調べると、 R < R0 となっている のは、１３天体しかない。それらはフラックスの測定ミスである可能性が強い。 　図３には、半径 R > 2R0 の星雲について、表１からとった観測減光を 表３からの計算減光に対してプロットした。両者の一致は驚くほどである。 　似たような関係は図４にも見られる。ここでは、 R < 2R0 の星雲を 扱っている。従って、光学的に厚い星雲も混じっている。その場合、距離が遠くなり過 ぎる。そのために、図４の点は 45 ° 線の右側に分散している。 　系統誤差のチェックは図５で行われた。この図では Δc を銀経 l に対して プロットした。図の白丸は |b| < 10°, 四角は 10° < |b| < 40° の天体である。40° 以上になると Δc が小さすぎて意味を 成さない。図を見ると幾分か系統的な傾向があるようにも見えるが、判断できるほど データ点の数が多くない。 　NGC 6369 と NGC 2438 の２天体は他と離れているので注意が必要である。両者は 共に光学的に薄く見える。電波観測は 0.1.f.u.以下でエラーが大きい可能性が ある。 　ここに提示した星間吸収モデルは銀極で 0.25 mag の減光を与え、これは図１と 合致する。 モデルの問題点 　おそらく本論文で使用した距離決定法の最大の問題点は、全ての星雲が同一である と仮定した点にあろう。Kaler 1970 は He/H 比が星雲間で大きく異なることを示して いる。また、写真を見るだけでフィリングファクターが星雲毎に大きく変動すること も分かる。また、星雲質量が広い巾に渡っていることもかなり確かである。その上 電子温度の問題もある。 　式（８）のＫには、質量、He/H 比、フィリングファクター、電子温度が含まれて いることに注意せよ。個々の星雲質量を決めるのは最良の場合でも困難であるから、 他の観測可能なパラメターに観測値を入れるのは適切とは言えない。いずれにせよ、 それらの量は K の中に低次の指数で入っていて変動の影響は小さい。 図３．0.08 pc < R < 0.4 pc の光学的に薄い星雲に対する、観測減光と 　　　表３から計算された減光度との比較。

図２．Δc = 表３で計算された減光度と表１の観測減光度の差。 　　　横軸 R は |b| < 10° の星雲の表３半径。 図４　半径 R < 0.08 pc の星雲について、観測減光量と計算減光量の比較。 　　　光学的に厚い星雲が混ざってきて、点の分散は図３より悪い。 図５．Δc = 計算減光 - 観測減光 を銀経 l に対しプロットした。

電子温度 　「水素温度」の使用は直截にはＫに影響を及ぼさない。と言うのは、不定性が 他のパラメターの形ですでに吸収されているからである。電子温度を 5000 K から 12,000 K に上げると、式（７）から減光量を 0.19 下げる。これは Seaton(1968) の 式（６）によると、距離を 10% 下げる。この量はＫの不定性以下である。 他の方法で求めた距離との比較 　光学的に薄い星雲に対しては、本論文の方法でかなり良い距離の値が得られることは 表４を見ると分かる。そこには表１の距離と他の方法で得られた距離が比較してある。 表の２天体は分光的距離、４天体は画像の膨張率と視線速度の比（Liller, Welther, Liller 1966）から求めた距離、最後の４つは Lutz のＤ論から採った、観測減光量と 星の現行量ー距離プロットから出した距離である。 ２天体以外では一致は満足のいくものである。Seaton (1968) の K 法は大変よいこと が分かる。 　Perek, Kohoutek 1967 が出した距離を以前に求められた距離と較べると面白い ことが分かる。半径とフラックスに微かな周辺部まで含んだ星雲全体の値を使っても、 中心部の明るい部分のみを使っても計算される距離には無関係なようである。 　多くの場合、星雲までの距離は複数の方法で測られている。我々は距離を信頼度に 応じて並べた。電光測光された星雲は信頼度が高い。一般には様々な手法で決められた 距離の一致は良好である。

表３の距離と半径に関し、非常に重要な点は角半径が１秒以下の星雲が含まれている ことである。この値は通常は上限値であり、したがって距離、実半径は下限である。 しかし、問題はさらに複雑で、もし星雲が光学的に厚ければ距離は上限値ということに なる！したがってこの様な場合には数値の扱いには注意が必要である。

図６には光学的に薄い星雲の分布を銀河面上に投影した。また、図７にはＺ軸と 太陽ー銀河中心軸からなる面への投影を R๏ = 8 kpc を仮定して プロットした。 ４．ダスト距離　 これまで、惑星状星を同一の性質を持つ天体として距離を決めてきた。何度も指摘 してきた通り、ライマン連続光に対し光学的に厚いと距離を大きく見積もりすぎる。 図６ 銀河面上の光学的に薄い惑星状星雲の分布。太陽は(-8kpc, 0kpc) に位置する。

光学的に薄い星雲では、観測減光と計算減光との一致が良好であった。そこで、 やり方を反転して、（１）銀河系ダスト減光モデルと（２）観測減光とによって 光学的に厚い星雲までの距離を計算する。用いる式は（９）−（１３）である。この 方法は、|b| < 1-° で Δc が正の天体に限定する。高銀緯の星雲は 明らかにダスト層の外側にあり、距離と吸収は独立になるのでこの方法は使えない。 　この方法で求めた「ダスト距離」は表１の第（７）、（８）列に載せた。エラー はファクター２くらいあるが、それでも厚い星雲に対する距離の精度を大幅に上げた と言える。この方法は電波データが増加するとさらに有用になるであろう。 図７ X-Z 面への惑星状星雲の投影。太陽は（-8 kpc, 0 kpc)

５．惑星状星雲の分布　

この論文では出来るだけ多くの惑星状星雲の距離を求めることを主眼とした。選択 効果があるので、統計的扱いは困難である。厳密な処理は後の論文に書く。ここ ではラフな結果を述べる。中心的な問題は光学的に薄い星雲、つまり 0.08 pc < R < 0.4 pc の局所密度である。R0 < R < 2R0 の 天体は捨てた。すると、 １．半径分布 　太陽からの距離に対しその距離内の星雲数を 1 kpc 以内でプロットすると、 図８のようになる。半径 R = 0.08 - 0.4 pc の星雲は光学的に薄いと仮定し、 さらに等速膨張に対して期待される各半径枠内で均等な分布は、選択効果により 阻害されていると考える。 　図８の横軸は R =R/0.08pc である。図の点線は Seaton 1966 の主張、 　　　　　　　　　N( R ) = N(5)　　　　　　　　　　　　　1 ≤ R ≤ 5 　　　　　　　　　N( R ) = N(5)(5/ R )19/6　　　　　　 R > 5 R = 5 は　R1 に対応する。 　ここで強調したいのは、もし R > R1 の星雲が光学的に薄くても、 それらを統計的な処理には用いるわけにはいかない。なぜなら、表面輝度が下がると 検出率が下がってそれが実際に図８の R > R1 で起きていることだから である。選択効果を補正すると、太陽から 1 kpc 以内の惑星状星雲の数は 52 である。 すると、局所密度は、 　　　　　　　　　DL = 52/(4π/3) = 12.4 kpc-3 　半径 0.5 kpc の星雲数２４からは局所密度 = 46 kpc-3 が得られる。 星雲が太陽の周りを球対称には分布していないことを考えると、後の値の方が正当 である。厚み 0.5 kpc × 2 = 1 kpc でも厚すぎる。 図８　太陽から 1 kpc 以内の惑星状星雲の半径分布。点線は R > 0.08 pc 　　　の星雲が R > 0.4 pc で光学的に厚いという仮定でのモデル分布。

２．Ｚ方向分布 　太陽から半径 1 kpc の円柱内で光学的に薄い星雲のＺ分布を以下のように定めた。 dN = 196 exp ( - Z ) dZ 0.09 これは局所密度 　DL = 196/&pi = 62.4 kpc-3 に対応する。 ３．Allen 1954 の解析 　Allen は明るい２０天体を解析した。図９には　log N 対 mn がプロット されている。図には明らかな折れ曲がりが見られる。Allen は平均絶対等級 Mo を 仮定して得た局所密度 Do と、単位体積当たりの可視放射光を最大にする絶対光度 M1 から導いた密度 D1 を出した。Do = 300 kpc-3, D1 = 58 kpc-3 であった。 D1 は我々が出した 値に近い。 図９　mn　より明るい惑星状星雲の数（総数＝２０）

４．銀河系全体での分布 　Perek 1962 は銀河系分布関数として次の形を考えた。 　　　　　　　　　D = DC exp( - m )　　　　　　　　　(14) ここに、　　　　　m2 = (ω/aD)2 + (Z/cD)2　　　　　(15) で、(12), (13) 式と同じ m である。 DC は銀河中心での密度である。 銀河系全体での惑星状星雲総数 三つのパラメター、 DC、aD、cD をフィットする ため、太陽を中心にＺ方向を軸とする立体角 Ω の円帽上で（１４）式を積分する。 dN = r2 DC ∫ exp ( - m ) dΩ dr Ω 　R๏ = 8 kpc と 10 kpc の二つに対して、（１４）式をフィット した結果を表５に示す。銀河系内の惑星状星雲総数は、Perek 1962 により、 　　　　　　　　　N = 8 π aD2 cD DC で与えられ、表５に載せてある。 惑星状星雲の誕生率と死亡率 　惑星状星雲の誕生率と死亡率を知るには、その局所密度 DL が必要である。 今までの値は皆似たり寄ったりなので、 DL = 50 kpc-3 とする。 この値を半径 0.08 - 0.4 pc の間で均等に分配すると、単位半径当たり数密度として、 　　　　　　　　　N(R) = 50 / 3.2 × 10-4 = 1.6 × 105 kpc-4

膨張速度 V = 20 km/s = 2 × 10-8 kpc/yr を仮定すると誕生率は、 　　　　　　　　　&ki;PN = V N(R) = 3.2 × 10-3 kpc-3 yr-1 　Weidemann 1968 によると、白色矮星の誕生率は、 　　　　　　　　　&ki;WD = (1.6 - 5) × 10-3 kpc-3 yr-1 で、大部分の白色矮星が惑星状星雲の段階を経て誕生するという見方と合致する。 　最後に、銀河全体での惑星状星雲の誕生率を求めると、 　　　　　dN/dt = 8 π a2 c &ki;C = 8 π a2 (cD/aD) &ki;PN exp (10/1.4) = 42 /yr ここに、 &ki;C は銀河系中心での誕生率である。

　表１　９５天体の観測減光と補正距離　

　表３　Hβ と赤波長　フラックスからの計算減光と距離