Properties of Two Intergalactic Globular Clusters

　アブストラクト　

　０．イントロダクション　

　１．11h 星団　

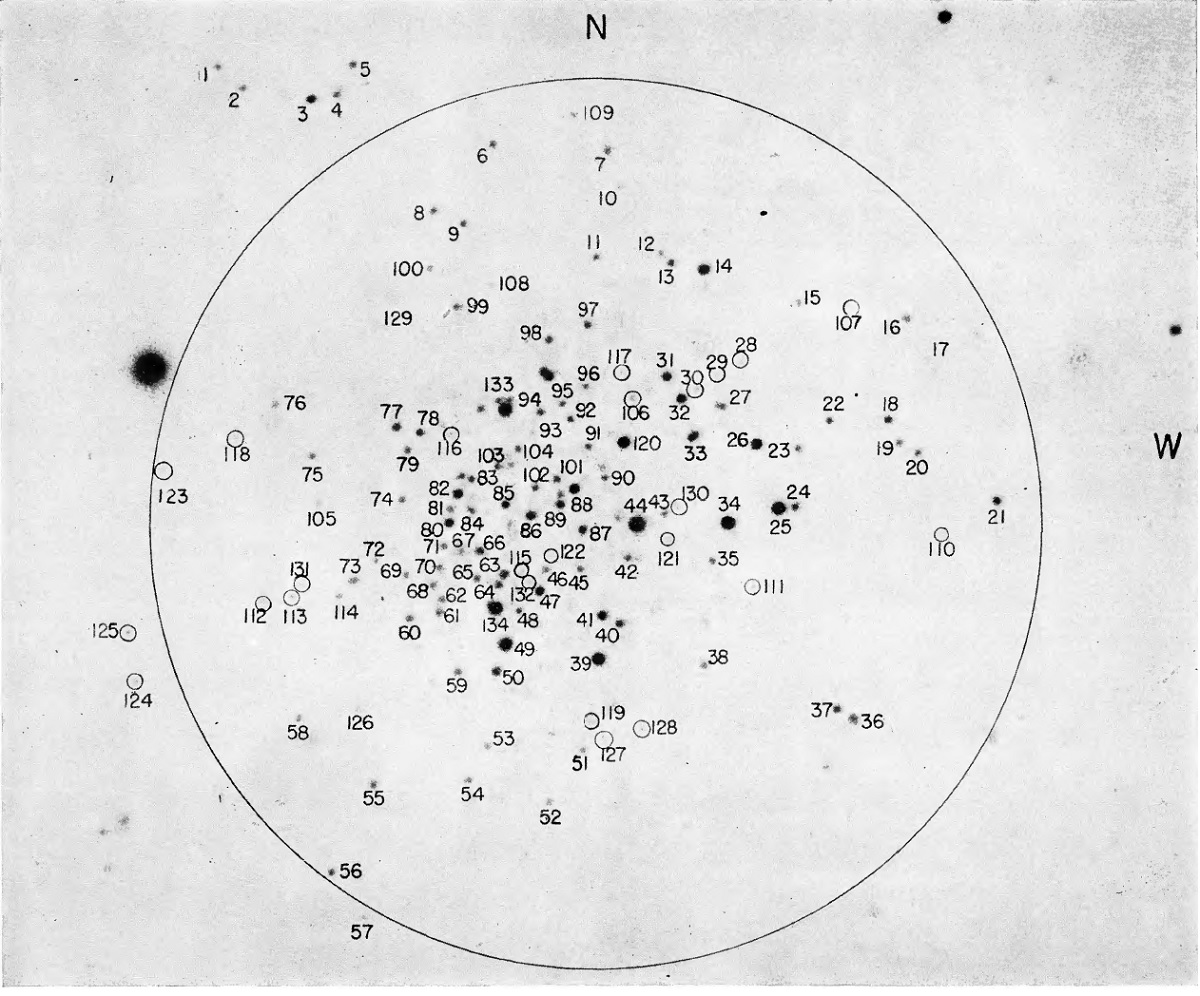
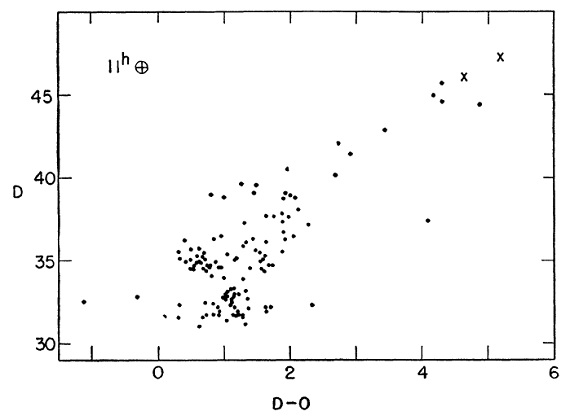図２．１１h 星団の擬 CMD＝ 103a-D 乾板の測光器の読み D を 103a-D と 103 a-O の読みの差に対してプロット。 バツ印＝変光星 24 と 44. 　１．１．CMD と距離　 　大きな視直径と低い中心集中度　 　図１ は２００インチ　103a-D 乾板 + GG11フィルターでの 11h 星団＝ Abell No.4 の限界撮像である。 はっきり視別できる内で最も暗い星は V = 22 mag である。星団中最も明るい 星は V = 17.5 である。星団の直径は 150 arcsec に達する。中心集中度の低 さから、この星団は NGC 5053 や NGC 5897 と同じグループに属すると思われ る。集中度クラス＝ XI か XII である。 (図１は変 ) 　図２＝擬 CMD　 　きちんとした測光はまだ完成していない。その前に、iris 測光器の較正曲線 が等級に対してかなり線形性がよいことを利用して、仮の CMD をこしらえた。 図２にそれを示す。通常の球状星団 CMD との類似性は明らかである。測光の際に 見つかった二つの変光星はバツ印で示した。

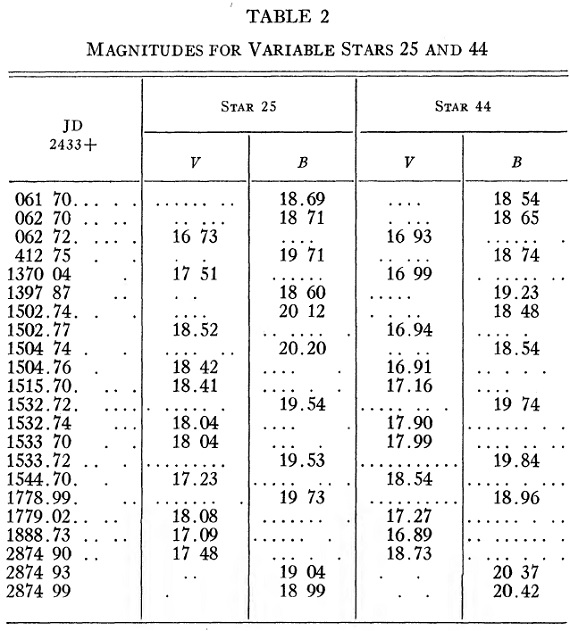表２．変光星 25 と 44 の等級変化。 　B, V 測光　 　表１には 11h 星団の測光結果を、図３にはそのファインディングチャートを示す。 星団には RR Lyr 星はない。表２には変光星 25 と 44 の等級変化を示す。

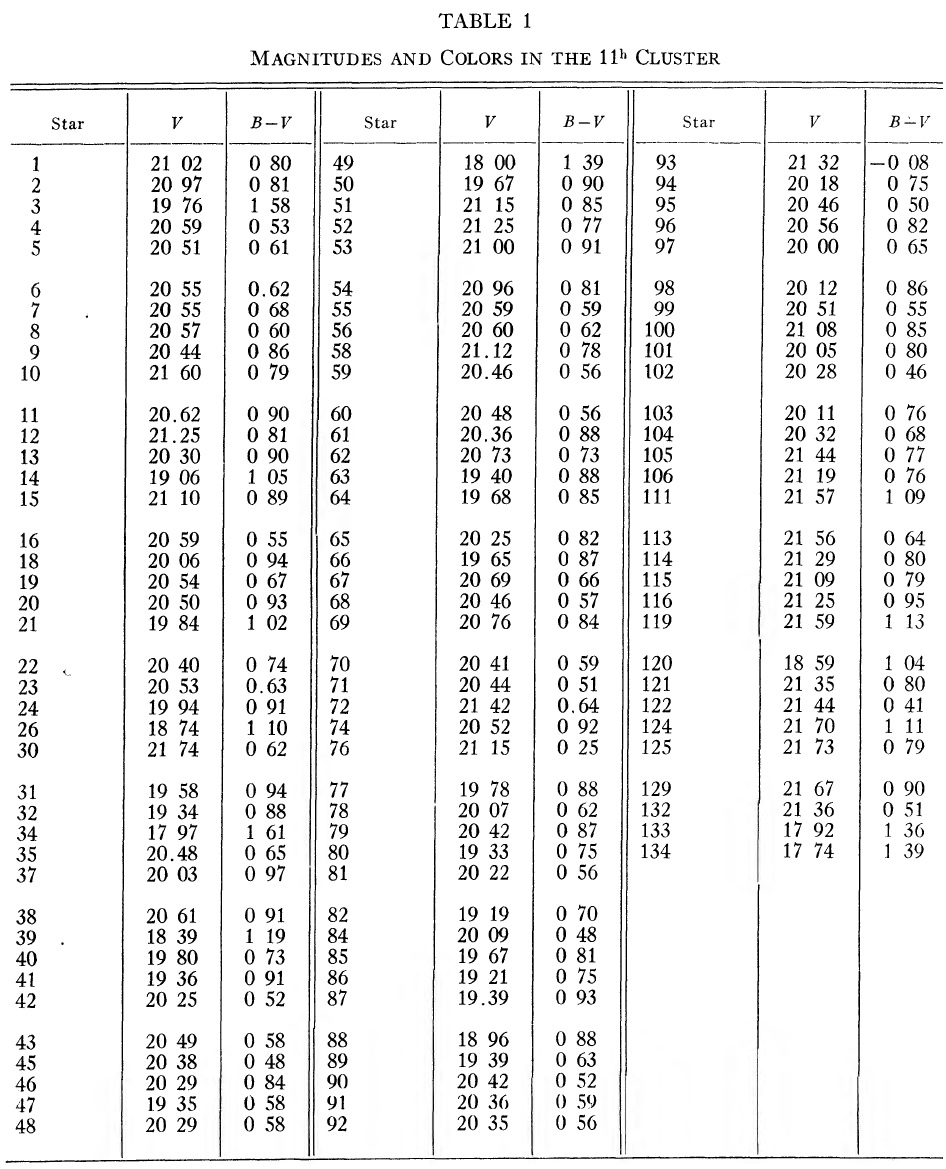
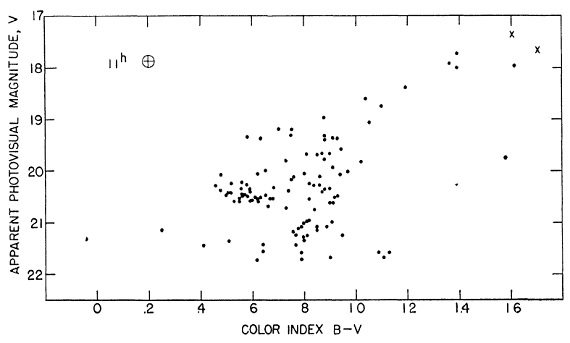図４．１１h 星団の CMD. 表１の B, V 等級をプロットした。 　図４＝ CMD　 　図４には表１の B,V 等級からの CMD を示す。 （１）巨星枝の先端は B-V = 1.6 である。 （２）巨星枝勾配は B-V で水平枝を分岐する。それより下の sub-giant branch はほぼ垂直である。 （３）水平枝と巨星枝先端との等級差 ΔV = 3.0. （４）B-V < 0.4 の水平枝星がない。 （１）−（３）は普通だが、（４）の球状星団は他にない。通常の球状星団は M13, M10, M2, M92, M15, M5, M3 の系列に並ぶ。M13 側は極度に青い RR Lyr に富み、M3 側では青と赤の数比はほぼ等しい。この順序は、巨星枝が次第に 赤くなり、また RR Lyr 星周期が短くなるという系列に反映されていた。 　11h 星団 CMD の特徴　 　水平枝星分布の点では 11h 星団は球状星団系列上 M3 を越えてさらに右に 位置する。しかし、水平枝上分布と RR Lyr 平均周期との相関からは警告が発 せられる。Sandage 1958 による、二つの星団間で水平枝平均等級の差 ΔMv と RR Lyr平均周期の差 ΔlogP の関係を用いると、M3 グループと M92 グループの間では ΔMv = 0.2 mag が予想される。M3 グループの変光星 は暗いと考えられる。すると、11h 星団では Mv = [0.2, 0.5] と考えられる。 　Mv = 0.00 を仮定し、観測値 V = 20.5 を加えると、減光を無視して m-M = 20.5, D=125 kpc を得る。これは M31 の m-M = 24.6 の距離の 1/5 である。 もし、水平枝光度が Mv = 0.5 なら、m-M=20.0 D=100 kpc となる。 　１．２．光度関数　 　星団の性質　 　表３には等級別の星数を示す。φ(Mv) は半径 95 arcsec 内の [Mv-0.1, mv+0.1] 区間内の星の数である。星団 11h の半径 95 arcsec 内にあり、 Mv < 1.1 の星は 123 個である。図５には φ(Mv) ヒストグラムを示す。 図５には M3 の光度関数を規格化してしめす。M3 と同じ光度関数を仮定すると 11h 星団の積分絶対等級は m-M=20.5 の場合、Mv = -6.35 となる。１１ｈは 球状星団の中では最も暗いグループに属する。また、 M/L = 1 を仮定すると、 M = 1.8 104 Mo, 星総数は = 4.3 104 である。 van den Bergh の乱暴な研究　　 　 van den Bergh (1956)はパロマースカイサーベイの写真から M67, M3 の既 知星を選んで像径を測り、較正曲線を作成した。彼はそれを用いて 11h 星団の 等級測定を行った。これは、 M67, M3, 11h 星団乾板の露出、現像、時期が同 じでないことを考えると、乱暴な方法である。にも拘らず、彼の得た値は上と そこそこ近い。その上、彼はこの星団の特異な性質に注意を促した最初の研究者 である。

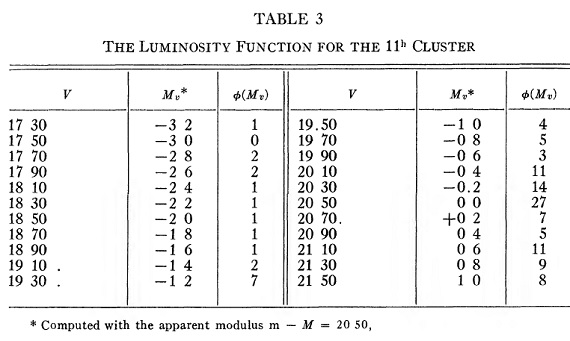表３．１１h 星団の光度関数。 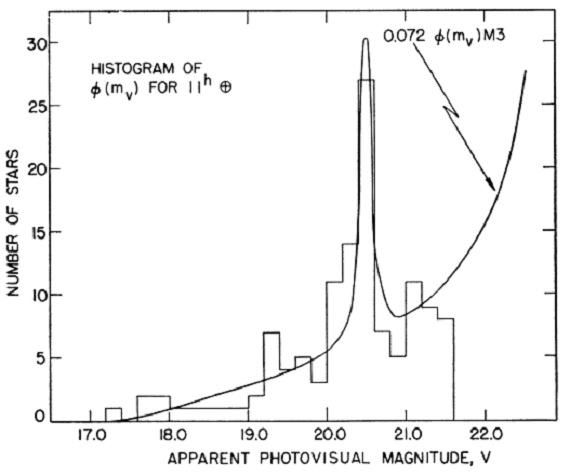図５．１１h 星団の光度関数。実線＝ M3 光度関数を 0.072 倍した。 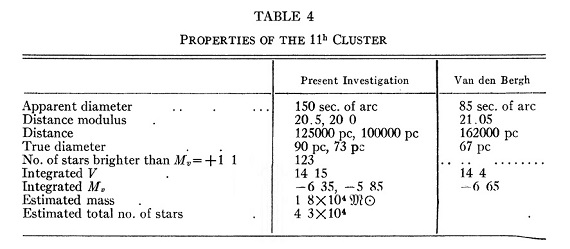表４．１１h 星団の性質。

　２．10h 星団　

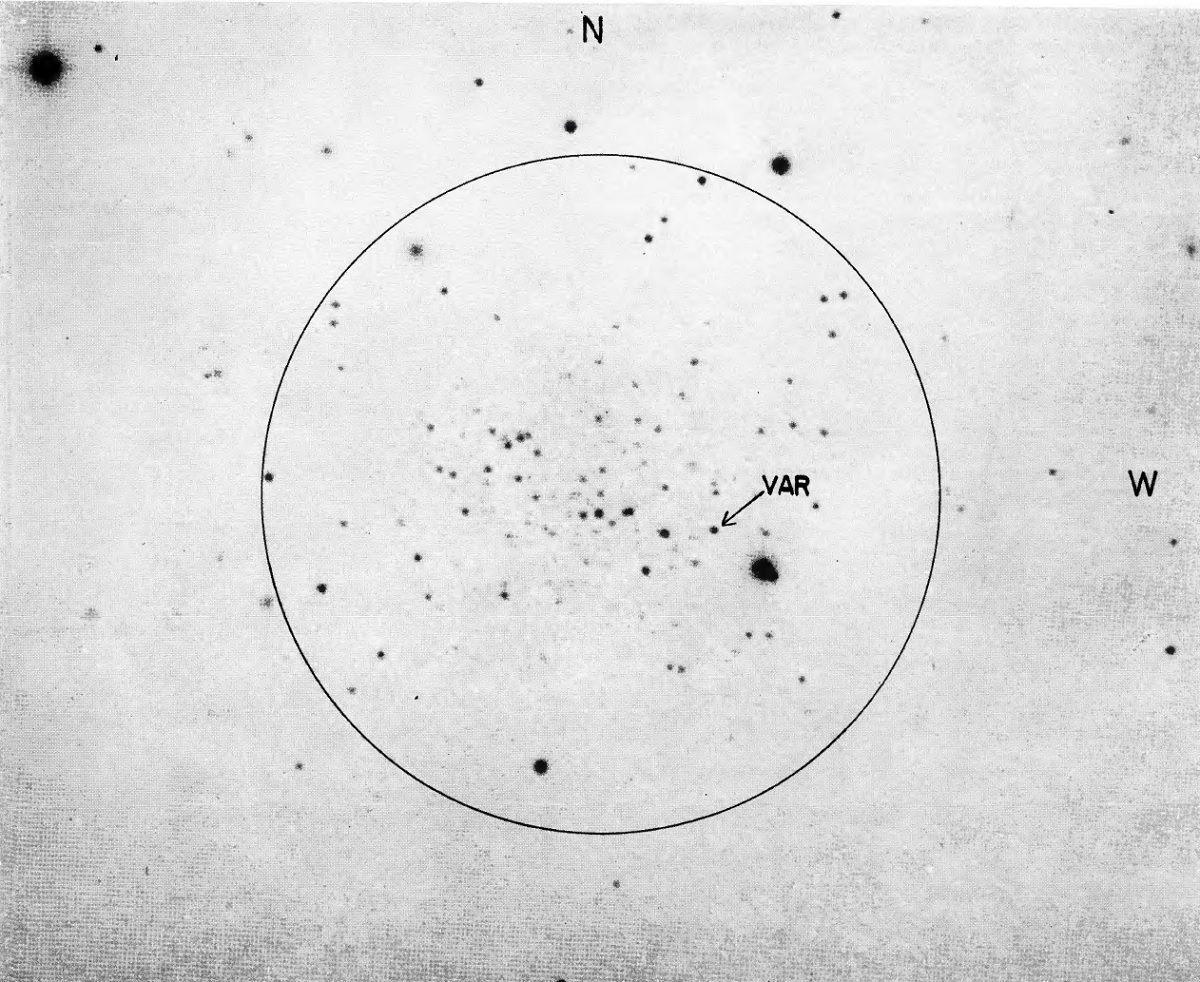
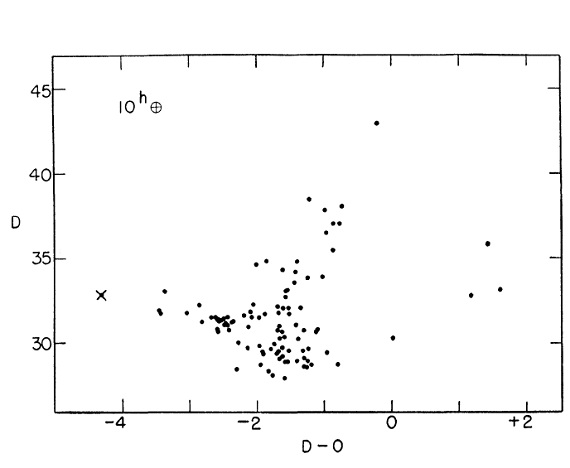図７．10h 星団の 200 インチ写真。103a-O + ショット WG2. 円は直径 168 arcsec. 　星団画像　 　10h 星団＝Abell No.3 はRA(1950)=10h03.0m, Dec(1950) = +00°18' にある。測光基準が SA 57 だけなので、この天体のデータは 11h 星団ほど 正確でない。図６はパローマー２００インチで撮った 103a-D+GG11 画像であ る。図７には擬CMDを示す。予備的な較正は表５に示す。 　10h 星団擬CMDの特徴　 （１）巨星枝の先端が V=17.8, B-V=1.6 にある。 （２）準巨星と水平枝の分岐が V=20.6, B-V=0.9 で起きる。 （３）水平枝の平均等級は V = 20.6. 巨星枝先端と水平枝との等級差は従って、ΔV = 2.8 mag である。これら の数値は 10h 星団が典型的な球状星団 CMD を有することを示す。この星団は 11h 星団より正常で、水平枝は青い方へ伸びている。銀河系減光を無視すると m-M = 20.6 となる。 　変光星　 　変光星は一つだけ見つかっている。それは図６に同定され、図７ではバツ印 で示した。これはほぼ確実に RR Lyr 星であるが周期と変光曲線は測られていない。 　星団光度　 　Mv = 1.1, V=21.7 より明るい星の数は図７の円内に 76 星である。この範囲 内に 11h 星団と同じ光度関数 φ(Mv) を仮定すると、星団積分等級として Mv = -5.9 を得る。CI = 0.50 を仮定すると Mpg = -5.42 となり、10h 星団 は最も暗い星団グループに属する。表６にまとめを示す。

表５．図７の予備的較正。 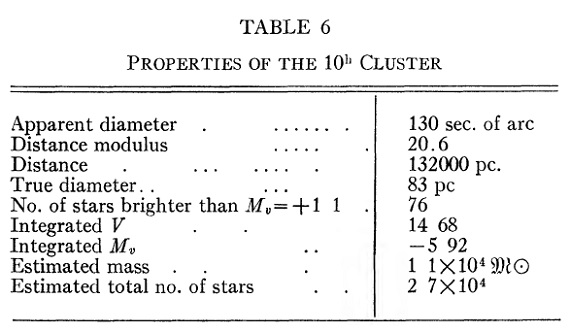表６．10h 星団の性質。

　３．議論