|
外側銀河系の速度場を l = [90, 270], R = 17 kpc = 2 Ro まで与える。
速度場は内側銀河系に対しても太陽から 2 - 3 kpc まで与える。データセット
は HIIR と反射星雲のサンプルである。それまでの距離は測光で定める。また
付随する分子雲の視線速度も利用する。それらに HI 接点データを加えた。
データ点は R = [0.2, 2] Ro に亘る。Θ = 回転速度とし、 Θ/Θo = a1(R/Ro)a2 + a3 で近似すると、Ro = 8.5 kpc, Θo = 220 km/s とした時、 a1 = 1.00767, a2 = 0.0394, a3 = 0.00712 となる。回転曲線はほぼ平坦で あるが、最外側点は僅かに上がる傾向を示す。 R = 2Ro までの銀河系質量は 4.1 1011 Mo である。 | 残差視線速度=Vlsr(観測)-Vlsr(モデル) のパターンは純回転からのズレを 示唆する。そのズレは渦状密度波の流れに合致する。我々のサンプル中の 早期型星の分布に渦状構造の証拠は見られなかった。ストリーミング=残差 速度に見られる系統速度成分が見つかった。その平均速度は 12 km/s で、 2D速度としては 17 km/s である。LRS では分子ガスが l = 180° から l = 0° 方向に 3.8 km/s で流れていることを見出した。回転曲線の南側と 北側の差は小さく、20 kpc で 5 % である。 太陽から [0.7, 2] kpc にある局所分子雲サンプルから、太陽は銀河面の 13 pc 上にある。分子雲スケール高は 65 pc である。 |
|
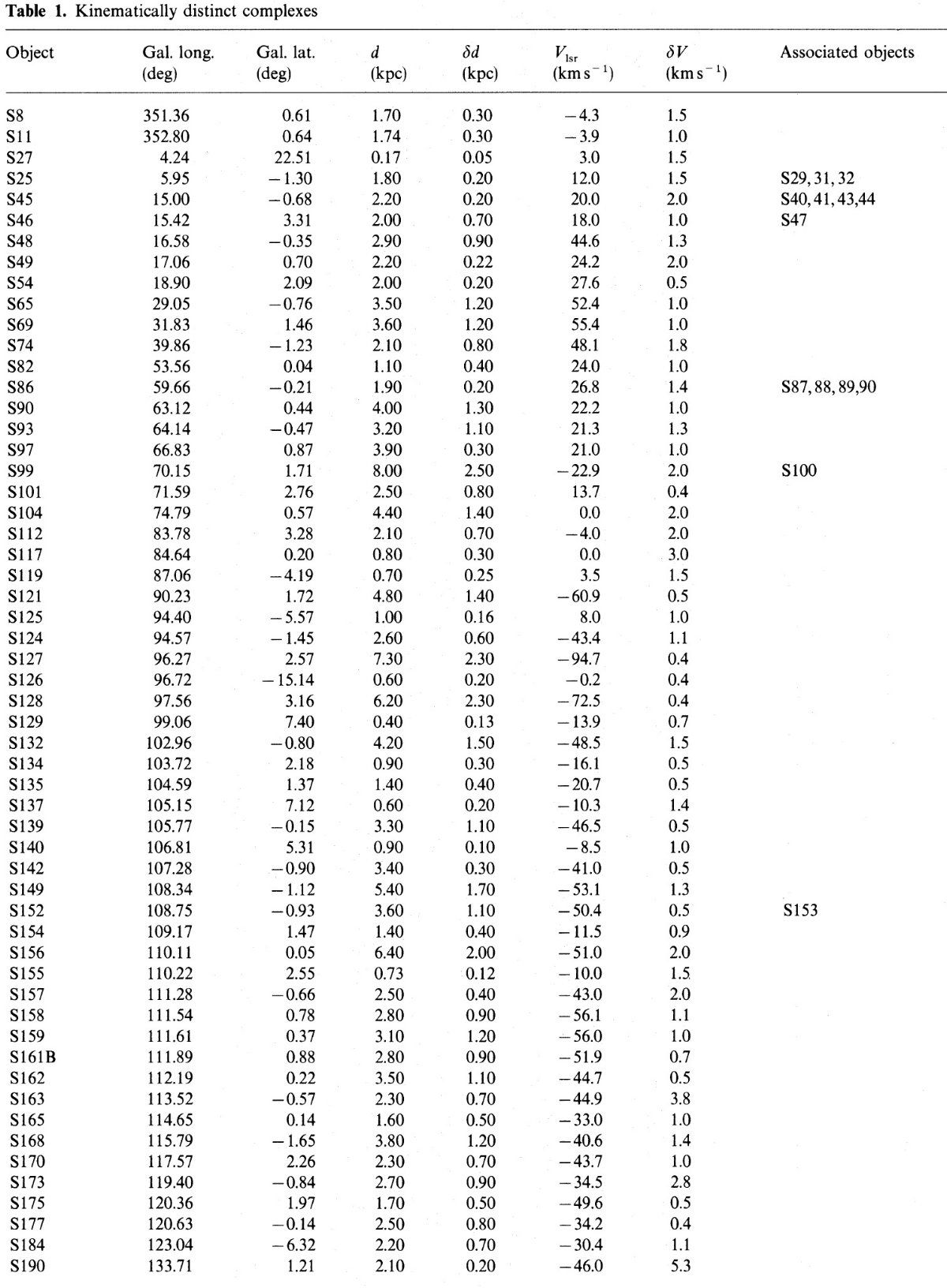
l = [230, 305] 400 可視 HIIR (Brand et al 1986) l = [351, 360], [0, 243] 銀河星雲 (Blitz et al 1982) l = [305, 350] に適当なカタログがない。 HI データ使用。 | サンプル中の星雲は位置と速度が近いグループに分けた。表1にそれらの グループの性質を載せる。 |

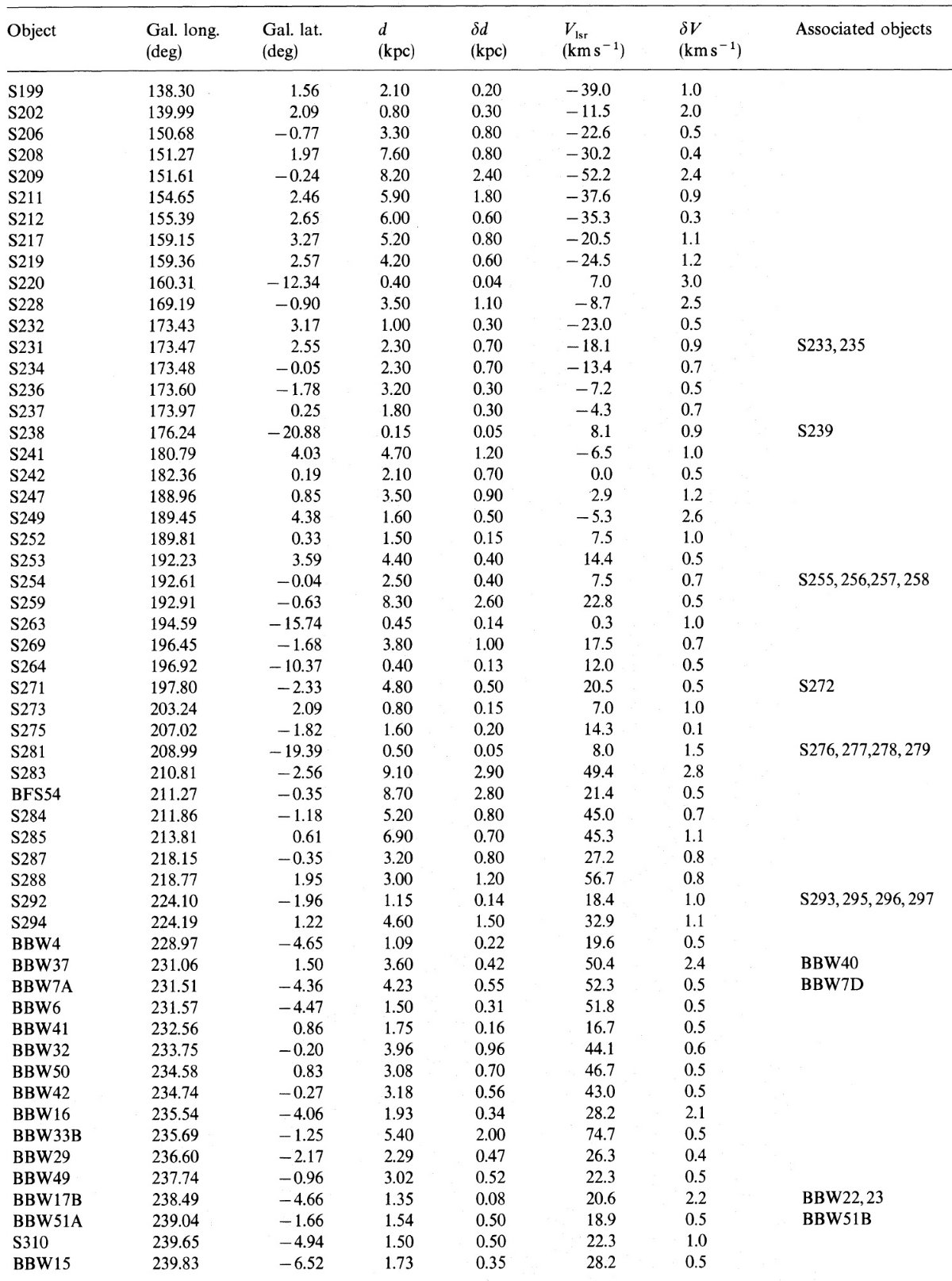
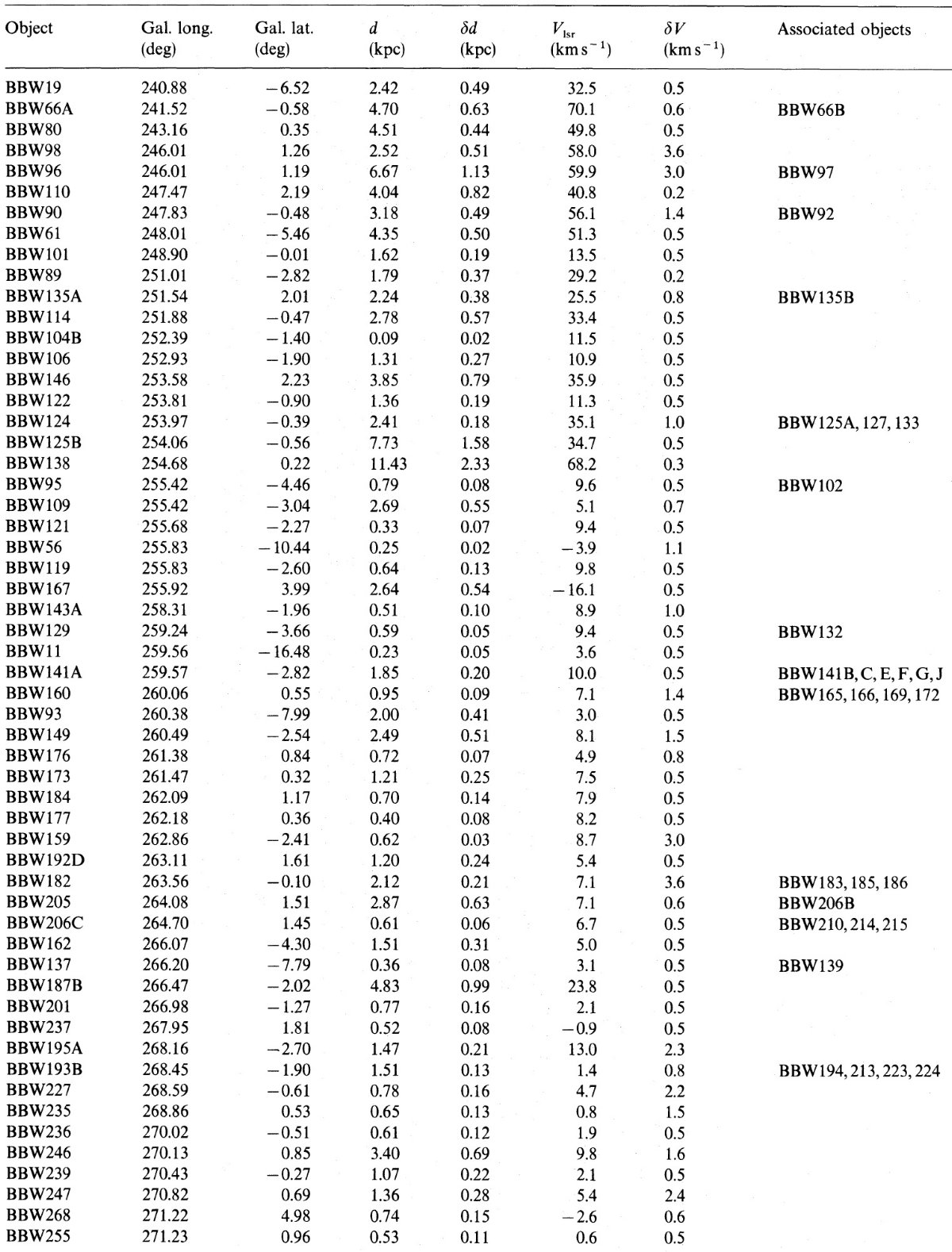
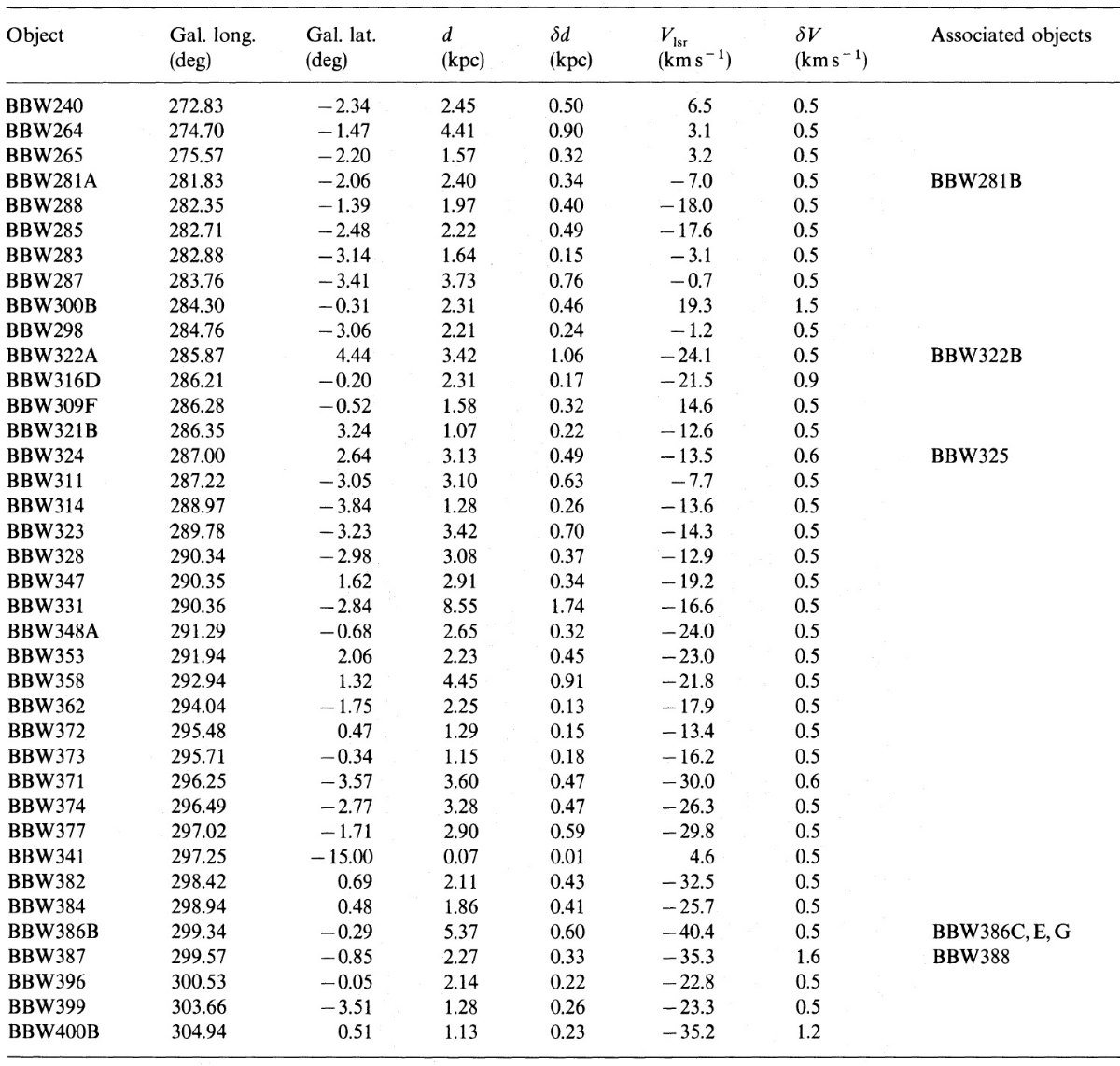
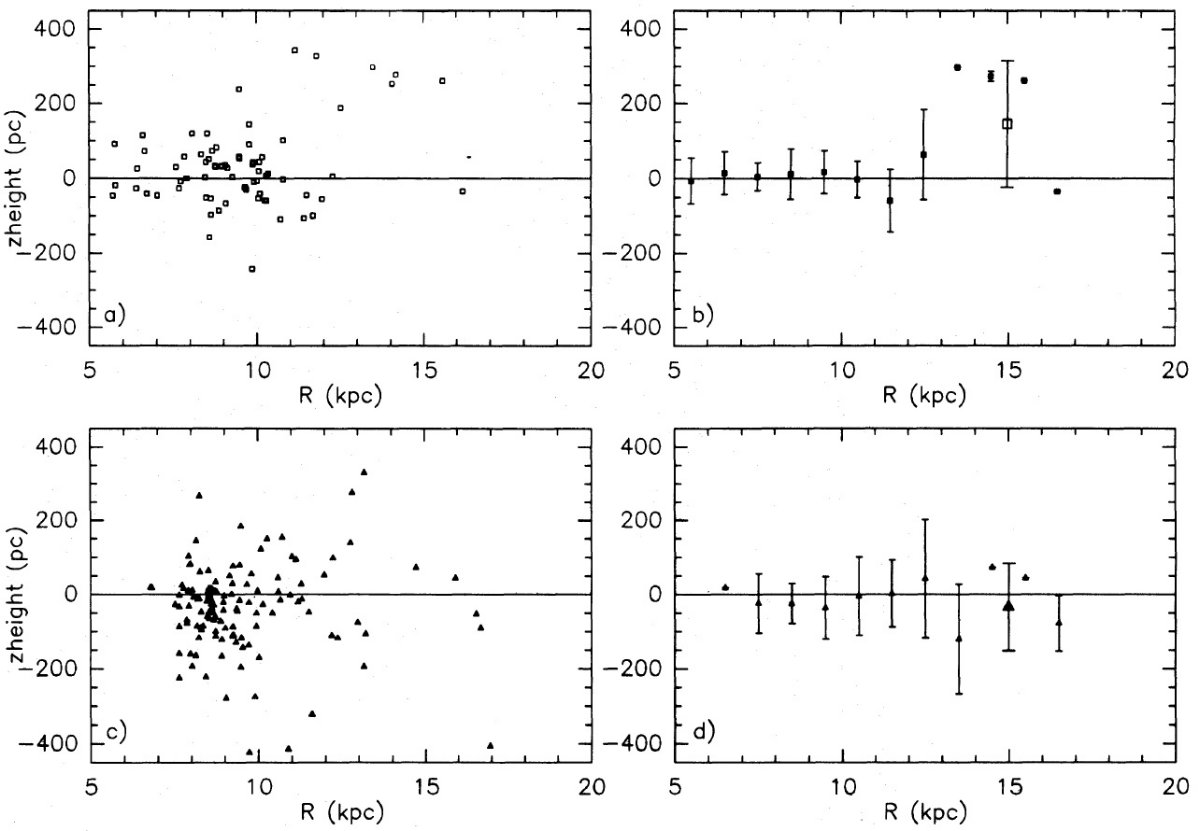
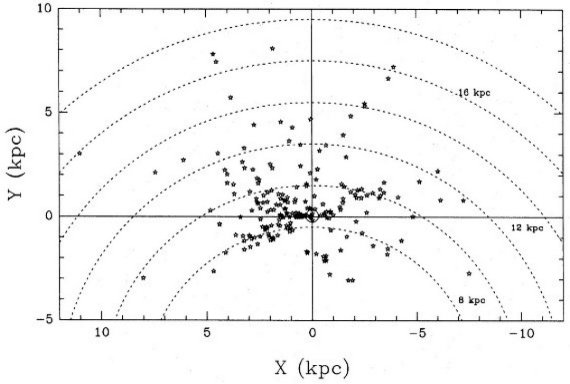 図1.表1にある天体の位置分布。太陽は (0, 0) で銀河中心は (0, -8.5). 点線= R 一定ライン。 |
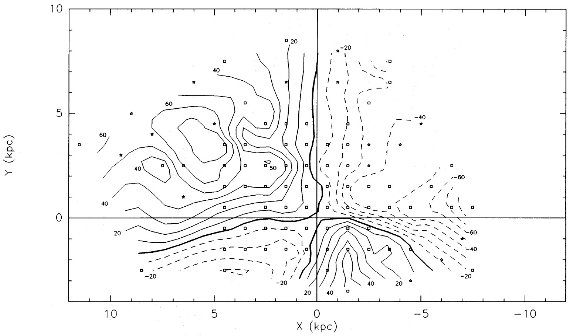 図2a.銀河面上のサンプル天体の視線速度分布。等高線は 10 km/s 間隔。 速度場を平滑化するため、視線速度データは 1 kpc2 区域で 平均化した。データ点が欠けるか、粗い個所では内挿値を用いた。この速度場 には非円運動成分も含まれている。 |
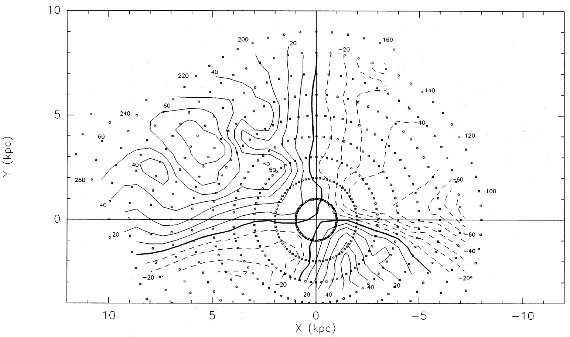 図2b.図2a と同じだが、正方グリッド点のかわりに、Δl = 5°, ΔD = 1 kpc グリッドを付けた。この方が使いやすい。 |
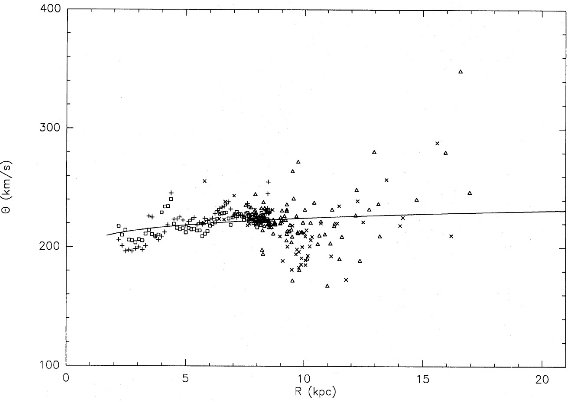 図3.円運動速度 Θ と R の関係。太陽は (Ro,Θo) = (8.5, 220). プラス=北 HI. 四角=南 HI. バツ=北 HII/CO. 三角=南 HII/CO. 実線=フィット回転曲線。 |
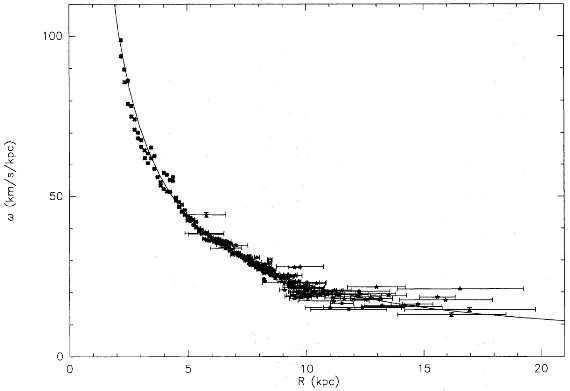 図4a.図3から決めた ω = 角回転速度と R の関係。 |
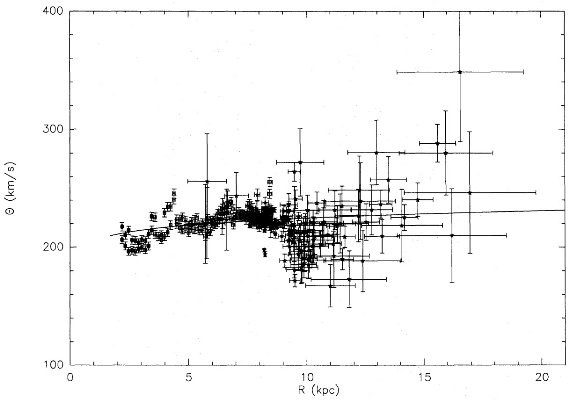 図4b.図3と同じだが、エラーバーを足した。 |
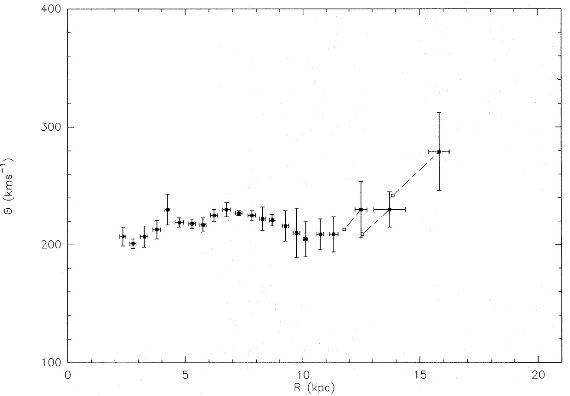 図5.図4b と似るがデータを R でまとめ、平均値を使う。白記号= 元素勾配の影響を示す。 |
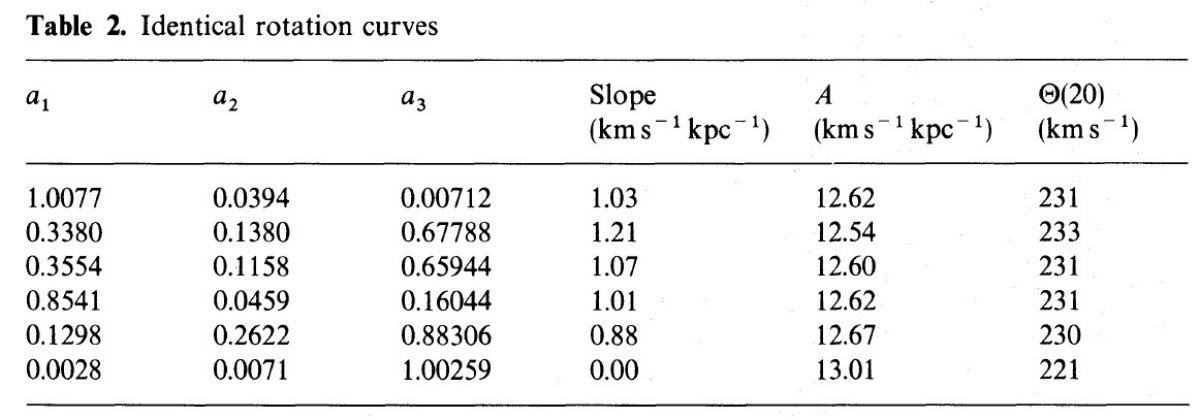
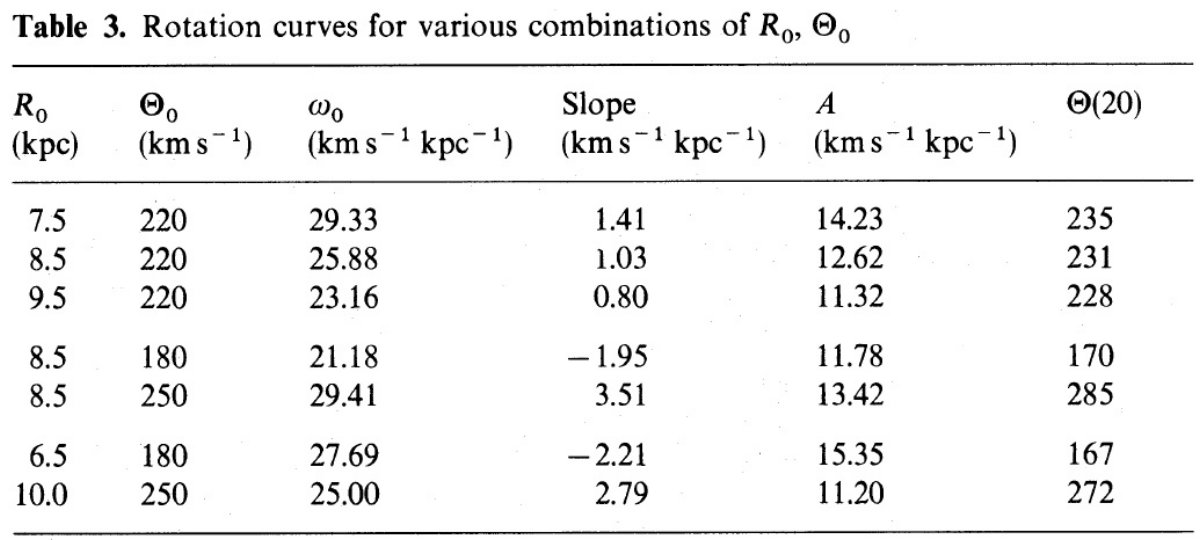
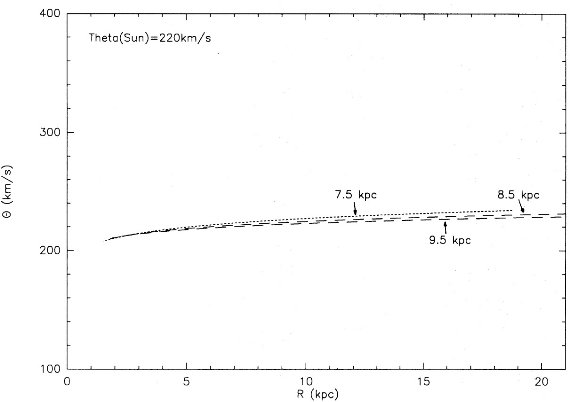 図6a.Θ = 220 km/s で Ro = 7.5, 8.5, 9.5 kpc とした時の回転曲線。 |
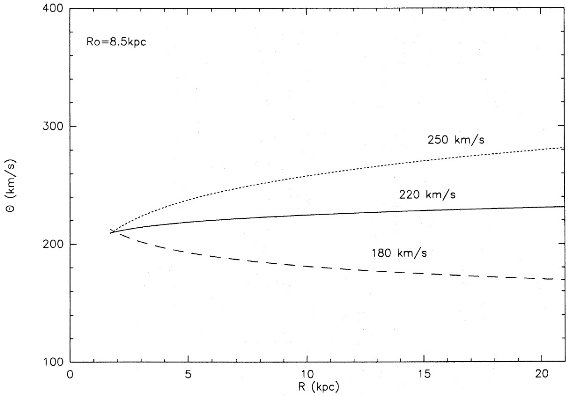 図6b.Ro = 8.5 kpc に固定.Θ = 180, 220, 250 km/s の回転曲線。 |
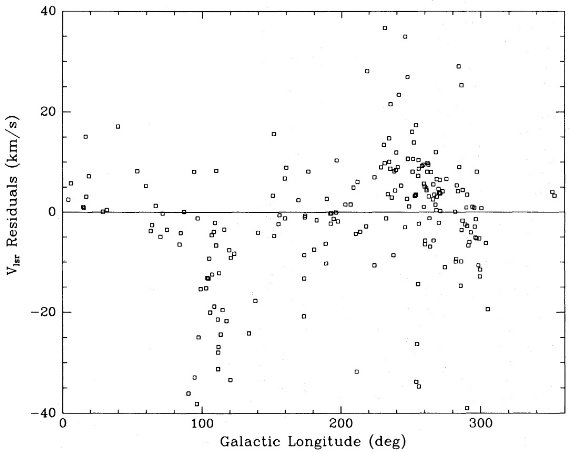 図7.残差速度=Vlsr(観測) - Vlsr(モデル) と l の関係。 |
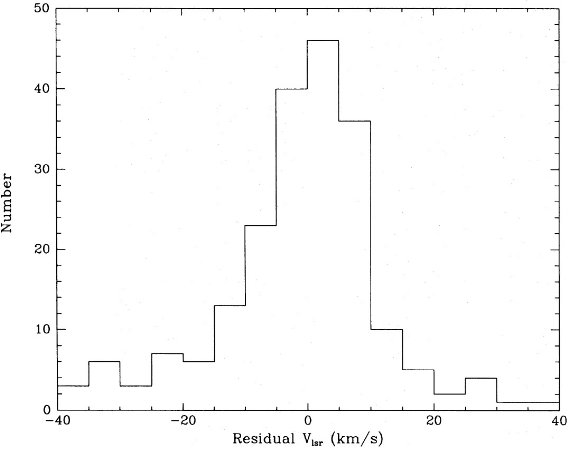 図8.残差速度のヒストグラム。 |
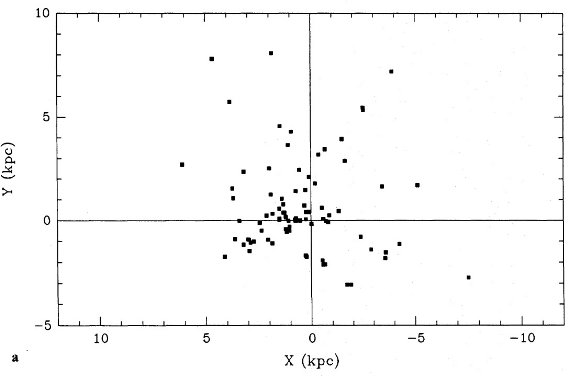 図9a.残差速度 ΔVlsr = [-5, 5] km/s 天体の分布。 |
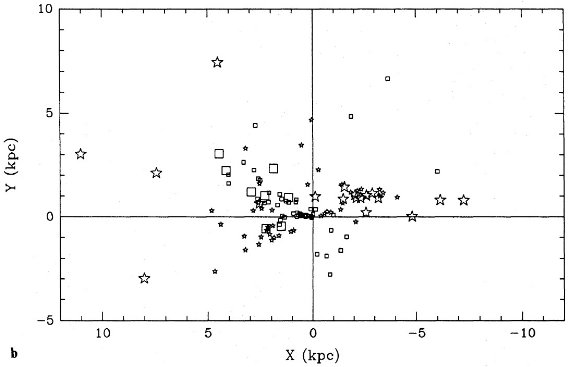 図9b.大星形:ΔVlsr<-20 km/s。小星形:ΔVlsr=[-20,-5] 小四角:ΔVlsr=[5,20]. 大四角:ΔVlsr>20 km/s |
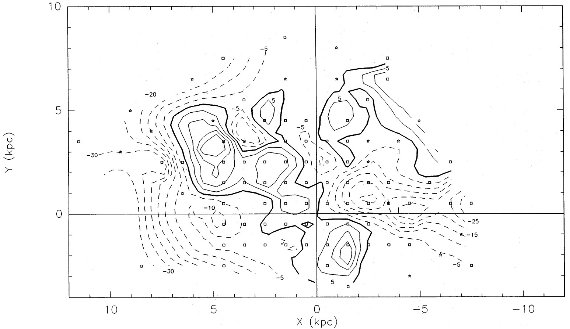 図10.銀河面上に残差速度の分布を示す。データは 1kpc x 1kpc グリッドで 平均化した。 |
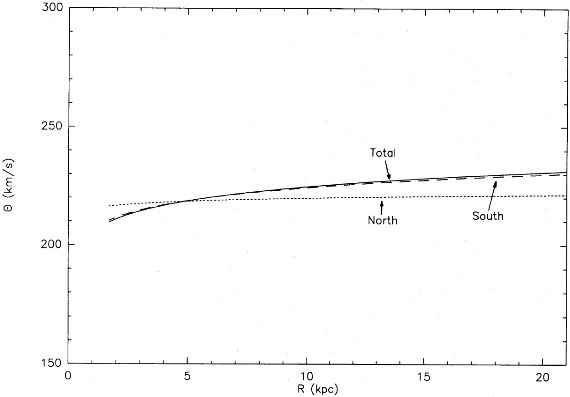 図11.北:l=[0,180] と南:l=[180,360] の回転曲線の比較。 |
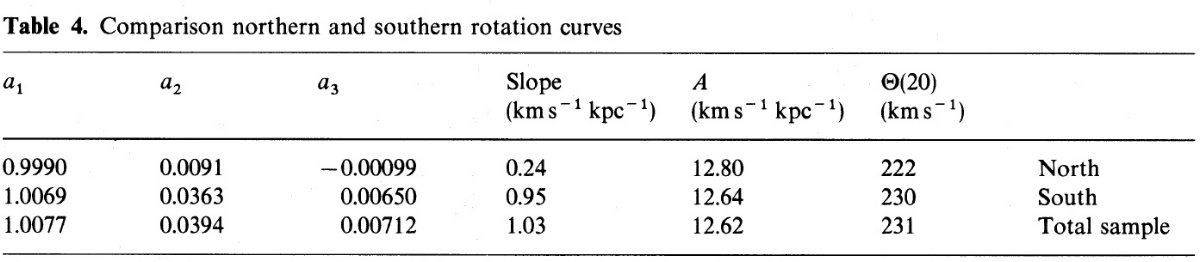
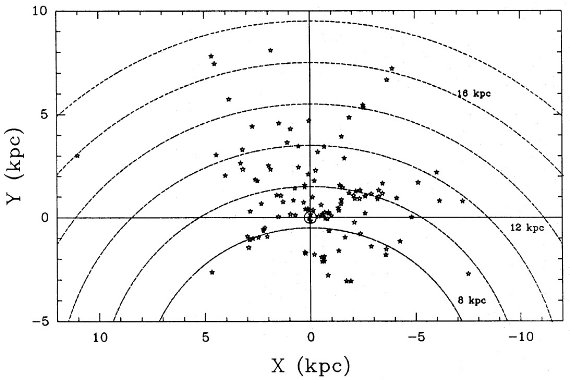 図12.B0 - B0.5 の星を含む複合体の銀河面上での分布。 |
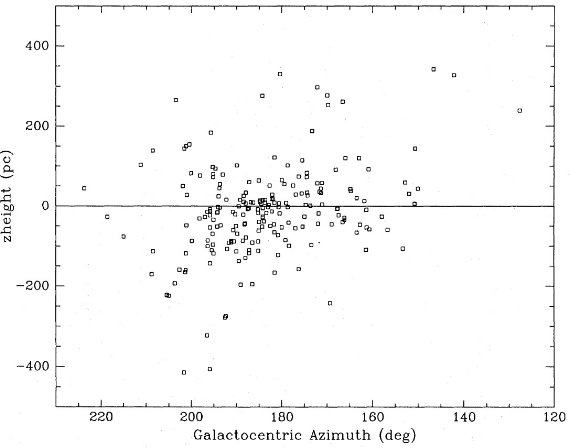 図13.複合体の銀河面光度 Z の銀河中心から見た方位角分布。 ワープのパターンが見える。 |