Low-Mass Stars IV. Carbon Stars


Boothroyd,A.I. and Sackmann, I.J.
1988 ApJ 328, 671-679



アブストラクト

　進化計算が次の組み合わせの星に対し行われた：

　　X = 0.759 Y = 0.24 Z = 0.001　　M = 1.0, 1.2, 2.0, 3.0 M๏
　　X = 0.71 Y = 0.27 Z = 0.02　　　M = 1.2, 3.0 M๏

　レイマースのマスロス式、ロスアラモスのオパシティに低温炭素と分子のいくらかも 含め、主系列から熱パルスまで進化させた。

　古典的ドレッジアップと炭素星形成は２つのケース： Z=0.001, Minit 1.2, 2 M ๏ のみで起きた。
Minit = 1.5 M๏
対流混合距離比 α = 1.5 に増加させた星が Mtot = 1.72 M๏, 11回目の熱パルスで、炭素星になった。その時のピーク強度 log (LHe max/L๏) = 7.86, 核質量 MH = 0.665 M ๏ である。熱パルス後の光度窪みは log (L/L๏) = 3.78 (Mbol = -4.68) である。ドレッジアップ後の Z = 0.0017.
Minit = 1.2 M๏
Mtot = 0.81 M๏の星が α = 3 に増加させた直後 , 第 6 回目の熱パルスで炭素星になった。その時のピーク強度 log (LHe max/L๏) = 7.53, 核質量 MH = 0.566 M ๏ である。熱パルス後の光度窪みは log (L/L๏) = 3.34 (Mbol = -3.59) である。ドレッジアップ後の Z = 0.002.

　α = 1.0 の計算は３次ドレッジアップを起こさなかった。低質量星では α ≥ 1.5 が３次ドレッジアップの必要条件らしい。α が大きくなると 対流層の底部温度が高くなりドレッジアップに好都合となる。その他に、ドレッジ アップに良いのは（１）熱パルス強度：強いほど炭素ポケットを低温側に広げる、 （２）比較的大きな外層質量：対流層の深さ、（３）低メタル量：対流層を深く し、熱パルスを強くする、である。マスロスは熱パルスの回数を厳しく制限する。

１．イントロ　

　早期の理論的研究は M $gt; 5 M๏ でドレッジアップが生じる ことを示したがその結果できるのは大質量、高光度の炭素星のみであった。一方、 観測では炭素星の大部分は低質量、低光度であることが分かった。(Mould, Aaronson 1979, 1982, Blanco, McCarthy, Blanco 1980, Frogel, Persson, Cohen 1980, Richer 1981, aaronson, Mould 1982, 1985) この差は " carbon star mystery " と呼ばれた。

　Weideann, Koester 1984, Aaronson, Mould 1985 の観測データ解析は M > 4 M๏ の星は熱パルス開始前にマスロスで外層を失うことを 示した。

　Castellani et al 1985 は高質量の星ではヘリウム核燃焼期に起きる、セミ対流の "core breathing pulses" が核質量を大幅に増加させることを示した。核質量が 大きいと炭素燃焼が穏やかになり熱パルスが起こらない。彼らの結果は以前考えられ ていたより小さい星質量でも熱パルスの発生を避けられることを示した。対流核に かなりのオーバーシューティングがあると類似の結果が得られることを Bertelli, Bressan, Chiosi 1985 が示した。

　一方、Sackmann 1980 は、外層質量が小さい 星で強い熱パルスが起きると、一回で熱パルス後の膨張により対流層が炭素を 汲み上げて炭素星に変換することを示した。Sackmann はまた初めて炭素による 低温度星オパシティの増加の重要性を指摘した。Iben,Renzini 1982 はその結果 炭素ポケット上端からセミ対流層が新しくできて炭素を上に運ぶことを発見した。 Iben 1983 は古典的ドレッジアップで低質量、低光度炭素星を作った。Wood 1981 はわずか 2 M๏の星にドレッジアップを見出した。

しかし、 これらのすべては勝手に選んだ出発点から計算を始めている。その上、マスロス が入っていないのも大きな欠陥である。 　本論文では、初めからマスロスを入れた進化計算で低質量星の炭素星形成を 調べる。

２．計算の詳細　

　計算は下の組み合わせの星に対し行われた。

　　X = 0.759 Y = 0.24 Z = 0.001　　M = 1.0, 1.2, 2.0, 3.0 M๏
　　X = 0.71 Y = 0.27 Z = 0.02　　　M = 1.2, 3.0 M๏

　計算の詳細は論文IIIを見よ。

．３．結果と議論　

　a) パルス強度の成長　

　パルス強度、すなわちヘリウム光度の最高値 LHemax、は 初め急速に成長する。10 パルスくらい経つと「フル強度」に達し緩やかな増加に 転じる。図１は核質量に対し LHemax をプロットした。 対数でなく実数で見ると、 LHemax は Mc または回数に対し 線形に増加していることが分かる。ドレッジアップがない状況ではこの増加が平坦に なる徴候はない。

　図１から分かるもう一つの重要な点はパルス強度は低メタルでより急に成長する ことである。 熱パルスが強くなるほどドレッジアップに都合がよい。したがって、低メタル星ほど 楽になるわけである。また、ドレッジアップによりメタル量が増加した後では 増加率が鈍るのも理解できる。

　図１を見ると、 LHemax を Mc の関数として表わすのは 困難である。従って、良くやられるように勝手に外層マスを増やしたり減らしたり して、異なる Minit の進化をシミュレートするのは不正確な結果になる。



図１　熱パルス極大強度 LHemax の変化。
　　　実線(Z=0.001), 点線(Z=0.02), 点鎖線(2M๏, Z=0.001, α=1.5)

　b) 炭素星の形成　

　低メタル(Z=0.001)星でドレッジアップへの接近を図２に示した。数パルスの 後、殻間対流の最上端 MCismax は水素ーヘリウム不連続面 MH ≈ Mc から 10-5M๏ の数倍くらいの近さまで下から迫る。 一方、パルス終了からあまり経たない後パルス最高光度期の外層対流層の最下端 MCEmin もやはり、 MH から 10-5M๏ の数倍くらいの近さまで,こちらは上から 迫る。後パルス最高光度期には図２b のように、炭素ポケットの先でセミ対流が 現れる。セミ対流は炭素ポケットが膨張して低温になった際に炭素による オパシティ増加が原因で発生する。セミ対流の底 MSCmin はこうして前回の MCismax より少し下となり、炭素は 領域の頂上 MCismax まで混ざる。

　太陽メタル量の星も同様の振る舞いを示す。しかし、こちらは炭素ポケットの 先でのセミ対流は経験しない。

　α = 1.0 の計算では、外層対流層の最下端 MCEmin は 水素ーヘリウム不連続面 MH から 10-5M๏ の数倍くらいの近さが限界で、それより奥には入れない。そのためドレッジアップは 起きない。Z = 0.001 の場合は図２b, 2c で分かるが、Z = 0.02 も同様である。

　そこで、Z = 0.001, Minit = 1.2, 2.0 M๏ について、α を 変えた計算を行った。



図２a　Z = 0.001 の殻間対流と後パルス外層対流の各パルス毎の振る舞い。
　　　縦軸は対流境界 Mr と水素ーヘリウム不連続面 MH との差　
　　　Mr - MH = 0 は点線で示している。実線は下から、
　　　MHe(ヘリウムが０）,MCbmin(殻間対流の底）、 MCismax(殻間対流の頭）
　　　鎖線はMCEmin(外層対流の底）



図２b　２a の拡大図。MCEminがMCismax の下に侵入するところがドレッジアップ。



図２c　２b をさらに拡大。点線はセミ対流の底MSCminと頭 MSCmax

　i) 1.72 M๏、 Mbol = -4.68　炭素星　

　Minit = 2 M๏, Z = 0.001, Yo = 0.24, Yenv(第１ドレッジアップ後） = 0.257, の星の進化で第９−第１０熱パルス間(Mtot = 1.72)に α を 1.0 から 1.5 へと徐々に上げて行った。図２から見てとれるが、 α = 1.5 では 第１０パルスではドレッジアップに非常に近くなり、第１１パルスでついに実現した。 この時、 Mtot = 1.72, Mc = 0.665 である。また、パルス強度は log ( LHemax/L๏) = 7.86, である。この 一回のドレッジアップで星は n(C)/n(O) = 0.3 から　2.1 の炭素星に変わった。

　また、メタル量は炭素の付加により Z = 0.001 から 0.0017 へ増加した。前パルス 光度は　log (L/L๏) = 3.954 (Mbol = -5.11)である。後パルス 光度窪みの時には log (L/L๏) = 3.782 (Mbol = -5.00) にまで 下がる。論文 I, II からこのメタル量と核質量の星は窪み期が全体の 20 % ある ことが分かる。ただし、その半分つまり 10 % が　 log (L/L๏) = 3.9 (Mbol = 5.0) 以下なのであるが。

　図３は第１１パルス直後の対流の振る舞いを描いている。ドレッジアップの深さは ΔMdredge = 0.00283 M๏ であるが、その内 2 × 10 -5 M๏ だけが C≈0.24 の炭素ポケット物質である。 第１０と第１１熱パルスの間に水素燃焼殻は ΔMH = 0.00643 M ๏ 前進する。だから、λ ≡ ΔMdredge /ΔMH = 0.466 である。

　ドレッジアップの結果起きたメタル量の大幅な増加、外層質量の（僅かだが）低下、 パルス強度の増加率低下などにより、追加のドレッジアップは起こらない。 何でこんな少しの量で組成が変わるんだ？



図３　Z = 0.001, α = 1.5, Minit = 2 M๏ のドレッジアップ (第１１パルス)
　　　実線は対流層境界。点線は水素ーヘリウム不連続面。

　ii) 0.81 M๏、 Mbol = -3.59　炭素星　

　Minit = 1.2 M๏, Z = 0.001, Yo=0.24, Yenv = 0.264 の星で、 第５から第６パルスにかけて α をじわりと 1.0 から 1.5 へと増加させた。 Mtot = 0.81 である。その先は３パルスを α = 1.5 で計算したがドレッジアップ は起こらなかった。そこで、第５パルスに戻り、 α = 2.0 にして、１０パルス まで計算した。その先は外層が消失してパルスが起きない。ドレッジアップはなし。

第１０パルスの時 Mtot = 0.6064 M๏ M&H = 0.6030 M๏ で、Menv = 0.0034 M๏ であったが、 パルス強度log ( LHemax/L๏) = 7.86 はドレッジアップには不足であった。

　そこで、再び第５パルスに戻り、 α = 3.0 で再計算した。すると、次の 第６パルスでドレッジアップが起きた。その時、Mtot = 0.81 M๏ MH = 0.566 M๏ log ( LHemax /L๏) = 7.53 であった。この１回のドレッジアップで、N(C)/N(O) = 0.4 から 3.1 に、Z = 0.001 から Z = 0.0022 に変わった。前パルス光度は log ( L/L๏) = 3.647 (Mbol = -4.35) だったが、後パルスには、 log ( L/L๏) = 3.345 (Mbol = -3.59) に落ちる。

　図４には第６パルス後の対流の振る舞いを描いた。ドレッジアップの深さは、 ΔMdredge = 0.00113 M๏ であるが、その内 6 × 10 -5 M๏ だけが C≈0.26 の炭素ポケット物質である。 第５と第６熱パルスの間に水素燃焼殻は ΔMH = 0.00924 M ๏ 前進する。だから、λ ≡ ΔMdredge /ΔMH = 0.122 である。

　その先のドレッジアップではヘリウムだけが汲み上げられる。しかし、論文II,III で述べた通り、マスロスを半減すると Minit = 1.2 M๏ 星は 第６パルスでは多分 Mtot = 1.0 M๏ 程度で、外層マスは大きい。 外層が先に論じた値くらいに下がる頃までにはパルスは十分強くなっている だろう。すると、α 2.0 の妥当な値でもドレッジアップが起きるであろう。



図４　Minit = 1.2 M๏ Z = 0.001 星のドレッジアップ。α=3


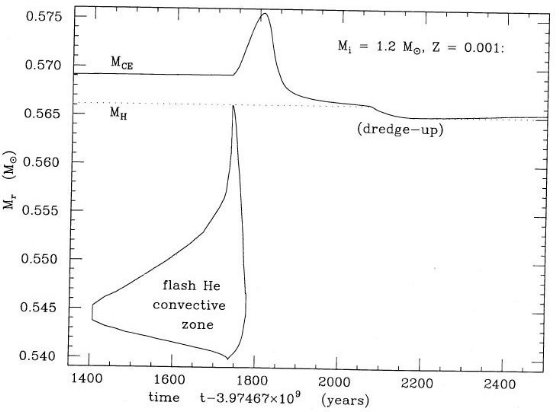
　c) 他の著者による炭素星の形成　

　Sackmann 1980
　Mtot = 0.815 M๏ MH = 0.800 M๏ Z = 0.03 Y = 0.27 α = 1.0 でマスロスなしからスタートした。第２パルスは MH = 0.805 M๏ log ( LHemax /L๏) = 8.2 で後パルス膨張が十分に大きくなった。外層は 0.01 M๏ と小さいため表面対流層は水素ーヘリウム境界を 超えられない。対流底温度は、log T = 4.7 で、質量にして ΔM∼10 -4 M๏ の深さで log T = 7 である。炭素ポケットは 外層と 0.01 M๏ 重なるので、ドレッジアップが起こり、炭素星が 生まれた。Mc が大きいためこの炭素星は明るくて、log (L/L๏) = 4.26 (Mbol = -5.9) である。

　Wood, Zarro 1981
　Z = 0.02 Yenv = 0.30 α = 1.0 Minit = 0.8 - 3.0 M๏ マスロスなし。初めから進化させた。最初の Mc = 0.53 M๏ Mtot = 2.0 M๏ だけ、熱パルスを沢山計算した。この星は Mc = 0.7, 0.8 M๏ からも出発させた。ドレッジアップはなかった。

　Wood 1981
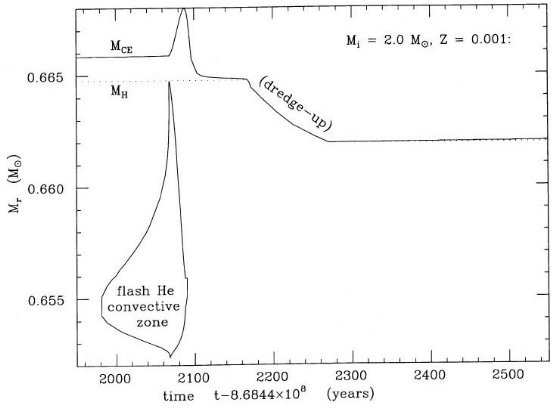
　Z = 0.001 で類似の計算。全て Yenv = 0.30, α = 1.0, MH = 0.55 M๏ から出発。Z = 0.001, Mtot = 2.0 M๏ にはドレッジアップ起こらず。Z = 0.001, Mtot = 1.75 M๏ も同様。 しかし、Z = 0.001, Mtot = 2 M๏ では、MH = 0.674 M๏ (Mbol = -5.2) でドレッジアップが起きた。数回の熱パルス の後炭素星が生まれた。その時、MH = 0.698 M๏ 定性的であるが、Z を下げる、α を上げるとMtot が小さくて、 Mc が小さくてもドレッジアップが起きることを示した。

　Iben 1982
　Despain は M = 0.6 M๏、マスロスなし、Z = 0.001, Yenv = 0.25, α = 1.5 の星を水平枝から中心でヘリウムが無くなるまで進化させた。Iben はそこから出発し、AGB 上で熱パルスを何回か起こさせた。第７と第８パルスの間に じわじわと外層に 0.1 M๏ 注入して M = 0.7 M๏ とした。そこからさらに５回のパルスを追った。最後の第１２パルスでは M H = 0.612 M๏ となった。
　Iben, Renzini (1982a,b) はそこから第１３パルスを追い MH = 0.624 M๏ で改良された炭素オパシティを入れ、ドレッジアップを起こした。 ΔMdredge = 2 × 10-4 M๏ で、 n(C)/n(O) = 5.6 となった。
　Iben, Renzini (1982b) は低温炭素オパシティをさらに改良し、第１２パルスから 第１４パルスまで再計算し、第１３、第１４パルスでドレッジアップを得た。
第１３パルスは、MH = 0.624 M๏ log ( LHe max/L๏) = 8.003 n(C)/n(O)=2.3であった。 第１４パルスは、MH = 0.624 M๏ log ( LHe max/L๏) = 8.142 ΔMdredge = 4.2 × 10-4 M๏ n(C)/n(O)=5.2 となった。
これらのモデルではセミ対流が外層底に存在し、ドレッジアップに際して水素を下に 送り込んでいた。


　Iben 1983
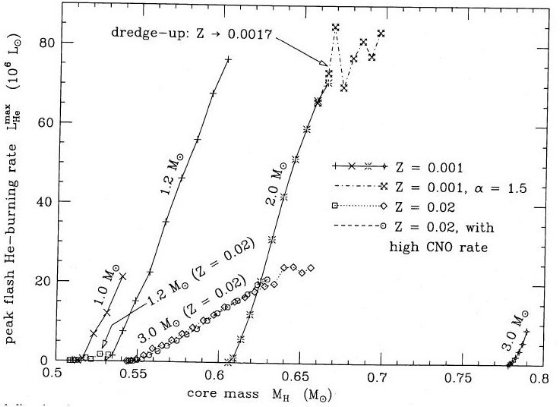
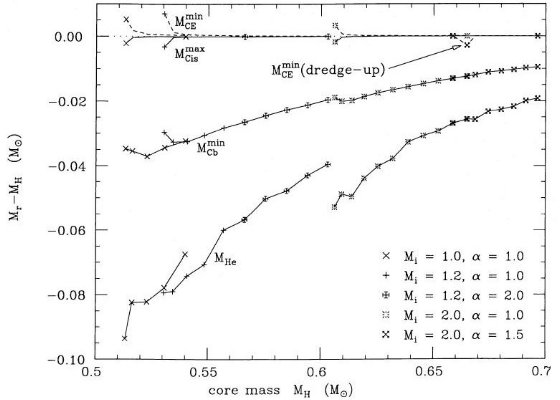
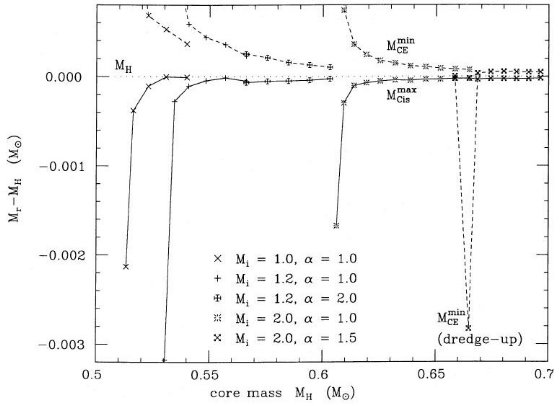
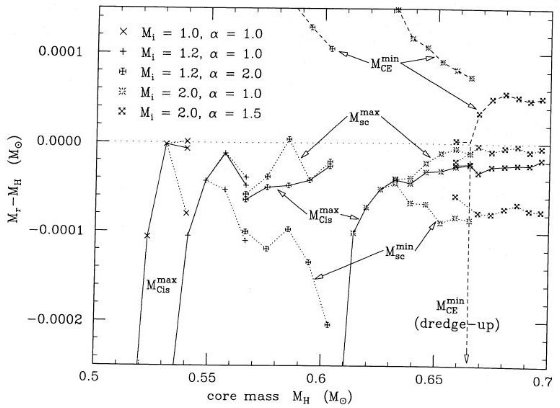
　Iben 1983 は、Yenv = 0.25, Mc = 0.58 から 0.65 M๏ について、 Z、Mtot, α を変化させて計算を繰り返した。どうも、同一のIben 1982 コアの 上に色々な外層を乗せて計算したらしい。全ての場合でドレッジアップが最大の 時パルス強度は、log ( LHemax/L๏) = 8、 MH = 0.63 M๏ であった。
Mtot = 0.7 M๏ Z = 0.001, &alphaIben=1.0, 1.5 の時、 ドレッジアップ、炭素星形成が起きる。Mtot = 1.0, Z = 0.001, &alpha Iben=1.5 ではドレッジアップが早く起き、もっと多数持続した。Mtot = 1 M๏ Z = 0.02, &alphaIben≤1.0 ではドレッジ アップは起こらなかった。&alphaIben = 1.5 ではドレッジ アップは起きたが、Ｚが大きいため炭素星まで至らない。

　Hollowell 1986, 1987
　HollowellはIben 1982 のモデルから出発した。Mtot = 0.7 M๏ Z = 0.001, Yenv = 0.25 &alphaIben = 1.5 である。彼はその第９ パルスから、マスロスなし、対流の拡散近似を使った計算を第１６パルスまで行った。 オーバーシュートなしの計算ではドレッジアップは起きなかった。オーバーシュート ありの時ドレッジアップと炭素星形成を第１４パルスで得た。MH = 0.639 M๏ log ( LHemax/L๏) = 8.15 λ = 0.01 であった。第１５パルスも似たような結果であるが、第１６ パルスはドレッジアップ量が大きく減少している。

　Lattanzio 1986, 1987
　Lattanzio は主系列からマスロスなしで進化させた。Z = 0.001, 0.01, 0.02, Y = 0.2, 0.3, α = 1.0 Minit = 1.0 から 3.0 M๏ である。これらは 最初の熱パルスまで計算された。
　Minit = 1.5 M๏ モデルは 5 - 10 パルスまで計算したが ドレッジアップはなかった。次に Minit = 1.5 M๏ Z = 0.003, 0.006, Y = 0.20, 0.30, α = 1.5 を計算した。(Y, Z) の４つの組み合わせの それぞれを主系列から進化させ、ヘリウムフラッシュは「ジャンプオーバー」させて、 熱パルスを経過させた。(Y,Z) = (0.20, 0.006) モデルは１３パルスでドレッジ アップなし。(0.30, 0.006) モデルは２３パルスを計算し、第２３パルス, MH = 0.7 M๏, Mbol = -5.5, M(post-pulse) = -4.9 で かすかなドレッジアップが起きた。(0.30, 0.003) モデルは２６パルスを計算し、 第１９パルス、MH = 0.69 M๏, Mbol = -5.4で 最初のドレッジアップを起こした。第２６パルスまでに n(C)/n(O) は 0.293 から 0.6 に増加した。(0.20, 0.003) モデルは第１７パルスまで追い、第１１パルス、 MH = 0.62 M๏, Mbol = -4.8 で最初のドレッジアップ を起こし、第１７パルス、MH = 0.65 M๏, Mbol = -5.2 窪み Mbol = -4.4 で炭素星となった。第１７パルスでは ΔMdredge = 2.86 × 10-3 M๏ λ = 0.38 であった。





．４．結論　

　Iben,Renzini 1982 がセミ対流が重要であると言ったが、彼ら自身の計算でそれが 効くのは実際には水素を下に送り込むドレッジダウン効果だけであることが分かった。
　低質量星でのドレッジアップのためには、α ≥ 1.5 が必要なようである。 α = 1 でドレッジアップを得たのは Wood 1981 のみであり、それもかなり 大きな Mtot ≈ 2 M๏ でのことである。注意すべきは、 α は対流層の質量としての深さは殆ど変えないが、温度で見ると大きく 変わるという点である。質量で変わらないのは対流層の底が核のすぐ外側まで接近 しているからである。温度の方はそこで log T = 7 から 4.5 まで変わり得る。 4.5 って本当か？　　密度、半径も同様である。
　本論文でドレッジアップが起きたか起きかけたケースは以下の４つであった。
（１）Minit = 2.0 M๏　Z = 0.001, α = 1.5 Mtot = 1.7 M๏ MH = 0.67 M๏ での
　　　第１０，１１パルス。
（２）Minit = 1.2 M๏　Z = 0.001, α = 3.0 Mtot = 0.8 M๏ MH = 0.67 M๏ での
　　　第６，７パルス。

　これらのどれもで、表面対流層が最も深く侵入した時、つまり MCE = MCEmin の時に、対流層の底の温度が全て log TCEmax = 6.5 であるのは偶然の 一致ではないだろう。異なるMtot でドレッジアップを起こすのに大きく異なる α を必要としたのだが。これは、異なる α は、単に対流層の底が ある特定の温度 TCEmax に到達するために必要であった に過ぎないことを示唆する。ただし、その温度が他のパラメターに依らない普遍的な 値とは思えないから大きな助けとも思えないが。
　α を決めて TCEmax を確定する試みもとても簡単 とは言えない。

　ただし、ドレッジアップに対するある他のパラメターの影響を TCE max と関連付けることは可能である。例えば、外層マス Menv の減少は TCE の減少につながる。そして、確かに計算結果では外層 マスが減少するとドレッジアップが起きにくい。小さい外層マスは他の効果例えば 大きい α とか、強いパルス強度などで補償されなければならない。

　大きな Z もやはりドレッジアップの邪魔になる。実際 Z = 0.02 Minit = 3.0 M๏ α = 1.0 の 第２０パルスの TCE は、 Z = 0.001,Minit = 1.2 M๏ α = 1.0 の第１１パルスと 較べると、１/４である。両者は良く似た Mc と　Menv を持っていたが。
　高い Z が邪魔をするもう一つの理由は、図1からも分かるように、パルスピーク 光度 LHemax の成長が低 Z では,高 Z よりずっと速いの である。多くの仕事がドレッジアップには十分に強いパルスが必要であることを 示している。

　ドレッジアップを起こすとその後の LHemax は 増加が鈍るか、場合によっては下がることが Iben 1983, Hollowell 1987, 本 論文で観察された。これはおそらくドレッジアップによる Z の増加が原因であろう。 ただし、ドレッジアップが停止してしまう場合もあり、これは　Z 増加に加え、 外層マスが減少したことが原因と考えられる。