アブストラクト3 M๏ ≤ M ≤ 9 M๏ で確立している Mcore - L 関係を 0.8 M๏ ≤ M ≤ 3 M๏ まで拡張した。RGB と AGB のそれぞれに Mcore - L 関係が得られた。進化計算 ではレイマースのマスロス式を適用した。RGB では Z=0.02 の時 0.3 M๏ ≤ M ≤ 0.45 M๏ で L = (6.86 Mc)7, Z 依存性は、L ∝ μ7(ZCNO )1/12 である。 AGB ではZ=0.02 の時 0.52 M๏ ≤ M ≤ 0.7 M๏ で L = 52000 (Mc-0.456)、 Z 依存性は、L ∝ μ3(ZCNO )1/25 である。 低質量 AGB 星に対する Mc-L 関係は Mc 質量の大きい領域で決められた関係より 緩くなる。熱パルスサイクルで光度が変動するため Mc-L 関係からのズレが おきる。この論文ではその確率を計算した。低質量星では |
（１）水素燃焼率の変化は影響が小さい。 （２）対流混合距離の不確定さによる影響は無視できるほど小さい （３）星の総質量の影響は小さい。 １．イントロこれまで、Mc - L 関係は AGB 星に対して求められてきた。この段階の計算は 計算の容易さから主に 3 M๏ ≤ M ≤ 9 M๏ で行われてきた。しかし、観測的にはもっと低質量な星が主役である。そのような 低質量星に対してはまだ Mc - L 関係が確立していない。この論文の目的はそこに ある。M ≤ 2.5 M๏ の星ではヘリウム核燃焼が縮退条件で起きる。 このヘリウムフラッシュの計算は難しいため、普通は水平枝から進化計算を始めて いる。しかし、この論文では主系列から始めて多数の熱パルスまで追跡した。 |
２．過去の仕事Paczynski AGB 星の Mc - L 関係は Paczynski 1970 が発見した。その時の計算は M = 3, 5, 7 M๏ で、X=0.70, Y=0.27, Z=0.03, ZCNO = 0.015 であった。平均分子量 μ ≈ 4/(5X+3-Z) = 0.618 である。計算 に使用した対流の混合距離比 α = (l/H) = 1 を採用した。計算は主系列から AGB まで行い、熱パルスはヘリウム燃焼殻と水素燃焼殻の間隔を強制的に一定値に 保って抑えた。その結果下の関係を、0.57 M๏ ≤ MH ≤ 1.39 M๏ に対して得た。L = 59250 MH - 30950 = 59250(MH-0.522) Iben Iben 1977 は、M = 7 M๏, X = 0.70, Y = .28, Z = 0.02, μ = 0.617 の星を主系列から AGB 上 18 回の熱パルスまで計算した。そこでは、 MH = 0.96 M๏, 外層では第１、第２ドレッジアップ のため X = 0.6378, Y = 0.35, Z = 0.0122, μ = 0.648 となっているが、 オパシティは Z = 0.02 のまま計算している。注意しておくべきは彼のα = (l/H) の定義が他の半分としていることである。彼の計算で α = 1.0, 0.7 となっているのは α = 1.8, 1.3 と読み変えなければいけない。Paczynski 1970 と似た手法で熱パルスを抑えて、彼は星を MH = 1.16 M ๏、次に MH = 1.36 M๏ まで進化させた。 最後の２点では彼は熱パルスの抑制を解き、熱パルス間進化を追った。彼は 次の関係を導いた。 L = 59,000 ( MH - 0.38 ) この関係は 0.96 M๏ ≤ MH ≤ 1.36 M ๏ で成立する。彼は後にこの式を改訂(Iben,Truran 1978)し、 星の総質量とへの依存を見出した。これは主に彼が 大きな星質量と大きな対流の混合距離比を使用しているためでもある。 Tuchman, Glasner, Barkat 1982 が指摘するように、大きな全質量 M と大きな対流の 混合距離比 α は対流層を燃焼殻近くまで深め、Mc - L 関係に影響する可能性 がある。したがって、Iben が考察したように質量が大きい場合、Mc - L 関係は 全質量や対流の混合距離比の依存性が存在する。しかし、低質量星ではその依存性は 弱い。 Havavelet, Barkat Havavelet, Barkat 1979 では最初のヘリウム殻パルスが星の全質量に対して 以下の核質量で起きている。初期組成は, Xo=0.70, Yo=0.29, Z=0.01 で ZCNO=0.0014 （やや小さい）である。α には触れていないが多分 α = 1 - 1.5 であろう。
計算の詳細には触れていないが幾つかの進化計算 は数回の熱パルスを経過して Mc - L 関係として、MH ≥ 0.6 で L = 65,000 ( MH -0.525) Becker, Iben 1980 は文献から採った間パルス光度と核質量をプロットしている。 しかし、その間の違いなどを調整することはしていない。 |
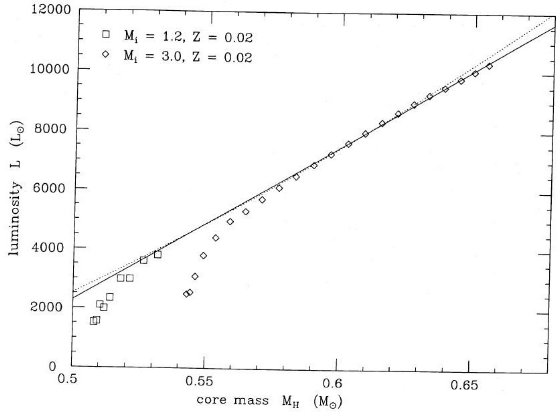
Wood, Zarro Wood, Zarro 1981 は X = 0.68, Y = 0.30, Z=0.02, μ = 0.627, M = 0.8, 1.0, 2.0, 3.0 M๏ で書いていないが多分 ZCNO=0.01 の星を α = 1 で扱った。彼らは MH 0.53, 0.7, 0.8 M ๏ に対して、熱パルス直前の状態を再現するように幾つかの人工的な出発 モデルを作った。そこから進化計算を行い、0.6 ≤ MH ≤ 0.9 に 対して、次の Mc - L 関係を得た。全質量依存性はない。 L = 59,250 ( MH -0.495) Iben, Renzini の総括 Iben,Renzini 1983 の総括では幾つかの Mc - L 関係が紹介されている。Wood,Zarro 1981 の式は低質量星用として、中間質量星に対しては Iben,Truran 1978 から L = 63,400 ( MH -0.44)(M/7)1.83 ただし、指数は「Paczynski 1970, Uus 1970と合わせるため」半分になっている。最後に 広い範囲で使えると紹介されたのは Iben 1981 からで、 L = (59,250 + 4150 x )( MH - 0.495 0.0505 x) ここに、x ≡ [(M - MH)/6.04]1.83 Lattanzio（出版後） この論文が完成した後に Lattanzio 1986 が出た。彼は M = 1.5 M๏ , Y = 0.20 と 0.30, Z = 0.001, 0.01, 0.02, ZCNO=0.6 Z, α = 1 の進化を主系列から熱パルス 5 - 10 回まで計算した。種族Ｉの星 では、0.55 M๏ ≤ MH ≤ 0.6 M๏ で L = 55,320[ 2.3 ( Y - 0.20 ) + 1.0 ]( MH - a ) ここに、 a ≡ 0.489 + 0.23 ( Y - 0.20 ) - 0.70 ( Z - 0.02 ) 低メタル(Z = 0.001)の場合は、0.6 M๏ ≤ MH ≤ 0.65 M๏ で L = 51,800[ 4.7 ( Y - 0.20 ) + 1.0 ] MH - 26,260 [6.2(Y - 0.20) + 1.0] ただし、計算パルス数が足りないので勾配の不確定性は大きい。 Refsdal, Kippenhahn の半解析的手法 他の研究者(Refsdal, Weigert 1970, Kippenhahn 1981)は半解析的手法を取った。 Kippenhahn は核が小さい時光度が組成に強く（L ∝ &mu:7）依る とし、核質量が大きくなると輻射圧の影響が強くなり &mu: の効果は弱くなるとした。 Tuchman, Glasner, Barkat 1983 は Mc - L 関係をより透明で一般的な形で 扱おうと試みた。彼らの単純化の結果は、水素燃焼殻の上での光度をその点での 温度、核質量、外層組成に関係付ける二組の方程式にまとめられた。原理的には この式から光度を核質量とＺの関数として導ける。 |
３．計算の詳細計算は次の組み合わせの星に対し行われた：X = 0.759 Y = 0.24 Z = 0.001 M = 1.0, 1.2, 2.0, 3.0 M๏ X = 0.71 Y = 0.27 Z = 0.02 M = 1.2, 3.0 M๏ 注意しておくが、赤色巨星枝上での第１ドレッジアップは外層ヘリウム量を ΔY = 0.01 増加させ、水素を同じだけ ΔX = 0.01 減少させる。 α = 1.0 である。α ≥ 2 は現実的でないが、いずれにせよ 光度には殆ど影響しない。 Teff < 5000 K では Reimers 1975 のマスロス式を適用した。最新の Los Alamos オパシティ(1985) が使われた。計算の詳細は論文ＩＩＩ。 図１ CNO 燃焼率の Mc - L 関係への影響。新しい反応率は前の３−４倍 だが、 Mc - L 関係では 4 % しか影響がない。 |
|
|
a) RGB 上での Mc - L 関係 ヘリウムフラッシュ以前の RGB 星でも Mc - L 関係が存在すると指摘したのは Refsdal, weigert 1970 と Kippenhahn 1981 である。彼らの式は、 L ∝ μζMHφ (MCNO)ξ で、ζ≈7, ξ ≈ 8 であり、多分 0 < ξ ≤ 1。上の 式は我々の直接モデル計算の結果とも一致する。低質量星は上の式に乗る前に 一度 RGB の窪みを経験する。驚くことに、窪みの前でもかなり良く式に乗って いる。 Z=0.001と0.02の計算 図２では、Minit = 0.8, 1.0, 1.2, 2.0 M๏, Z = 0.001, Z CNO = 0.00075, μ = 0.598 に対する Mc - L 関係 が描かれている。近似 式は、
 図２ Z = 0.001, μ = 0.598 での RGB 星の Mc - L 関係 | 太陽組成 Z=0.02, ZCNO = 0.015, μ = 0.624 に対する Mc - L 関係 は 図３のようで、下の近似式でフィットされる。この式はKippenhahn の式と一致する。
組成効果の表現 二つの組成に対する式の定数 412,000 と 714,000 は組成効果とみなせる。Kippenhahn に習い、L ∝ μ7 を式の中に含めておくと、 (0.598/0.624)7(0.00075/0.015)ξ ≈ 412,000/714,000 から、ξ ≈ 0.084 ≈ 1/12 を得るので、 0.3≤MH≤0.45 での統一式として、 L=2.91×107(ZCNO)1/12μ7 MH7=(11.6μMH)7(ZCNO) 1/12  図３ Z = 0.001, μ = 0.598 での RGB 星の Mc - L 関係 |
|
L の定義
Mc - L 関係に使う L は、熱パルス前の間パルス極大光度を使用する。この時ヘリ
ウム殻燃焼は極小を示す。 これまでの結果 図４でこれまでの Mc - L 関係を比較した。どの星でも最初のパルスは低い光度で 起きる。５−６回の後には間パルス光度は Mc - L 関係光度に接近する。例外は M = 3, Z=0.001 のケースで数回後にまだ関係光度から離れている。これは Mc=0.79 とここ で扱っているMc より遥かに大きく関係光度に接近するのに回数がかかるためである。 組成に依る違い、低質量と高質量での傾きの違いが見て取れる。 また、太陽組成では Z=0.001 に較べ遥かに低いMc で最初の熱パルスが開始する ことを注意しておく。 Z=0.001, 0.02 の計算 下の図５に示す Z=0.001 で低核質量 (0.5≤ Mc ≤0.7)に対する近似式は
Z=0.02 (図６)の場合は次の式でかなり良くフィットする。 L=52,000(MH-0.456) 0.52 ≤ MH ≤ 0.70 (3000≤L≤12,000) (15) 組成効果の表現 組成依存を組み込むのは難しいが、結局下式になった。 L=238,000μ3(ZCNO)1/25(MH 2-0.0305MH-0.1802) 0.5≤MH ≤0.66 (16) この式をMHに対して書き直すと、2000≤L≤10,000に対して下の (17)式を得る。
 図５ Z=0.001 の Mc - L 関係 実線は(14)式、点線は(16)式 |
 図４ Mc - L 関係の比較。 HB:Havazelet,Barkat 1979, WZ:Wood,Zarro 1981, I7, I1:Iben et al for 7,1 Mo, L1:Lattanzio Pop I, L2:Lattanzio Pop II  図６ Z=0.02 の Mc - L 関係 実線は(15)式、点線は(16)式 |
|
他との比較 右（図７）は(16)式を計算データと比較した図である。Z=0.001データと重ねるため Z=0.02データは0.8倍してある。Kippenhahn 1981 による、MH が上がると Z 依存性が弱まる、という予言の通り、MHの高い部分で Z=0.02 点は (16)式線より少し下になってしまった。これは(16)式がＺ依存をMHに 無関係に一様に表現しているためである。 図７ではまた、以前発表された関係式を(16)式の組成依存で調整してプロット した。Iben 1977 だけは高いMHを扱っていて Z 依存が異なるので 載せていない。図を見るとこれまでの関係式が全て(16)式の下に来ることが分かる。 これはそれらの研究が大きな MH で行われ、そこでは関係が非線形 になっていることが一因である。また、Paczynski 1970 では間パルスの最高光度 でなく平均光度を使っているためファクター 1.2 のズレを生んでいる。ただ、 Wood,Zarro 1981 のずれは説明しにくい。 光度変動の確率分布 最後に大事な点が一つ：間パルス期の光度は（１６）式より低い値に留まる 確率がかなり高い。熱パルス１サイクル間の最高と最小光度は、Mc - L 関係で 定義された L (熱パルス前の間パルス極大光度) と較べ、その２倍、1/2 倍の変動を 示す。従って、Mc - L 関係は、Mc に対して L の確率分布を与える関係式で置き換え られるべきである。 図８、図９は Z=0.001 と Z=0.02 で、あるMc-L関係光度Lm に対する光度累積確率 一定の線を示す。光度変動は Mc だけでなく星の総質量 Mall にも関係するはずである。 しかし、論文 I に示したように、パルス後の非常に短い光度の窪み以外は目立った違い は現れない。重要な部分、つまり Mc - L 関係線以下での光度確率分布は Mc と Z に のみ依存すると言える。 この光度変動は、光度観測から Mc を推定する場合 (Weidemann 1984, Aaronson, Mould 1985) に重大な影響を及ぼす。例えば、 Mc = 0.6 M๏, Z = 0.001 の星を観測した時、3100 L๏<L<4200 L๏ である確率が 10% あり、その結果 M๏< Mc < 0.557 M๏ と看做してしまう。0.589 M๏< Mc < 0.609 M๏ と評価する確率は 67 % である。このように、過半の星ではその 光度が Mc - L 関係に従っているが、それよりかなり低い光度にある確率は無視できない。 逆に関係光度以上にある確率は 2 % 程度である。 AGB 先端付近ではこの状況はもう少し良い。先端近くの星が１個か２個だった時、それが Mc - L 関係の光度である確率は高い。勿論、総数が小さい星団  図８ Z=0.001 の熱パルスによる L 変動を示す Mc-L 確率。中央実線は(16) 式の Mc-L 関係。上側点線の数字は、Lがその線の上である割合(%)。 下側点線の数字は、Lがその線の下である割合(%)。 |
 図７ Z=0.001, 0.02 の AGB Mc-L プロット。Z=0.02データはZ=0.001データと 重なるよう 0.8 倍にしてプロットした。実線：(16)式。点線は、 P：Paczynski 1970を0.782倍, WZ:Wood,Zarro 1981を0.761倍, HB:Havazelet,Barkat 1979 を0.868倍 では、先端光度付近に 星が存在しない可能性が高く、それが先端光度見積もり値を大幅に引き下げる原因となる。 それが、Aaronson,Mould 1985 の図４で幾つかの点が低い原因であろう。 その点で、Aaronson,Mould 1985 が彼らの図４から図５に移る際に、Iben, Renzini 1983 のMc-L関係を用いている点を注意しておく。ただ、もし本論文の（１７）式を用いても それによる補正はデータの分散以下である。 図９ 図８に同じ。Z=0.02 |
５．結論（１）RGB の Mc - L 関係は Refsdal,Weigert 1970, Kippenhahn 1981 の予言と合う。 計算データへのフィットが L ∝ MH7 となり、; ∝ MH8 でなかったのは、本論文では Mc ≈ 0.4 M๏ と高めの Mc を扱ったためであろう。組成比の影響は あまりはっきりしない。（２）AGB の Mc - L 関係は Tuchman, Glasner, Barkat 1983 の予想と合い、低Ｍｃ では勾配が緩い。本論文とWood,Zarro 1981 （Mc ≈ 0.65 M๏） の間には |
組成比の違いを考慮しても 10 % の差がある。これは、多分組成比依存性がMcで異なる結果と思われる。 （３）（１６）、（１７）式は Mc ≤ 0.65 M๏ の低質量領域 で適当である。高質量側で直線フィットすると、Mc=0.5でＬ＝０となってしまうので 非線形性に注意。 （４）本論文は、Mc - L 関係に星の総質量依存は検出されるほど強くないという点で、 Paczynski 1970, Wood,Zarro 1981 と一致する。 |