Bladh19

The Evolution of DARWIN; Current Status of Wind Models for AGB Stars

Bladh

2019 "Why Galaxies Care about AGBs?",

　アブストラクト　

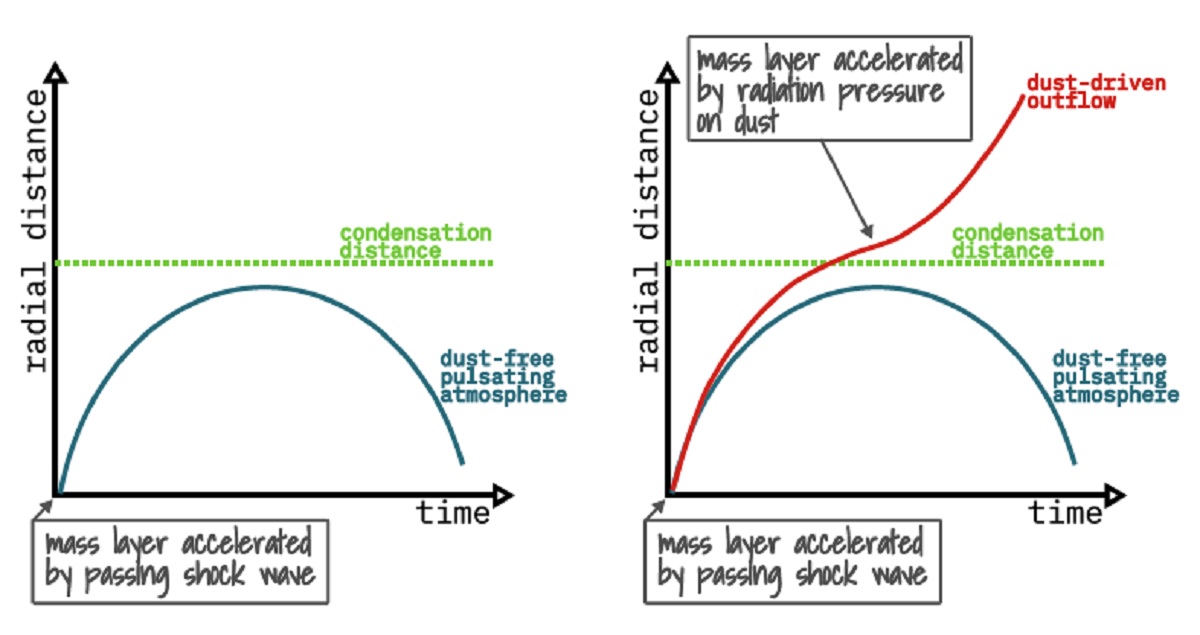
　AGB 星の低速で濃い風の原因は動的な大気内でのダスト形成と輻射圧との結合に帰せられる。

　DARWIN コードによる計算は、C-リッチ、O-リッチ星の両方で、観測に合う星風を作ることに成功した。ここに DARWIN モデルの概要を示す。

　１．イントロダクション　

図１．星風の２段階の図示。左：ダスト形成なしの場合。右：ダスト形成ありの場合。

　２．ダーウィンコード　

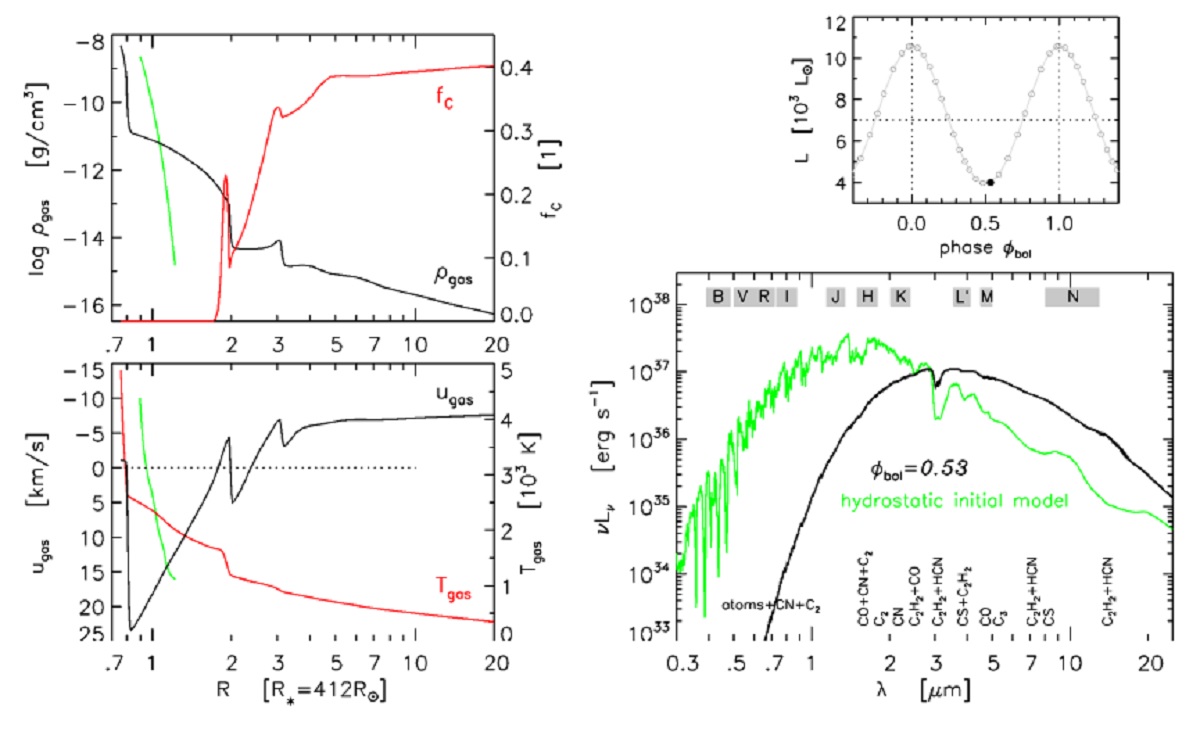
　コードの中身　

　DARWIN=Dybamic Atmosphere and Radiation-Driven Wind model based on Implicit Numerics

流体力学方程式＋波長依存の輻射方程式＋時間依存のダスト成長を解く。
内側境界＝光球面の直ぐ内側。　外側境界＝25 R*
初期モデル＝静的平衡大気。
脈動＝内側境界を次第に振幅が増すサイン関数型で揺らす。

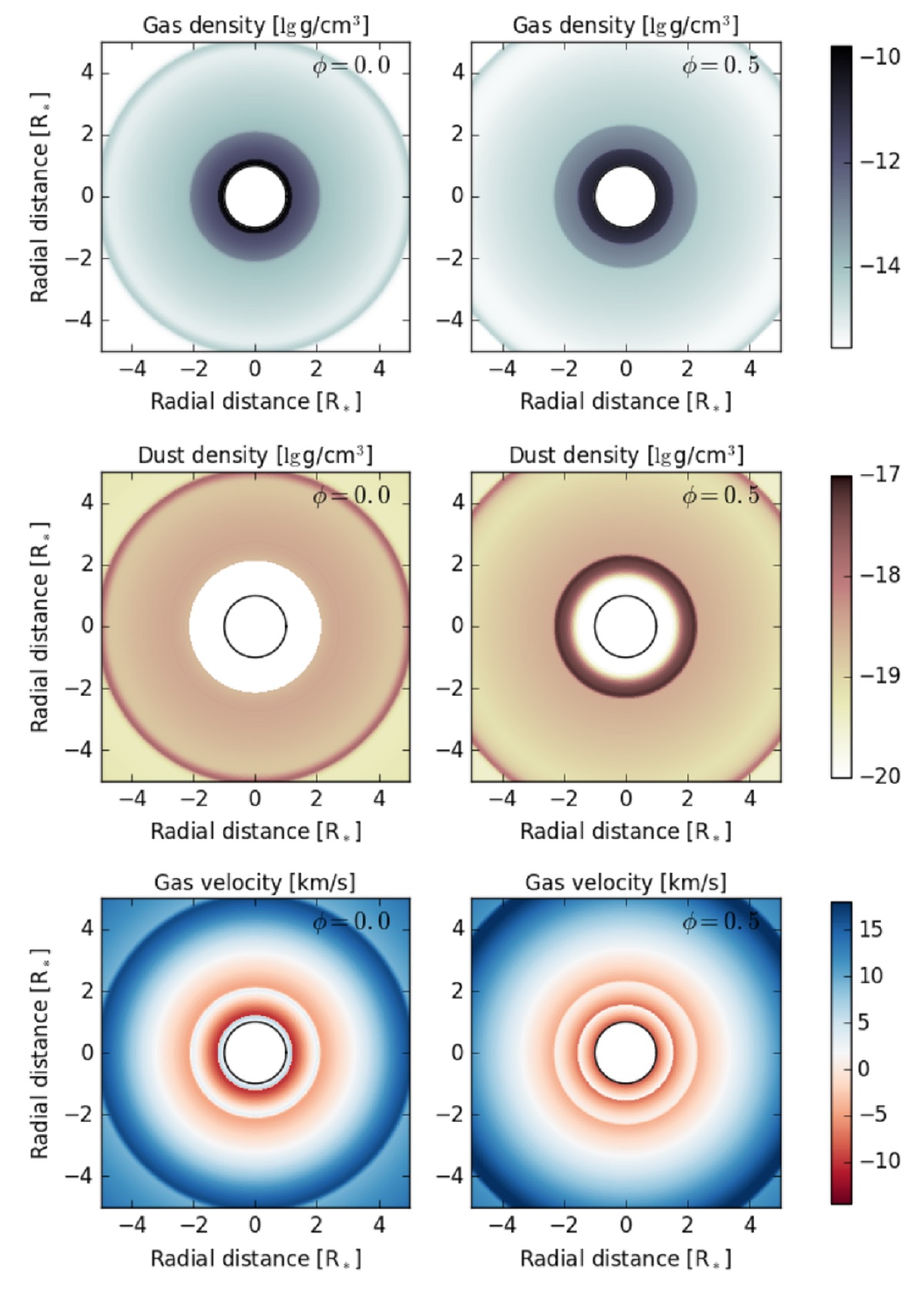
　図２＝極大と極小時の断面図　

　Hofner et al 2016　

　ダーウィンコードの詳しい説明は Hofner ey al 2016 を見よ。観測との比較は Nowotny et al 2010, 2011, Eriksson et al 2014, Bladh et al 2013, 2015 を見よ。

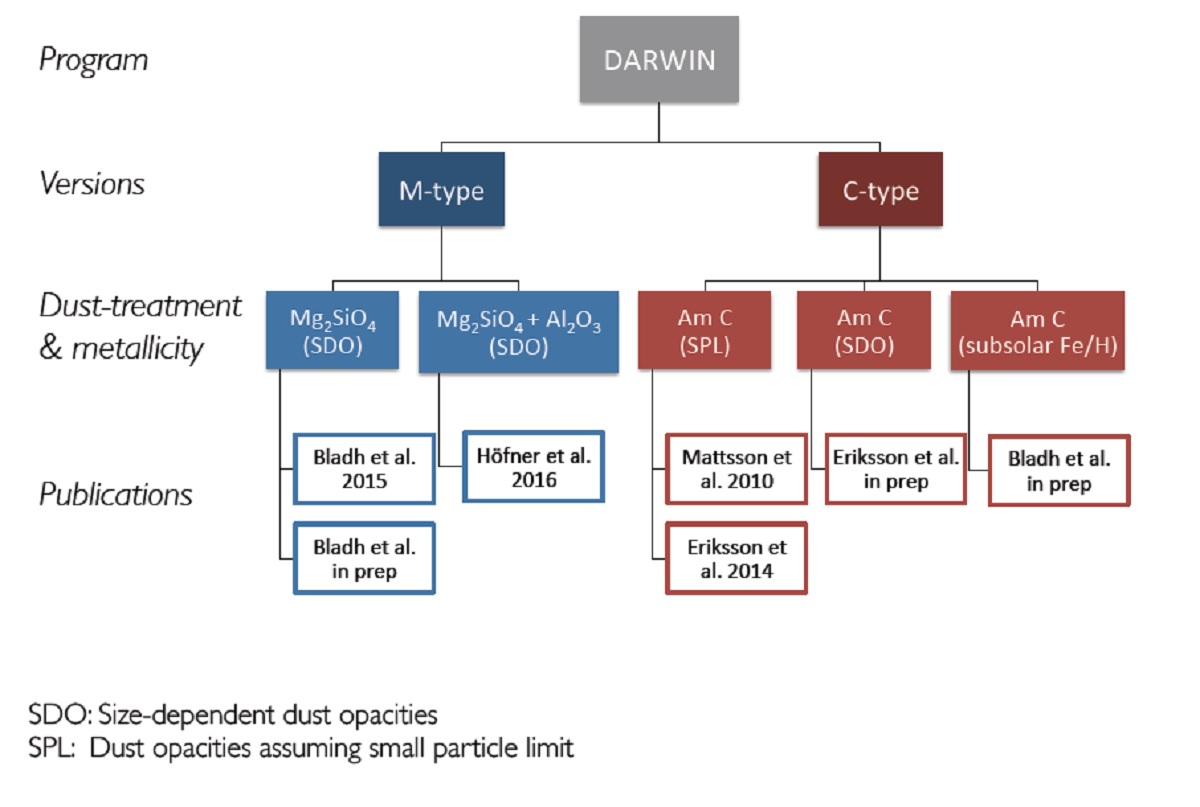
図２．炭素星(1Mo, 400 Lo, 2600K, u_p 2km/s, [Fe/H]=-1.0)のガス密度、ダスト密度、ガス速度の断面図。左：φ=0.0(極大)。右；φ=0.5(極小)。黒丸＝恒星表面。

　３．様々なダーウィンモデル　

　炭素星モデル　

第１モデル
　ダスト半径 << 波長ーー＞吸収＝小粒子近似

第２モデル
　サイズ依存の吸光計算。Mattsson et al 2010 に炭素星の大規模グリッドが与えられている。マスロスも。ダーウィンコードによるより小さいグリッドが Eriksson et al 2014.

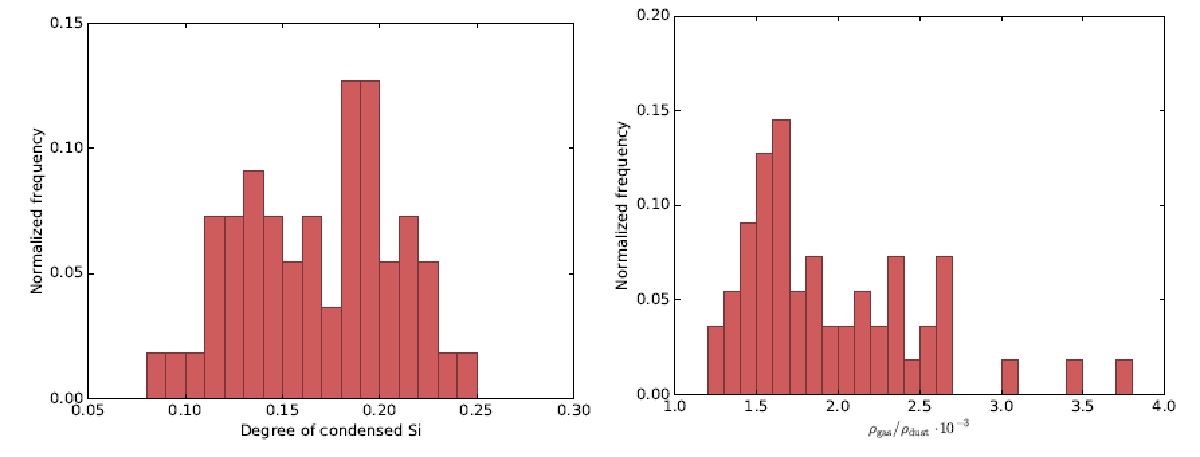
　M-型星モデル　

　酸素リッチな環境での核形成はまだ不確実なので、M-型星では種粒子を与える。吸光はサイズ依存で計算。これは散乱で駆動される星風では必須である。 M-型星グリッドは Bladh et al 2015 が与えたが 1 Mo に限定された。より広範なグリッドは Bladh et al 2018 が与える。
第１モデル
　Mg₂SiO₄ 粒子の時間依存成長。Fe は考えない。

第２モデル
　Al₂O₃ 粒子の時間依存成長も加えた。 Al₂O₃ 粒子はグレイン核を提供し、その周りに Mg₂SiO₄ が積もる。

図４．現在までに出版去れたダーウィンモデル。

図５．ますろすの時間変化。色付き部は最初の振幅増大期で無視すべし。左：炭素星。右；M-型星

図６．ダーウィンモデルサブセットから採った左＝Si の個体率と右＝ダスト/ガス比のヒストグラム。

　４．ダーウィンモデルの結果　

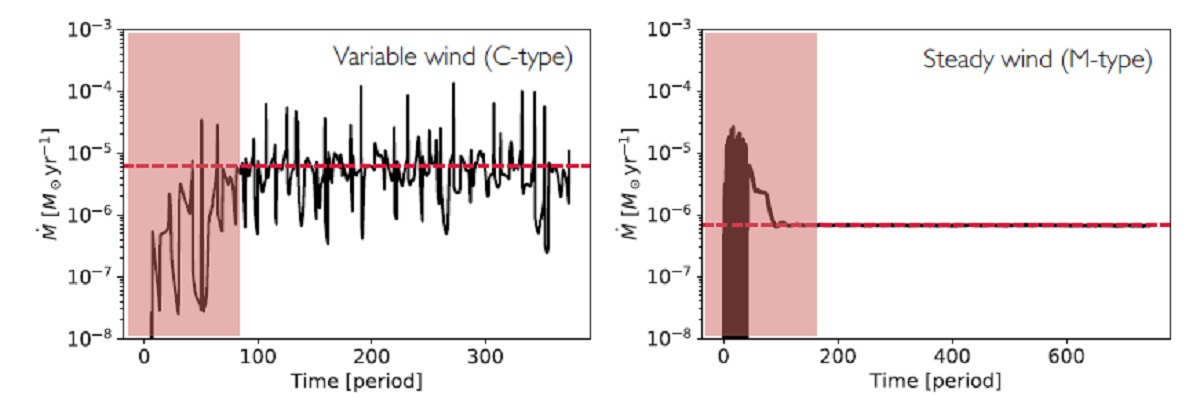
　マスロスの振動　

　図４には数百変光周期で平均したマスロス変化の例を示す。左は炭素星、右はM-型星である。炭素星の（数百周期平均）マスロスの時間変化が平均＝赤線の周りに激しく揺れるのに対し、M-型星のマスロスは極めて安定している。

　X Shooter、干渉計による検証　

　Lancon は IAU Symp 343 のトーク "O-rich LPVs in the X-shooter Spectral Library" でDARWIN モデルSED と観測スペクトルの比較を行った。また干渉計との比較も M-AGB を Sacuto et al 2013, Bladh et al 2013 が、 C-AGBは Sacuto et al 2011, Rau et al 2017, Wittkowski et al 2017 が行った。

図７．炭素星モデルからのスナップショット。Nowotny et al 2011 より。左上：ガス密度とダストに含まれる炭素原子の割合。左下：ガス速度と温度。右上：位相による光度変化。右下：φ=0.53 における SED. 緑線＝星SED。