| ケプラーの 34 日分データから赤色巨星の太陽型振動を検出した。測光は 30 分間隔で行われた。対象星は K-, G-型巨星で、光度はレッドクランプから巨星 枝基底部に及ぶ。振動数間隔 Δν と極大パワー振動数 νmax の間に強い相関が見つかった。S/N 比の高い低光度 νmax > 100 μHz, L ≤ 30 Lo の 50 星で太陽型振動を確認した。それらは水素 殻燃焼星で、進化計算と星形成史に貴重な情報を与える。 | 振動数をスケールして新しいエシェル法で解析して、動径および非動径振動に 対応する系列を発見した。その中には l = 3 振動も含まれる。l = 0 と l = 2 振動の小さな差を測り、ν02 - Δν プロット、いわゆる C-D 図を作成した。隣接 l = 0 の中間点と l = 1 との差は、太陽や太陽型星 での観測に反して負であった。l = 1 系列はかなり幅広でこれはミックスモード に起因すると考えられ、モデル予想と一致する。 |
|
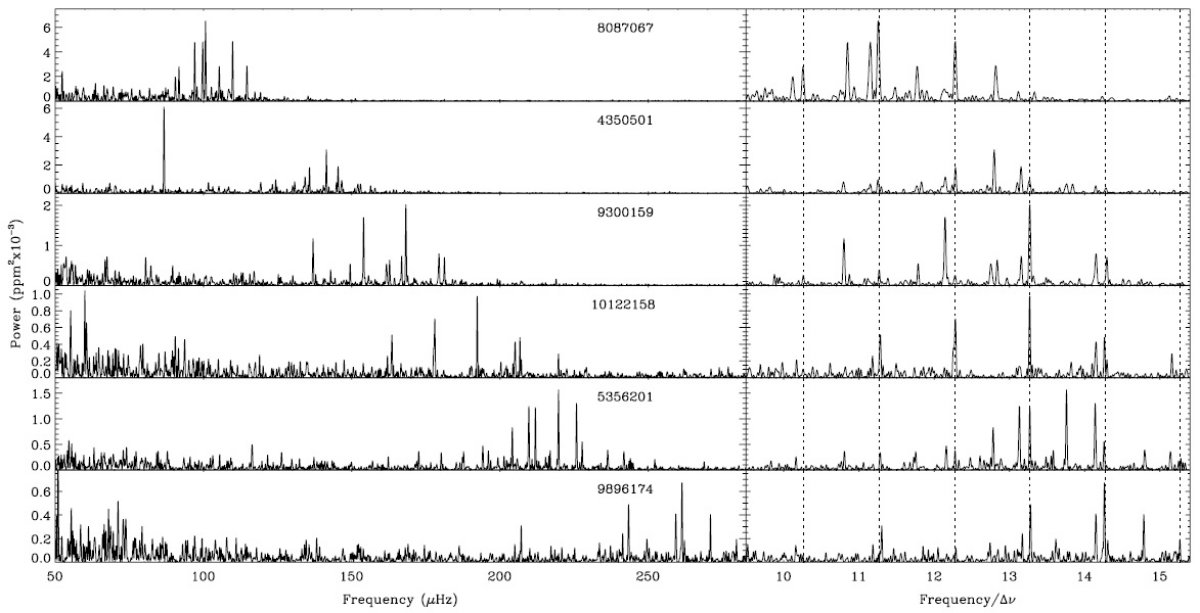
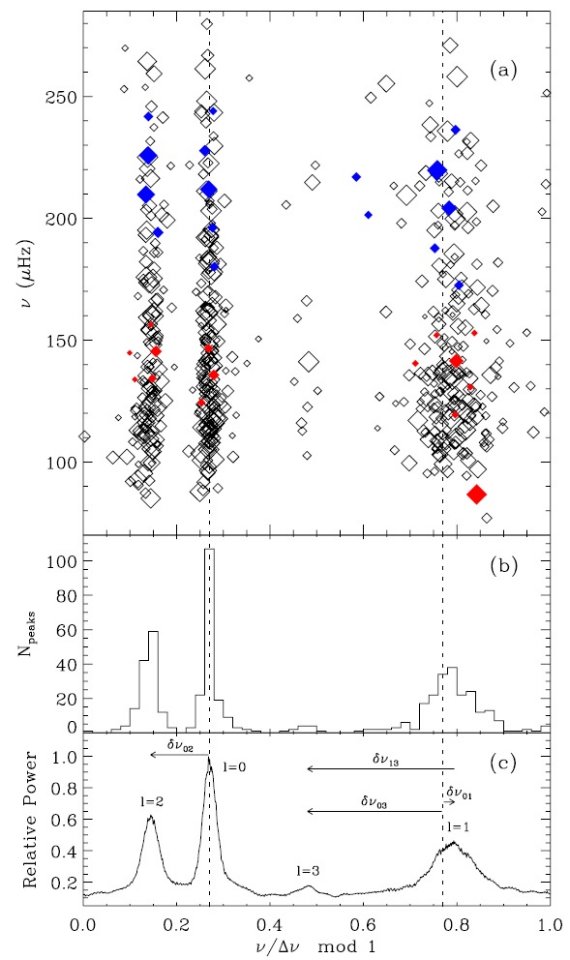
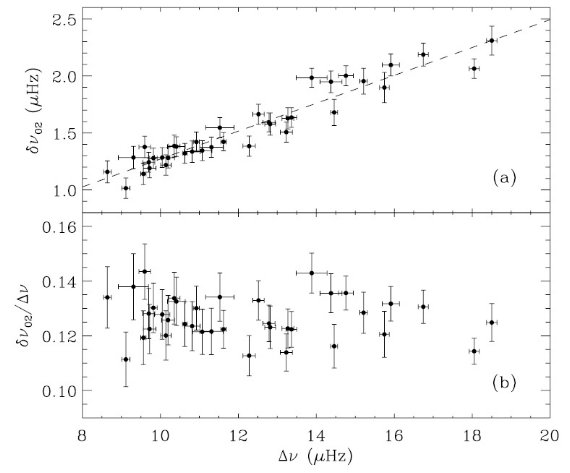
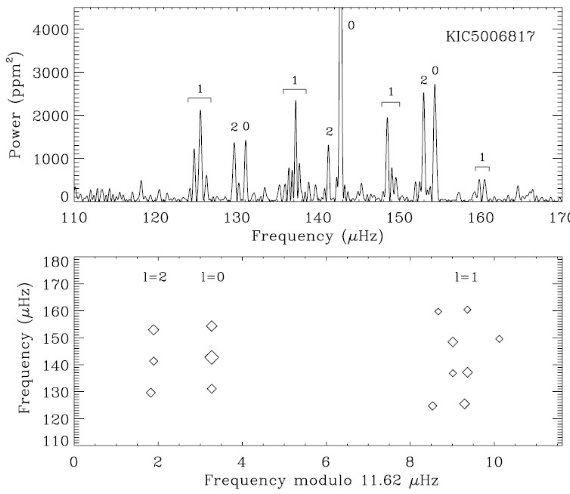
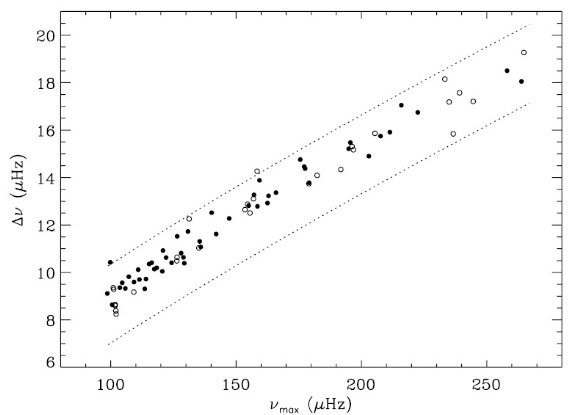
ケプラー観測 ケプラーの 29.4 分間隔 34 日間のデータを約 1500 の赤色巨星に対して 取得した。 20 % の星に 1 % 以上の変光が検出された。それらは M-型巨星 の変光でここでは解析しない。残りの星に関して変光曲線を解析し、 極大パワー振動数 νmax と大きな振動数間隔 Δν を求めた。約 1000 個の星でノイズ以上の超過パワーを認めた。約 700 星では Δν を決めることが出来た。今回は CoRot で解析が行われていない 低光度赤色巨星を扱う。 図１＝ νmax - Δν 関係 図１は νmax と Δν の関係を示す。この相関に関し ては、Hekker et al 2009, Stello et al 2009 が議論した。今回の結果は それらをより νmax の大きな赤色巨星へ広げた。 図１．78 低光度巨星の、大きい振動数間隔とパワー極大振動数関係。 黒丸＝S/N が高く、詳細解析を行った 50 星。点線＝ 80 % を含む 領域境界。 |
 |
|
図２＝パワースペクトル 詳細解析を行った 50 星中の 6 サンプルを図２に示す。図２左は 変光のパワースペクトルである。規則的に並んだピークが見える。これは 太陽型振動の特徴である。 振動モード 太陽型振動は高次の p-モード振動である。その振動数は主系列星では以下の 式で表される。 νn,l = Δν(n + l/2 + ε) - (l(l+1)Do (1) |
ここに、 n = 動径次数、l = 角次数である。Δνは音波が星を横切る
時間の逆数にほぼ等しい。Do は中心核近くでの音速勾配に鋭敏な量で、
ε は表面層に鋭敏である。
振動数間隔 ここでは３種類の振動数間隔を問題にする。 δν0, 2 は、隣り合う l =0 と l = 2 の間隔。 δν1, 3 は、隣り合う l =1 と l = 3 の間隔。 δν0, 1 は、 l = 1 の両側の l =0 の中間点からの l = 1 のずれ。 式（１）が適用できるなら、δν0, 2 = 6Do, δν1,3 = 10Do, δν0,1 = 2Do である。 |
３．２．半規格化エシェル図エシェル図の作成太陽型振動のモード振動数を解析する強力な手法がエシェル図(Grec et al. 1983) である。それは大きな振動数間隔 Δν で折り重ねる。 結果が図３a で50 星を一枚のエシェル図に重ねた。この図を作るには、まず 動径振動を同定して、各星の振動数を Δν で切り分ける。そして、 Δν を微調整して、動径モードが一直線に並ぶようにする。 半規格化エシェル図 図３は Bedding, Kjeldsen 2010 のエシェル図と大事な点で異なる。図３ では横軸だけが折り重ねられていて、縦軸には元々の振動数が使われる。 そのためにデータ点が散らばり νmax に伴う変化が見える。 このような図を半規格化エシェル図と呼ぶ。 ３．３．コラプスエシェル図とモード寿命足し合わせスペクトル図３b には図３a の点のヒストグラムを示す。分布のピークがはっきり分 かる。閾値以上のピークの数を数える代わりに、我々は別の方法を採用した。 それは半規格化折り重ねスペクトルをサンプルの５０星分足し合わせて図３c とするやり方である。 モードの寿命 図３のはっきり見える系列はモードの寿命に関する考察を可能にする。 我々の結果は赤色巨星における振動の寿命が以前懸念されていたように 短くはないことを示す。 |
 図３．(a) 低光度赤色巨星サンプル ５０個の半規格化エシェル図。シンボルの 大きさは振幅を表す。青印＝ KIC 5356201. 赤印＝ KIC 4350501. Δν は星毎に l = 0 モードが左側の縦点線上に垂直に並ぶよう調整 した。他のもう一本の縦線はキッチリ 0.5 離れていて、 l = 0 モードの中間 点を示す。 (b) 図a の点のヒストグラム。(c) Δν で折りたたみ、規格化した サンプル全星のパワースペクトル。矢印は小さな間隔 δν0,1, δν0,2, δν0,3, δν1,3 を示す。左向き矢印が正間隔を意味する。 |
|
l = 2 系列 l = 2 系列は l = 0 系列に沿って並んでいる。これは δν0,2/δν が ほぼ一定値 0.125 であることを意味する。これはすなわち星がホモロガスと 看做せることを示している。我々は 38 星に対し、 δν0,2 を決定した。図４a はその結果を所謂 C-D 図として 示したものである。図の破線は直線フィットで、 δν0,2 = (0.122 ±0.006)δν + (0.05 ±0.08)μHz (2) 直線の周りの散らばりは星質量の散らばりを表すと考えられる。それは図４b の ように、二つの間隔の比として表示するとはっきりする。 l = 1 と l =0 の位置関係 図３の点線は l = 0 モードの中間点を示す。興味深いことに l = 1 系列は このラインの少し右側に位置する。これは δν0,1 が負 であり、太陽をはじめとする多くの主系列星と逆である。またそれは式１が 厳密には成り立たないことを示す。 |
 図４．(a) 所謂 C-D 図。サンプル中 38 星の δν0, 2 対 Δν を示す。破線は直線フィット。(b) δν0, 2 /Δν 対 Δν プロット。 |
|
l = 1 系列の交差回避 図３に置ける l = 1 系列は他よりも幅広である。これはミックスモードが 存在し、その交差回避により振動数がずれるためと解釈できる。ミックスモード は進化した星で外層部が p-モード、核が g-モード的な振動特性を有する結果 生じる。典型的な例は図３a の青印＝ KIC 5356201 である。その l = 0, 2 モードは各自の系列に近く沿っているが、 l = 1 の散らばりは大きい。赤印 ＝ KIC 4350501 はもっと極端で強いピークを 87 μHz に示す。このピーク が l = 1 系列に近いことはそれがミックスモードであることを示唆する。 存在を示唆している。類似の減少は F5 超巨星のプロキオンの視線速度でも見 られる。 モデル予測 Dupret et al 2009 は様々な赤色巨星枝星に対し、太陽型振動のモデル振幅 を議論した。彼らのモデルでは、赤色巨星の大部分が νmax < 80 μHz の規則的な振動数パターンを持つ。 低光度巨星で複雑化 しかし、低光度巨星では もっと複雑な構造が予測された。それらの星の核では輻射ダンピングが弱く、 p-モードと g-モードの相互作用が強いからである。これは l = 1 モードで 特にそうであり、今後の観測が重要である。 |
 図５．KIC 5006817 のパワースペクトルとエシェル図。同じ次数内に複数の l = 1 ピークが存在する。パワースペクトルの最高点はプロット限界外に ある。 |
|
検出 l = 0, 1, 2 系列以外に図３には l = 3 系列が見える。l = 3 は振幅が小さ いので検出は困難である。これまでに測光検出は CoRoT による G0 主系列星 HD 49385 があるだけである。図３a, b を見ると、l = 3 系列にあるピークは 12 ある。図３c にはよりはっきりと l = 3 系列がわかる。 |
確認 どうやって l = 3 と確認するか？便利なのは、 δν1,3 から l = 1 に相対的に l = 3 を測ることである。δν0,2 /δν0,3 = 2.0 が予想されるのに対し、観測値は 2.2 で 満足すべき結果であった。 |
| 今回ケプラー３４日間のデータから赤色巨星の太陽型振動研究が大変実り豊か である展望が得られた。今後データが増すにつれ、赤色巨星枝進化経路全体に かけての研究が可能となるであろう。 |