主な結果は簡単な標準モデルが、5領域の星計数とカラー分布を全て十分によく
フィットすることである。個別には、
(1)不確定さ
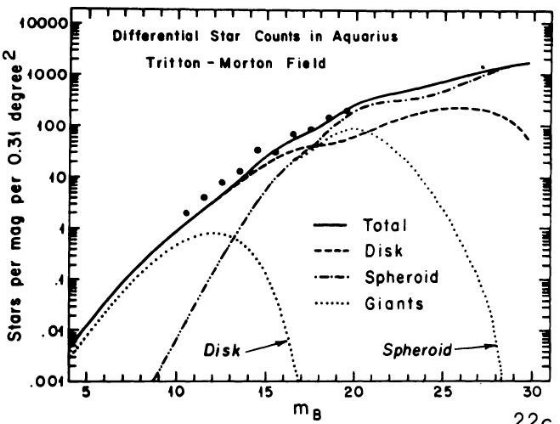
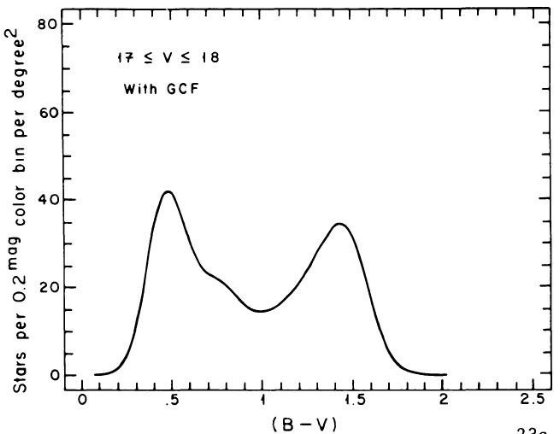
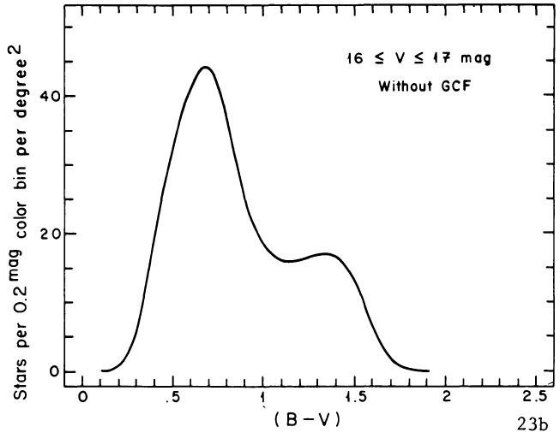
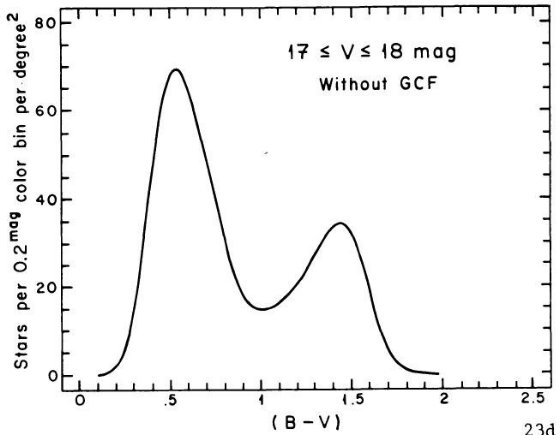
図3や 2.c 節で議論したように、使いなれた B, V バンドで比較的明るい等級
を扱ってさえかなりの不定性が伴う。それは、汎用性の低いバンドではさらに大きい
だろう。我々はモデルパラメターでカラーシフト 0.2 等、規格化で 25 % までを
許容することにした。現在のデータを考えて、全部のパラメターを動かして全てに
合う解を探す事はしなかった。各ケース毎に計算結果と観測データを示したから読者
自ら我々が設定した不確実度の範囲が適当かどうかを判断してほしい。
同じ領域の同じ等級帯を複数のグループが独立に観測、解析することが極めて
望ましい。
(2)円盤スケール高とスケール長
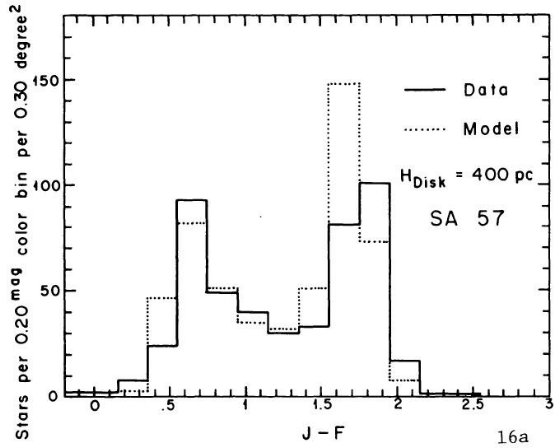
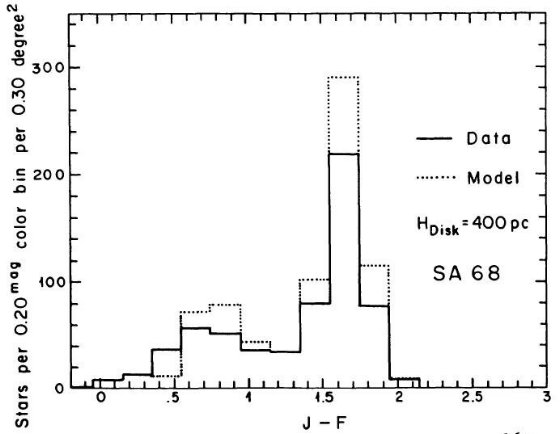
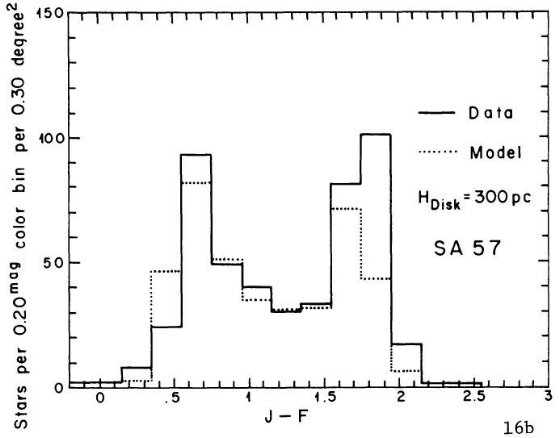
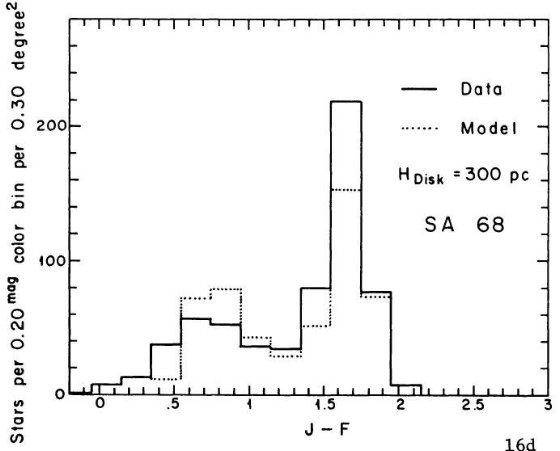
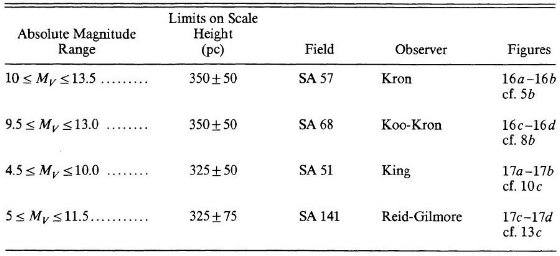
円盤矮星のスケール高は SA 57, SA 68, SA 51, SGP の観測から決まった。
Wielen の円盤光度関数がどの領域でも成立すると仮定して、我々は全ての領域に
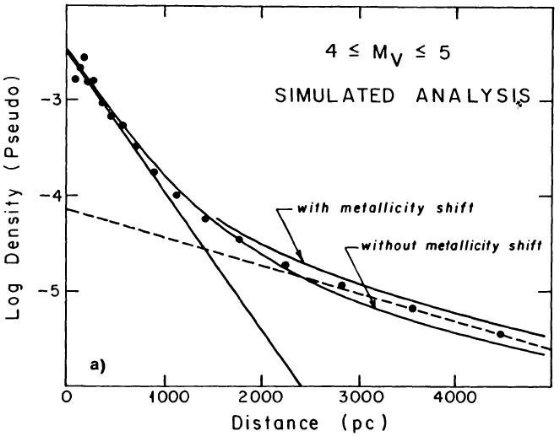
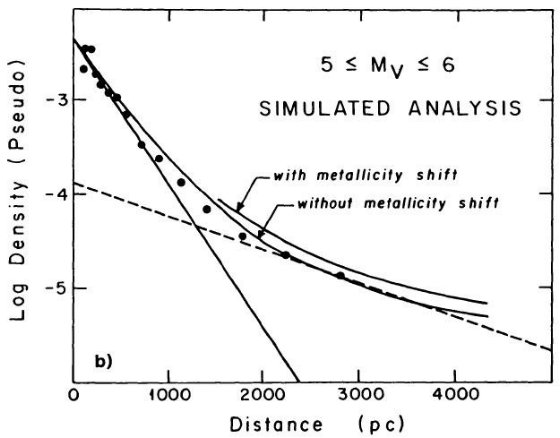
適合する解として 5 ≤ Mv ≤ 13 に対し 350±50 pc を得た。同じ
データから、 5 ≤ Mv ≤ 13 での数密度は太陽近傍の密度と ±15 %
の精度で等しい。
意味が判らない。視線に沿って密度一定?
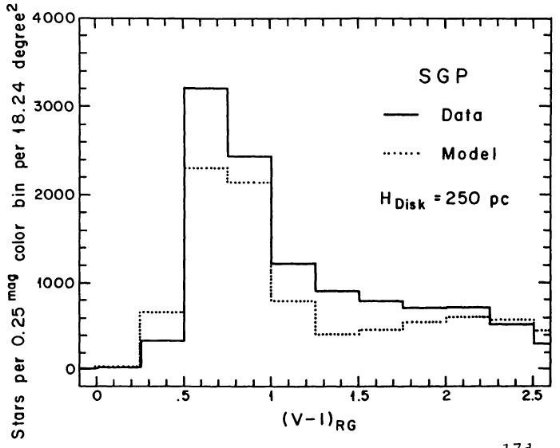
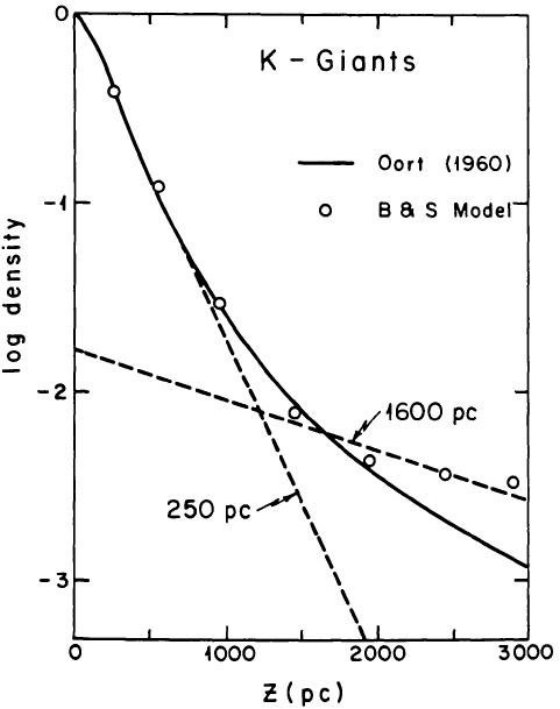
円盤巨星のスケール高は決めにくい。McLaughlin 1983 のデータを使い、巨星
スケール高を 250 ±100 pc と決めた。円盤スケール長は 2.5 kpc 以上である。
(3)光度関数に窪みがある
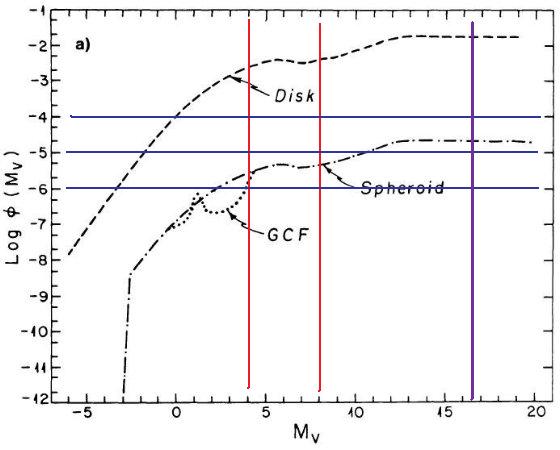
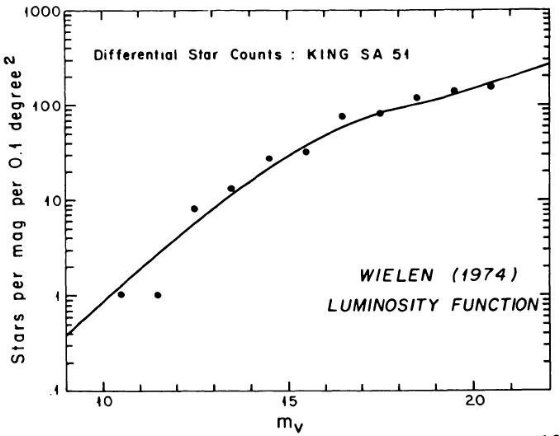
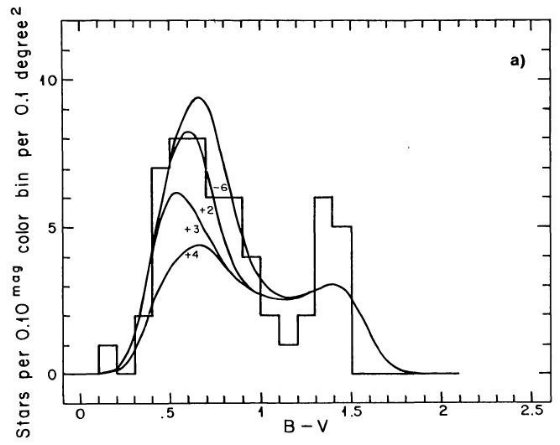
Wielen 1974 と Upgren, Armandroff 1981 は近傍星の光度関数には Mv = 7, すなわち
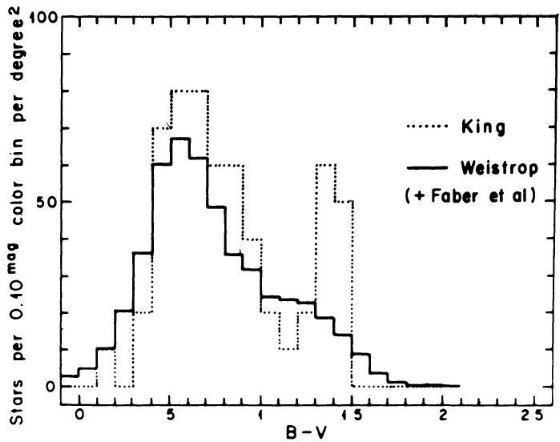
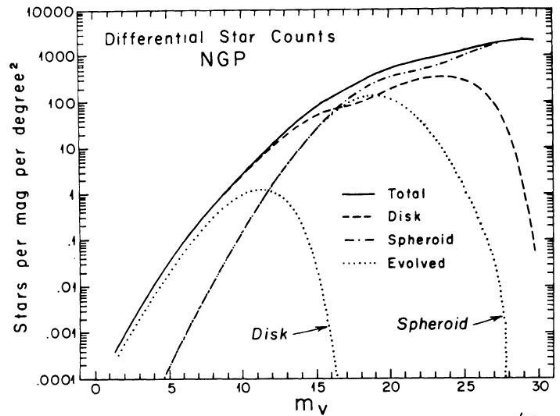
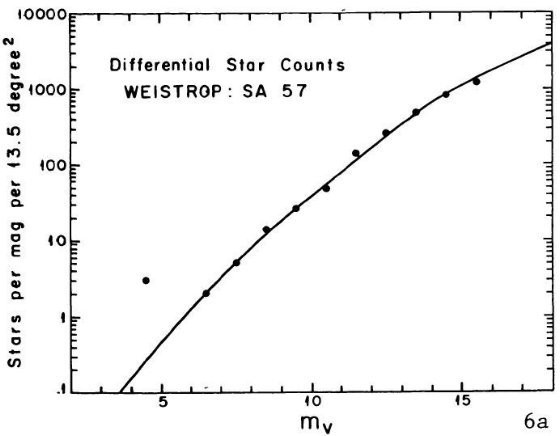
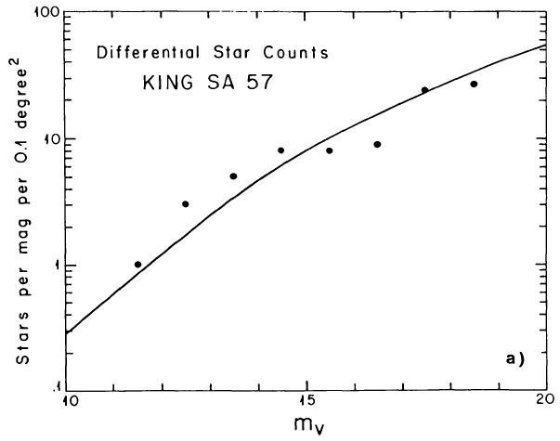
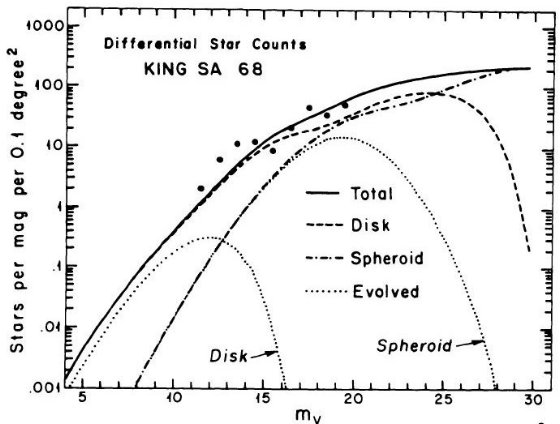
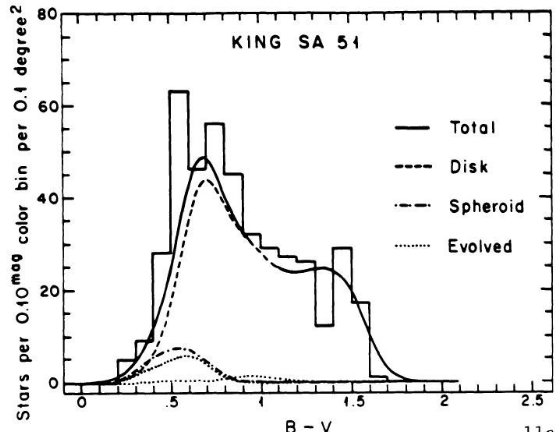
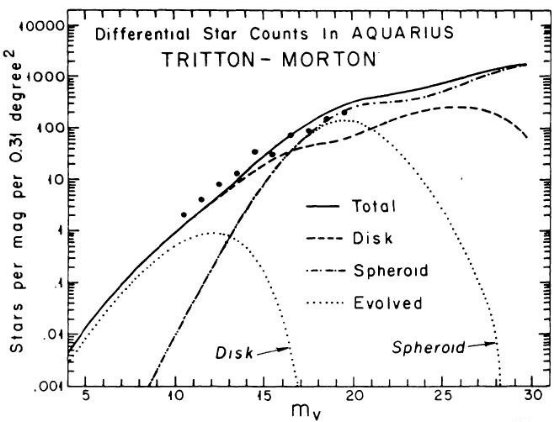
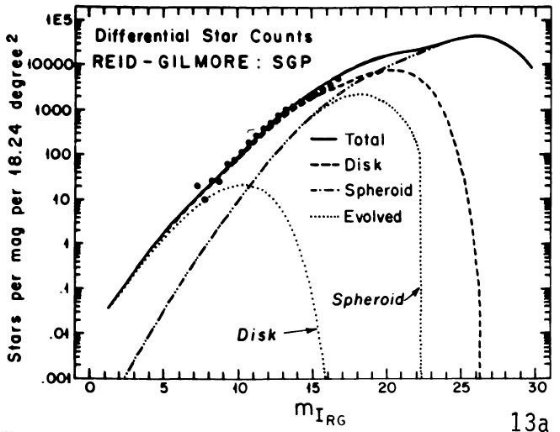
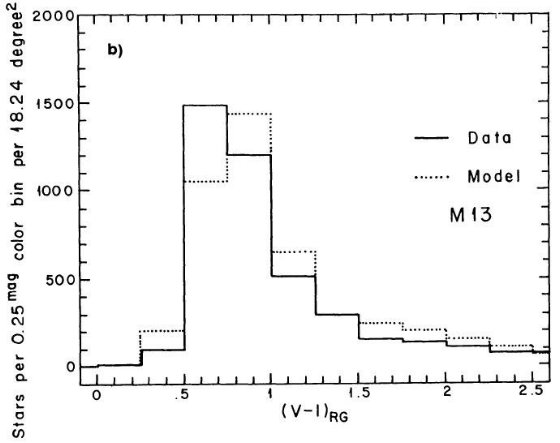
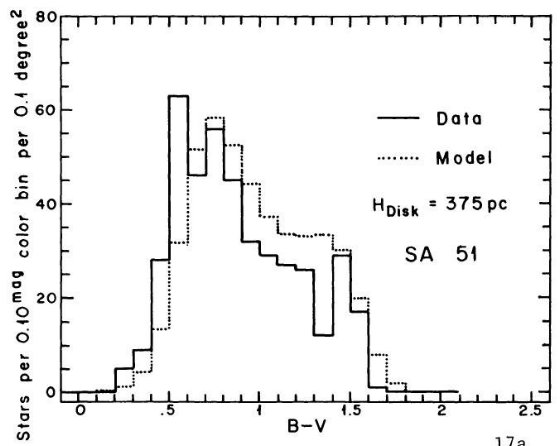
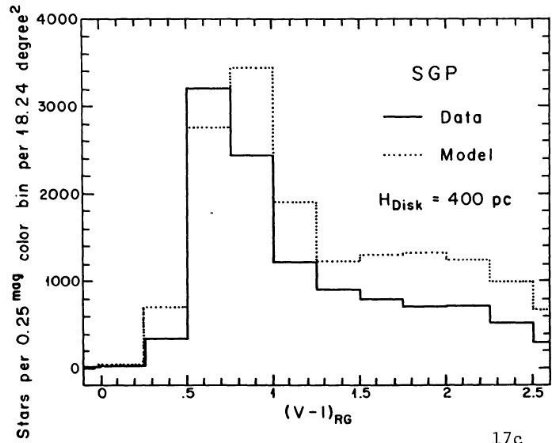
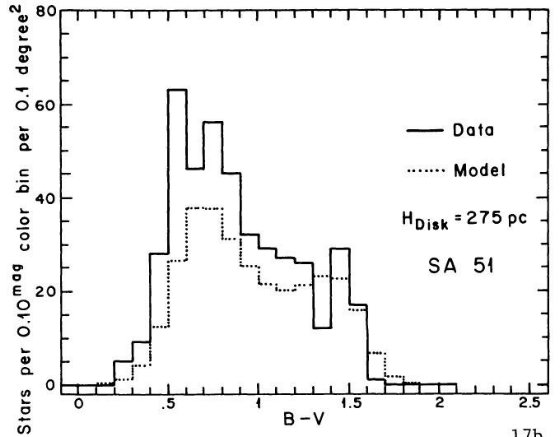
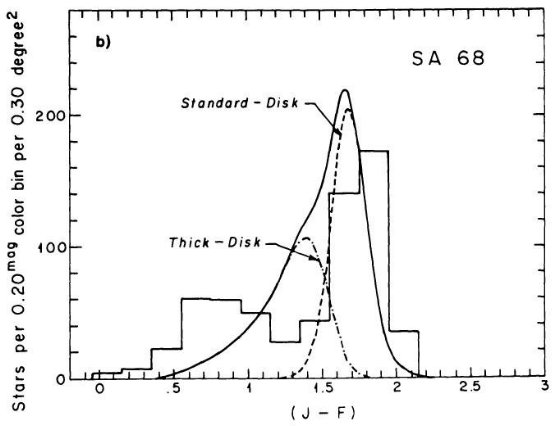
B - V = 1 付近に窪みが存在することを示した。図 1a を見よ。SA 51 領域のより
遠方の星に対し King が行った星計数とカラー分布にも窪みの証拠が見つかった。その
結果は図10に載っており、第5章で論じられている。
(4)楕円体の軸比
銀河中心から 10 kpc の所での楕円体軸比は、太陽から銀河中心方向に垂直
な面での星計数データを使って決められる。面内の3領域データがあれば、
我々は楕円体の規格化と軸比の二つを決められる。
| |
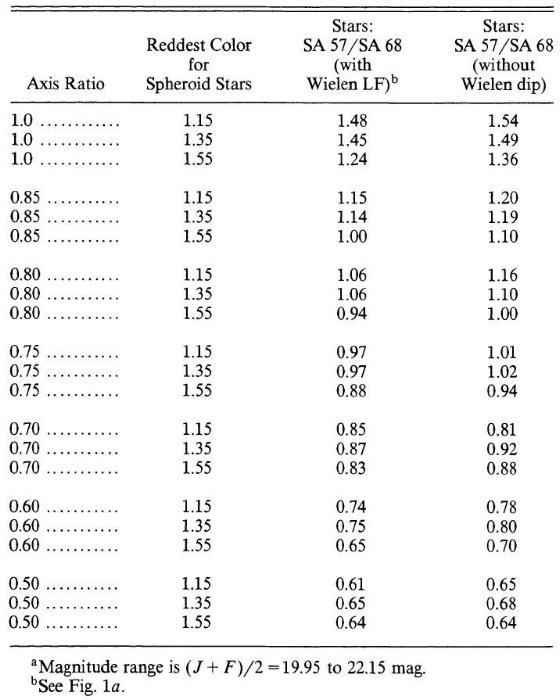
我々は2領域 SA 57 と SA 68 を使って軸比を求めた。我々の結論は b/a = 0.80
-0.05+0.20 である。この結果はもっと近距離で
Oort, Plaut 1975, Fall 1981 により得られた値とよく一致する。また、球状星団
システムに対する Frenk, White 1981 の値とも合う。軸比が距離により変化する
証拠はない。
楕円体の規格化は 2d 節で与えられた。それは Wielen 1974 が決めた近傍星
数密度の 1/500 である。
(5)メタル量勾配
データにはメタル量勾配を示唆する証拠がある。楕円体成分への寄与が最大になる
距離が Bahcall 1983 に述べてある。それによると、SA 57 (10.5 kpc),
SA 68 (11.5 kpc), SA 51 (13.5 kpc), 水がめ座 (7.7 kpc), SGP (10.5 kpc)
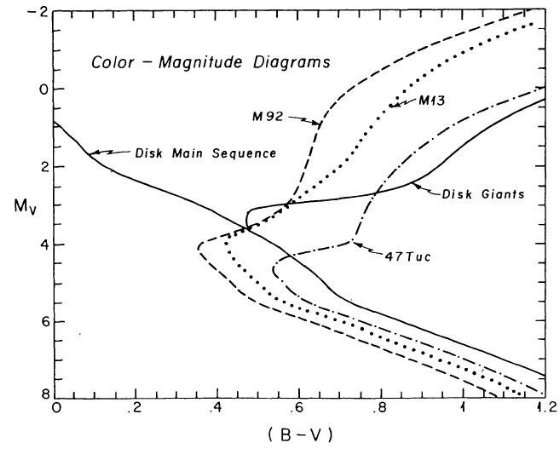
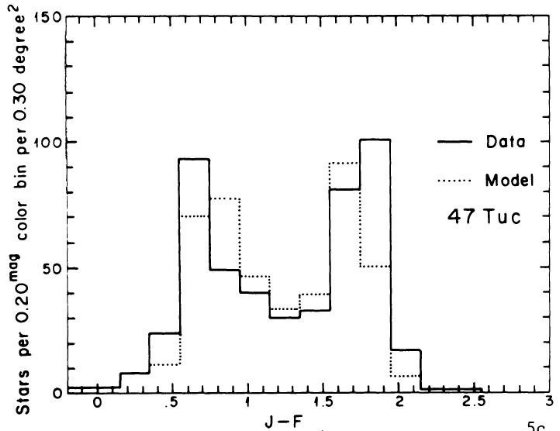
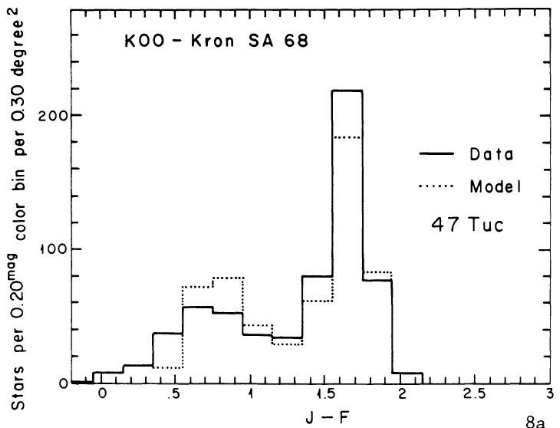
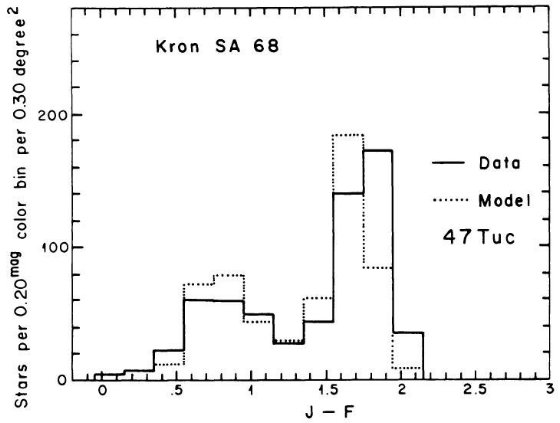
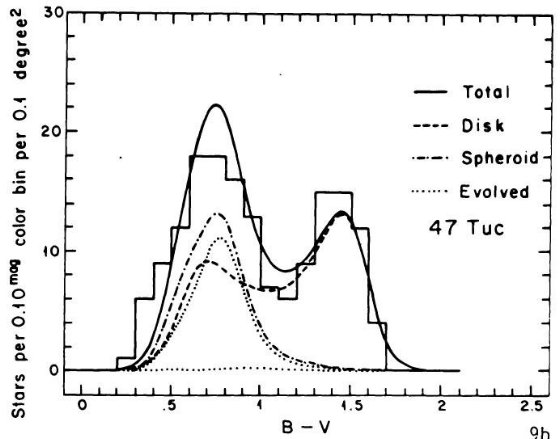
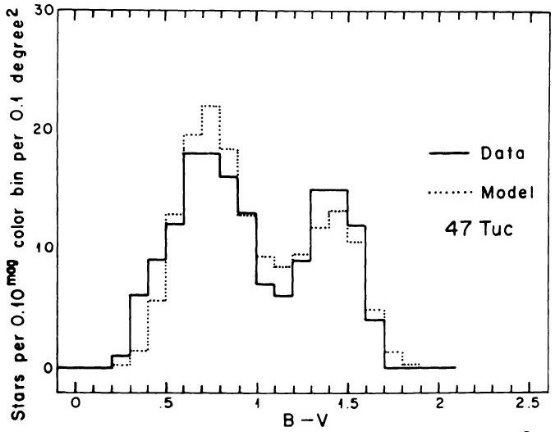
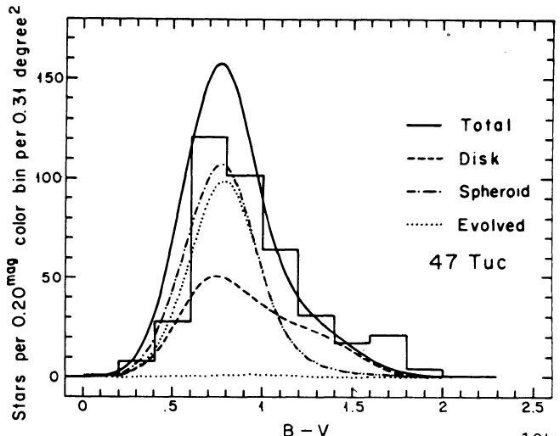
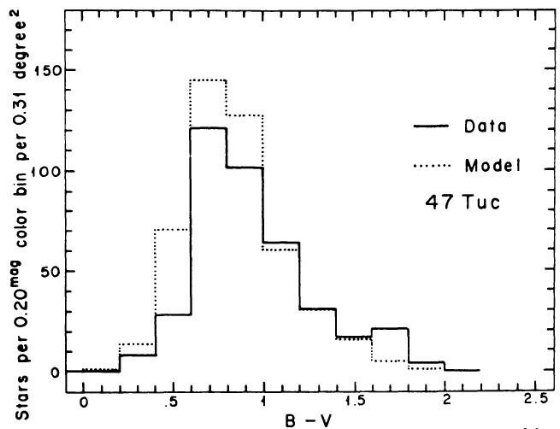
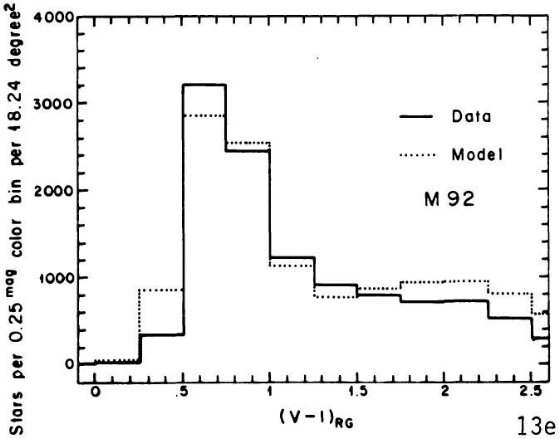
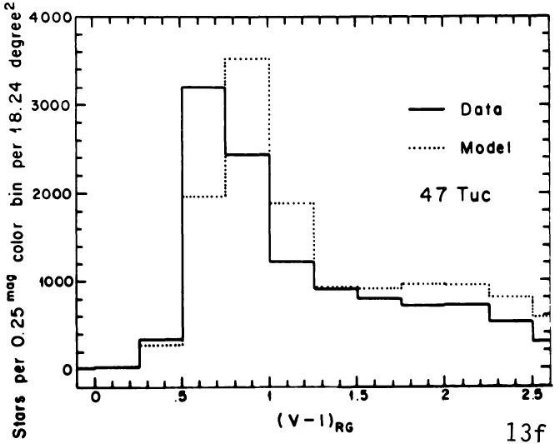
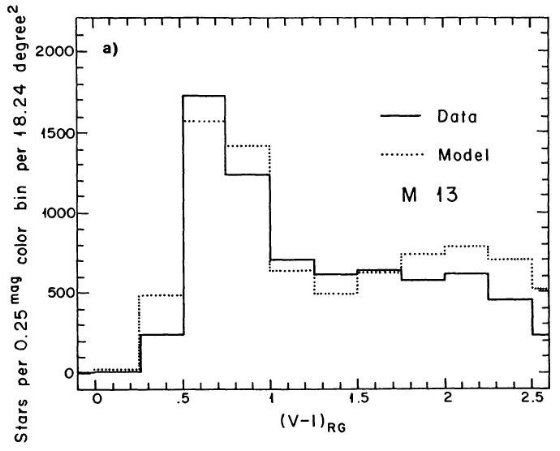
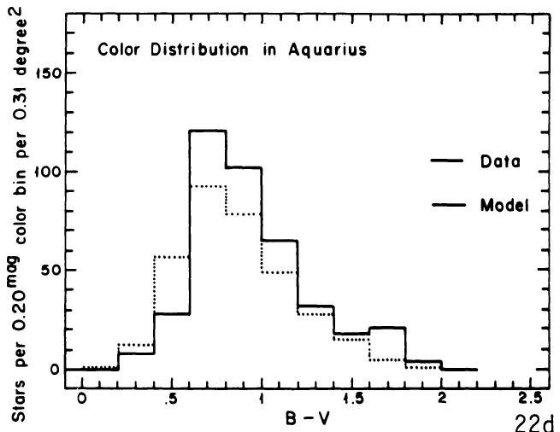
である。銀河中心距離が最小となる水がめ座では 47 Tuc 色等級図が最良フィット
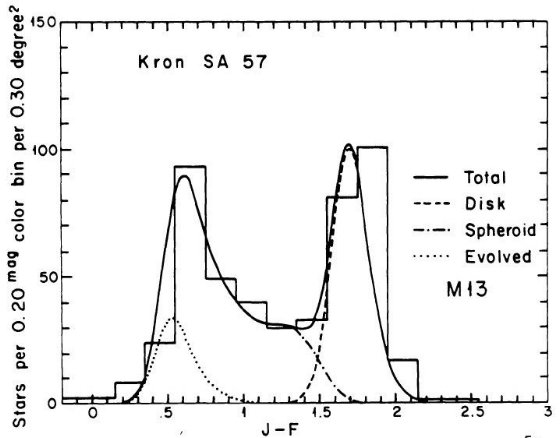
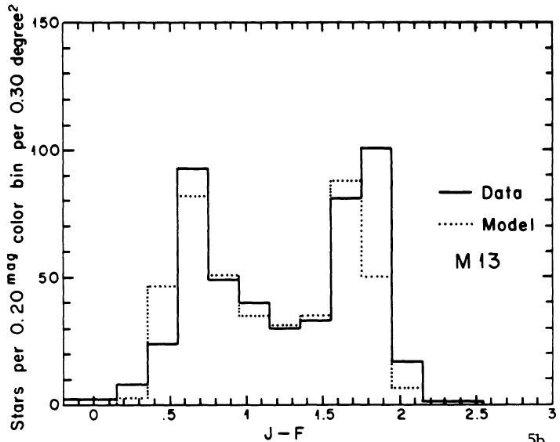
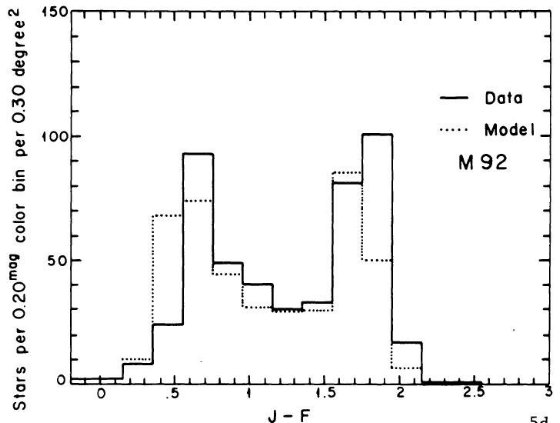
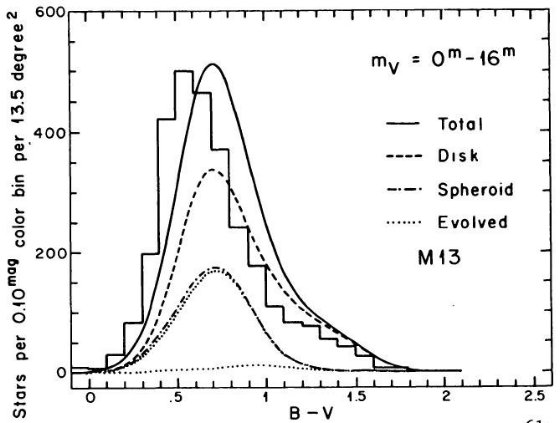
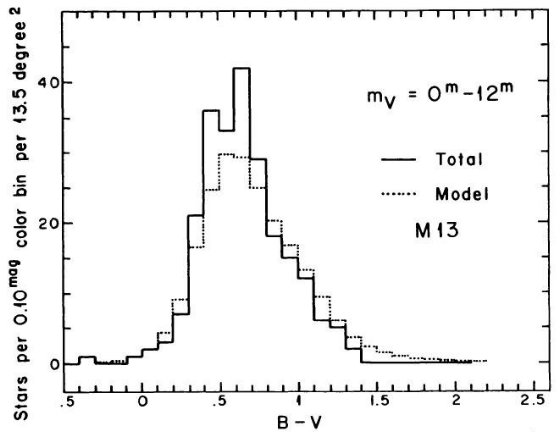
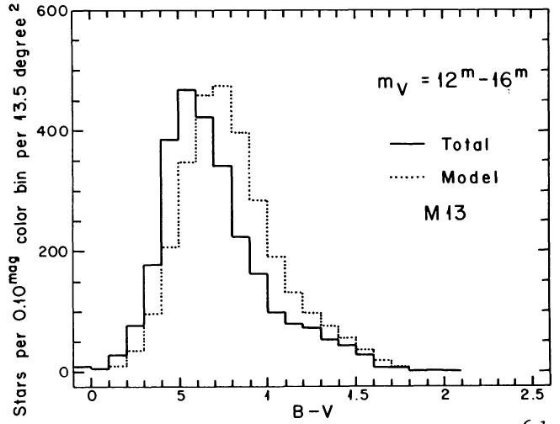
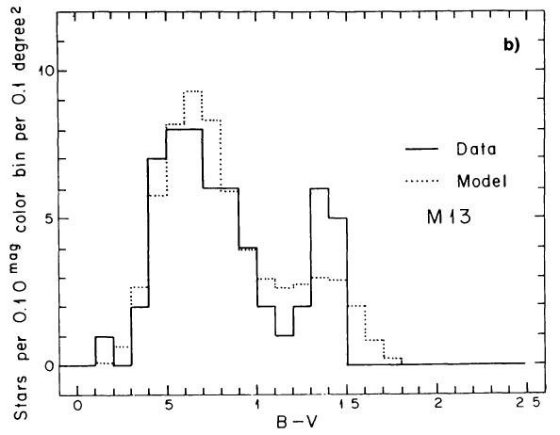
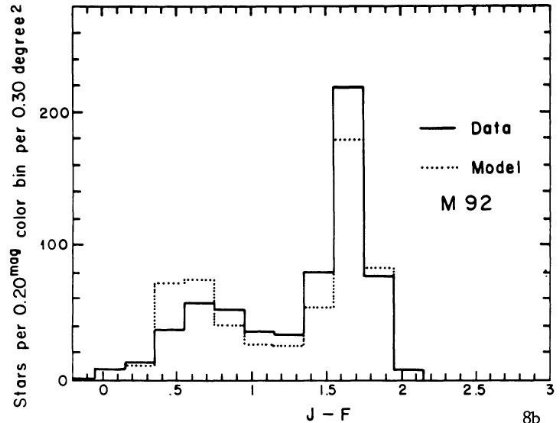
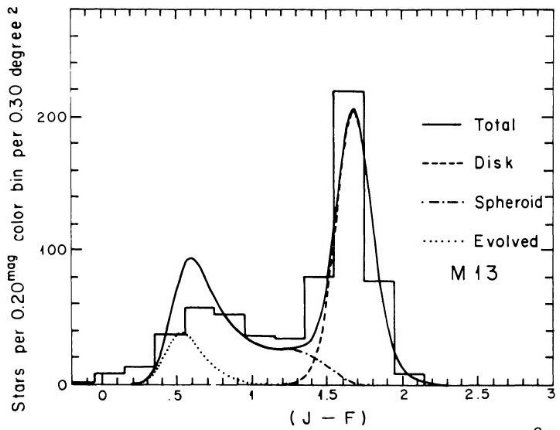
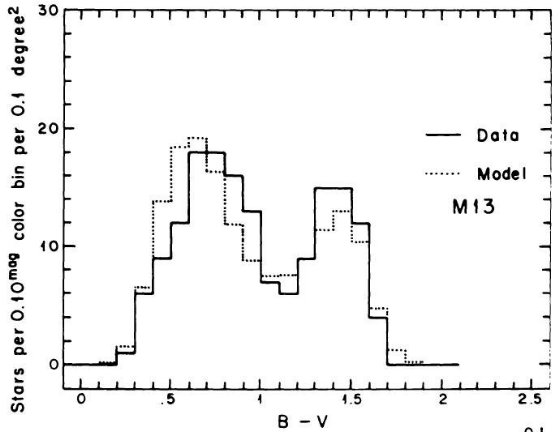
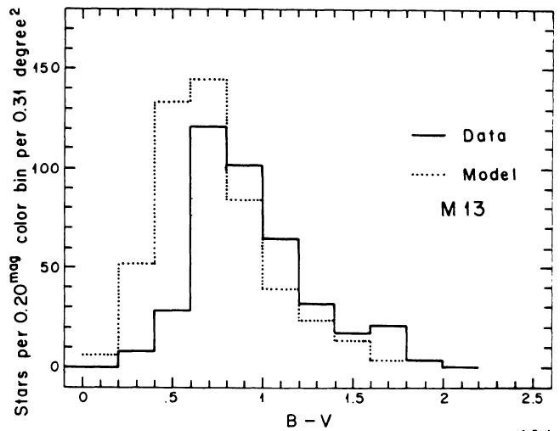
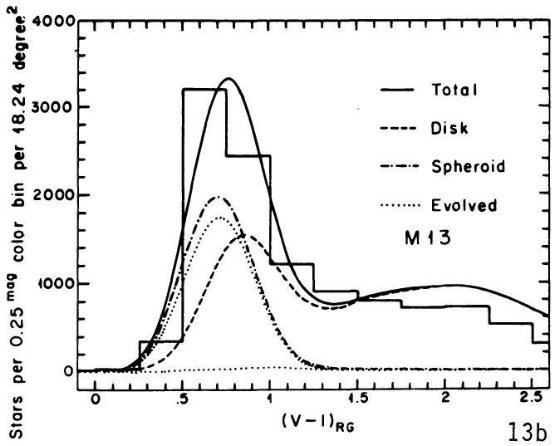
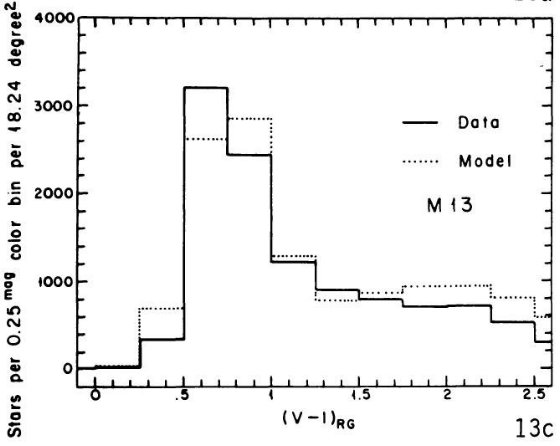
を与えた。中間銀河中心距離の SA 57 では M 13 がよかった。これは他の銀河で
見られる銀河中心距離と共にメタル量が低下する現象に合致する。
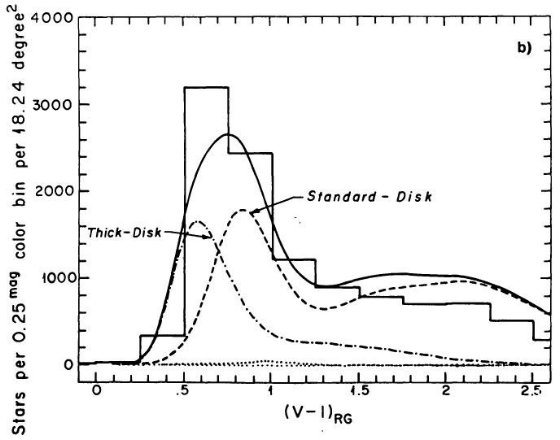
(6)楕円体巨星の存在
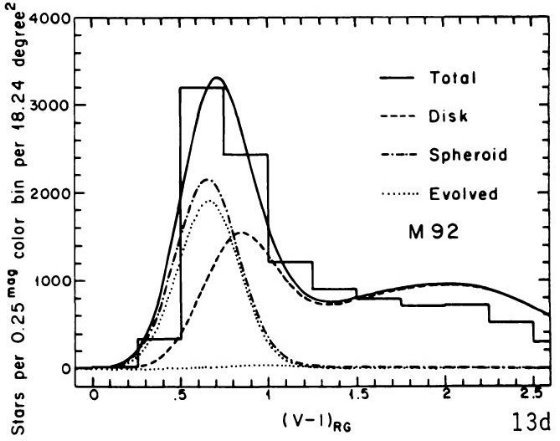
中間等級 V < 18 の楕円体星の殆どは巨星か準巨星である。これは球状星団
色等級図を使用したための結果である。カラー分布の計算は球状星団の色等級図
がくねくねしているためにとても厄介である。この曲線はスプラインで近似して
カラー分布を出すのに使うべきである。この作業を飛ばすと正しい解が得られない。
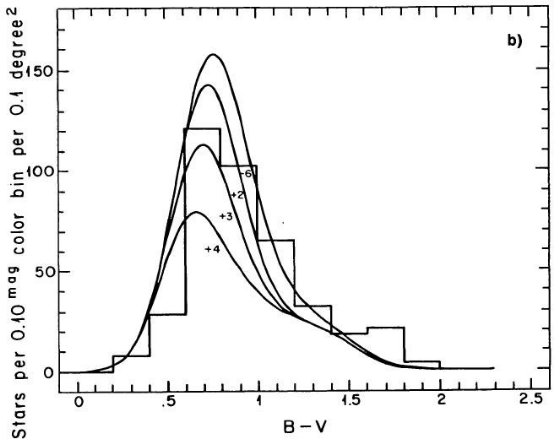
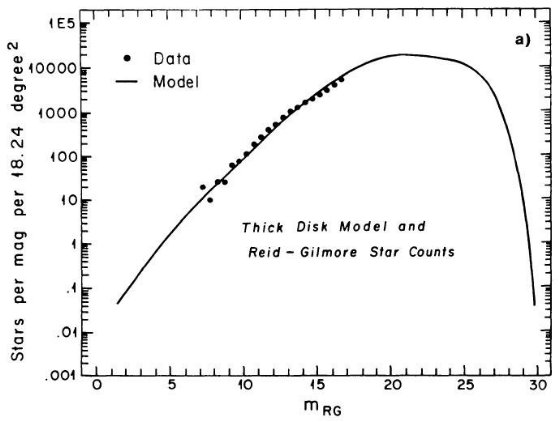
Ratnatunga 1982 の分光サーベイは多数の楕円体巨星を確認した。Gilmore, Reid 1983
が仮定した、Mv = +4 で光度関数が急落する現象の証拠は見出せなかった。
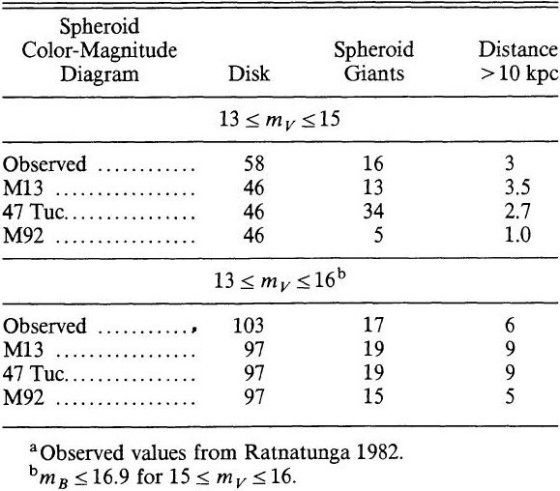
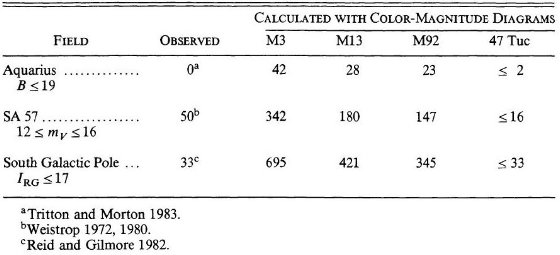
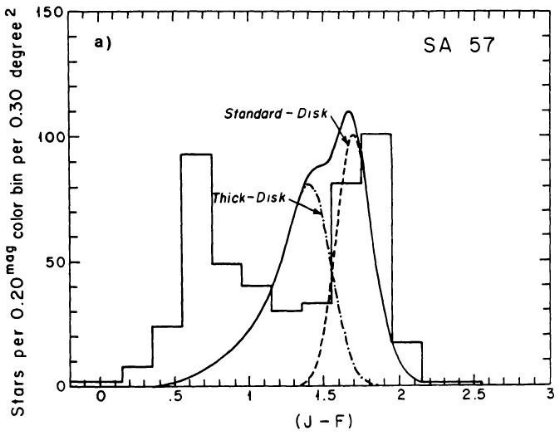
(7)楕円体星には水平枝青端がない
SA 57, 水がめ座、SGP の観測から、楕円体フィールド星には水平枝青端の星が欠けて
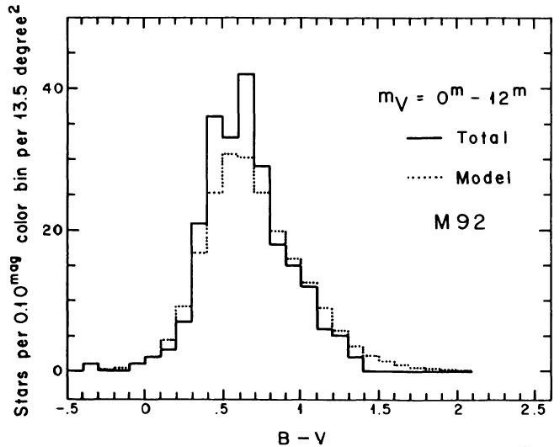
いることが判った。もしも、楕円体フィールド星が M3, M13, M92 と似た水平枝を有して
いるならば、 B - V < 0.2 の青い星が観測されているよりは少なくとも10倍は
見つかるはずである。この結果は表5にまとめてある。観測は楕円体フィールド星が
47 Tuc 的な色等級図を持つという仮説に合致する。
|