The Distribution of Stars to V=16th Magnitude near the North Galactic Pole
Normalization, Clustering Properties, and Counts in Various Bands


Bahcall, J.N., Soneira, R.M.
1981 ApJ 246, 122 - 135



　アブストラクト

　北銀極近くでの V = 16 より明るい星の分布を論じる。最も重要なデータは Weistrop のものである。全てのデータは、もし巨星を矮星と別に扱えば、我々の 標準銀河モデルの予想と合致する。

　色々な測光バンド間の変換が与えられる。将来現れるかも知れないバンドに 対しても適用できるような材料を与えた。

　スターカウントはそこに出てきたバンドに対し、１６等まで予言した。

　２点相関関数を用いて星のクラスタリングを調べた。15 % の星は連星か３重星 に属している。

　1.イントロ　



明るい星は渦状腕と星形成領域のの位置を示す　

　非常に明るい星と非常に暗い星の分布は銀河構造に重要な情報をもたらすと考え られてきた。明るい星は渦状腕と星形成領域のの位置を示す。暗い星は銀河系の 形と質量の標しになる。

 中程度 9 ≤ V ≤ 16 明るさの星が銀河モデル に大きな拘束　

　この論文ではしかし、中程度 9 ≤ V ≤ 16 明るさの星が銀河モデル に大きな拘束を付けることを示す。この分野では Lindsay, Bok 1957, Bok, Basinski 1964 の先駆的研究がある。また、スターカウントの規格化、つまりある等級 より明るい星が１平方度あたり幾つあるか、も重要な問題の一つだ。

　恒星の中間等級領域で、現在あるデータは Weistrop 1972, 1980 の NGP 方向の ものである。したがって、B&S モデルを用いて銀極方向の星計数の観測結果を 調べ、他の方向での星計数を予言する。

　第２章では規格値を論じる　

　第２章では Weistrop カタログを古い Seares et al 1925 と比較する。我々の 得た規格値は Allen 1963, 1973 の値より 40 % 低いがその理由を考察する。さらに 我々のモデルの規格値が Weistrop 1980, Seared et al 1925 の結果と一致するこ とを示す。

第３章では U,B,J,V,F,R,I,g,r バンドへの変換　

　第３章では U,B,J,V,F,R,I,g,r バンドへの変換を調べる。変換に必要なパラメター を論じる。

第４章は２点相関関数を用いた解析　

　第４章では Weistrop データに２点相関関数と第１及び第２近傍星距離を用いた 解析を行う。V ≤ 12 で 2' 以内予想外に強い相関が得られた。この結果は 0.1 pc に対応する。

　２．明るい星の密度　

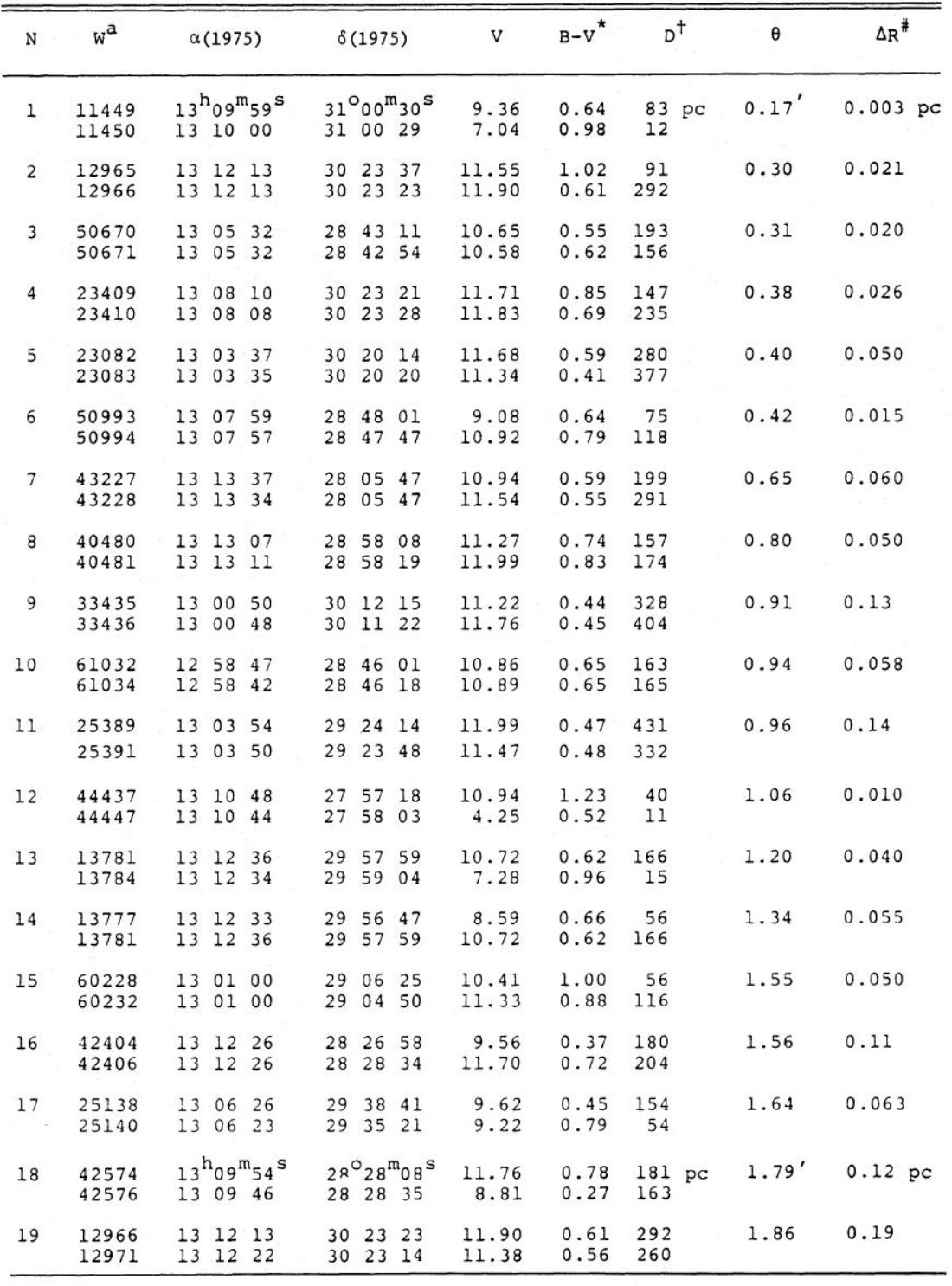
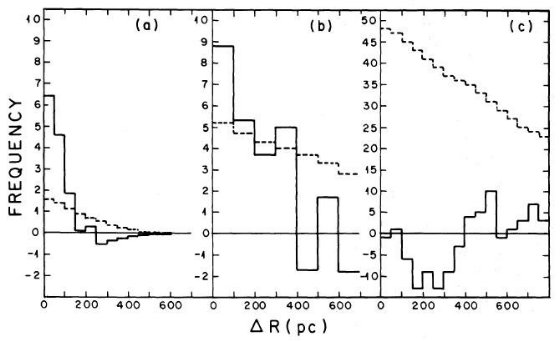
　２．a. 最良データ　

Weistrop 1980 の最新データを解析する　

　 Bahcall,Soneira 1980b で使用したデータは Seares et al 1925 の 4 - 18 等データだった。この論文では Weistrop 1980 の最新データを解析する。そのカタログは 13.5 deg2 内の V = 16 mag より明るい星が 2989 個載っている。エラーは ± 0.1 等 である。

色々なデータをまとめると　

　図１には色々な星計数をまとめてプロットした。実線は 　 Bahcall,Soneira 1980b で提案したモデルの予測値である。

　２．b. Allen の推奨する星計数　

Allen の誤り　

　Allen A.Q. の星計数は図１に比べると 40 % 以上大きい。Allen のデータには ３つの系統誤差が含まれている。それらは、

（１）Allen のデータ整約の誤り
（２）写真等級から実視等級への変換の誤り
（３）等級スケールのエラー
である。



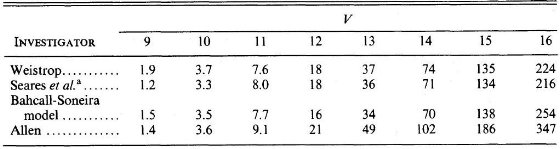
表１．極方向の累積星計数の比較

　２．c. 理論モデル　

巨星の寄与分を主系列星から分ける　

　B&S モデルで星計数を出す際に、巨星の寄与分を主系列星から分けて考えることに する。巨星の寄与は 11 等で全体の 20 % に達するが、 13 等では 3 % に下がる。
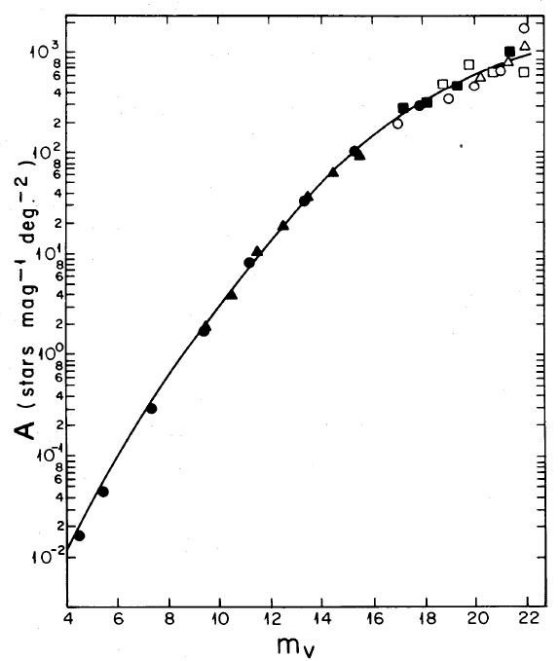
図１．銀極方向の星計数(deg-2) 実線＝ B&S モデルの予測。 巨星の寄与も含む。 黒丸＝ Seares et al 1925 データを V 等級に変換。黒三角＝Weistrop 1972, 1980。 黒四角＝Brown 1979, 白三角＝ Kron 1978, 白丸＝ Tyson,Jarvis 1979、 白四角＝Peterson et al 1979

円盤での主系列星の割合　

　円盤での主系列星の割合 f を次の式で与える。
f = { 0.44 exp[0.00015(M+8)3.5],　　　 (M < 3.7)
1　　　　　　　　　　　　　　　 　　　(M > 3.7)


巨星のスケール高は 250 pc とする。

　３．色々なバンドでの星計数　

　４．統計　

　４．1. 二点相関関数　

定義　

　銀河のクラスタリングの解析に用いられる統計手法を、恒星見かけ位置 に適用してみる。図２が星の位置である。
　角度 θ 離れた微小立体角 dΩ1 と dΩ2 に夫々星が見つかる確率 dP を次のように表わす：
　　　　　dP = n2(m0)[1 + ω(θ)] dΩ1 dΩ2　　　　　　　　(4)

ここに、 ω(θ) は角度相関関数、n(m0)は m0 より明るい星の表面密度である。
　すると、見かけ上の近接星の組の数 F(θ) は

　　　　　F(θ) = (1/2)N2(m0)[1 + ω(θ)] δΩ(θ)/Ω　　　　　(5)

δΩ(θ) = 2π ( 1 - 4 θ ) θ δθ, 　　　　(5)
π L




図２ a. 銀極方向 12 等より明るい星の位置。 		ここに、N(m0) は m0 より明るい星数、Ω は領域、 δΩ(θ) はある点の周り半径 θ±δθ のリングの Ω 内での立体角である。ファクター (4/πL) は 四角いサーベイの境界の補正である。

極方向の相関値　

　極方向の相関値を観測位置から計算すると下のようになる。ω の値は mo = 12 では θ < 2', mo = 16, θ < 0'.4 では有意にゼロと異なる。しかし、12 < mo < 16 で、θ < 2'.0 の超過ペア数の期待値は 1 - 1.5 組 deg-2 である。

mo = 12
θ 0 - 1' 1' - 2' > 2'
ω 4.7 0.4 0
　
mo = 16
θ 0 - 0.'2 0.'2 - 0'.4 > 0'.4
ω 0.45 0.35 0




図２ b. 銀極方向 15 等より明るい星の位置。

　　

　４．２. 最近接星分布　

最近接星までの角距離分布:ランダムな場合　

　最近接星までの角距離がどう分布しているかは短距離クラスタリングを 調べる強力な方法である。図３は mo = 12 と mo = 16 に 対する Weistrop データの最近接距離分布である。ランダムなポアソン分布に対する 距離分布は以下の式で表わされる：

　　　　　F(θ) = 2π n2(mo) Ω θ exp( -π n θ2) δθ　　　　　　(6)

観測データからは？　

　mo = 12 の時、θ = 1'.0 ではランダム予想の 5.5 倍のペアが、 θ = 2'.0 では 2.5 倍のペアが見つかった。 mo = 16 の時、θ = 0'.4 ではランダム予想の 1.5 倍のペアが 見つかった。



図３a. mo = 12 に対する Weistrop データの最近接距離分布 		密度の揺らぎ　

　ペアの超過が局所的な密度の揺らぎによる可能性を計算した結果、その確率は 無視できるほど小さかった。

ペアの特徴　

　θ ≤ 2' のペアの主な特性は、表５に載せてある。約８組は偶然、１１組 は物理的なペアであろう。θ ≤ 1' のペアでは２組が偶然、９組が 物理的に関連がある。この論文のデータは θ ≤ 10" や ≥ 2' の領域 には感度が低い。それでも。表５から 0.1 pc 以上離れた連星は殆どないことは 判る。









図３b. mo = 16 に対する Weistrop データの最近接距離分布



表５．　mo = 12、 θ ≤ 2' のペアの主な特性

　４．３．空間分布　

測光距離　

　測光距離を使って Weistrop データのペアの空間的な近接度を調べた。そのため、 星が主系列にあるという簡単な仮説を立てる。すると、

　　　　　Mv = 1.5 + 5.4(B - V) 　　　　　　　　　　(7)

図５には空間間隔のヒストグラムを示した。この図の実線は観測分布からランダム な場合の分布を引いたものである。マイナスの値は統計的揺らぎの結果である。
図４. 距離差分布のランダム分布との比較。(a): mo = 12、 θmax = 2',
　　　(b): mo = 16、 θmax = 0'.4, (c): mo = 16、 θ = 1' - 2',

　５．まとめ　

１．巨星を加えると Weistrop 銀極データと合う　

　Weistrop 銀極データは 9 ≤ V ≤ 16 での密度規格化に有用である。 巨星を加えると 9 ≤ V ≤ 22 での星計数は B&S モデルとよく合う。 方向による揺らぎの研究にはより広い観測が望まれる。

２．多バンドへの変換を述べた　

３．ペア　

　12 等までの星の 15 % は 0.1 - 0.3 pc 以内のペアを組んでいる。