Metallicities for Old Stellar Systems from CaII Triplet Strengths in Member Giants

1.イントロ　 　 Olszewski et al 1991 は LMC の星団で CaT によるメタル量決定を試みた。 これはかなり高メタルの天体に対する仕事になった。我々は矮小銀河への応用に 興味があるため低メタルから中間メタル量の較正を行う。 　2.観測とデータ整約　 　選択　 　観測した６星団を表１に載せた。観測星は TRGB からその 2 等下までの間の 非変光星を選んだ。AGB 星は省いた。 (これで本当にAGB星が省けるかは疑問。) 観測　 　CTIO 4m 望遠鏡で 分解能 3.1 A の分光器を使い、 8180 - 8880 A の スペクトルを取った。ラインはガウシャンフィットして二つの擬等値幅の和 W8542 + W8662 を求めた。 　表３にその結果を載せた。星番号は Da Costa, Armandroff 1990 のもの である。 　視線速度もクロス相関法で求められた。 表１．観測星団のパラメター 表２．CaT 両側の連続光部分

表３．CaT 擬等値幅の観測結果

　３．較正用星団での CaT 強度　

赤色巨星の CaT 擬等値幅系列 　図１には W8542 + W8662 と MI との 関係を示す。星団毎に巨星が強い系列を成し、メタル量により系列が分離している。 一つの系列の中での MI による W8542 + W8662 の変化量は、 MI 一定で比べた時の異なるメタル量の系列間の間隔 より小さい。図２には同じようにカラー (V-I)o による W8542 + W8662 の変化を示した。 (V-I)o は温度指標として (B-V)o より 優れている。図１と同様に一つの星団赤色巨星枝星の系列と、メタル量による 系列間の分離が現れているが、系列線がカーブしている。また (V-I)o の 変化量は低メタルになると小さくなる。この様な点で、 MI の 方が (V-I)o より優れている。 　V-VHB を用いた擬等値 幅系列の表示　 　しかし、 MI を求めるには距離、赤化が必要である。図３に示す (V-VHB, W8542 + W8662) プロットは その困難から免れている。さらに良い事に 47 Tuc と NGC1851 の間隔は図１より 開いて見える。また、図１と異なり、系列線の勾配はメタル量に依らず一定である。 　　Δ(W8542 + W8662) = (-0.619±0.010) Δ(V-VHB) 図２．CaT 擬等値幅 W8542 + W8662 と (V-I)o カラーの関係。

図１．CaT 擬等値幅 W8542 + W8662 と MI の関係。 メタル量の違う星団間の分離、特に低メタルで差が出ることに注意。 図３．CaT 擬等値幅 W8542 + W8662 と 等級差 (V-VHB) の関係。

変換擬等値幅　 　変換 CaT 擬等値幅は 　　W' = (W8542 + W8662) + 0.619(V-VHB) で定義される。この量を使うと、異なる光度の星のライン強度を直接比べる事が 可能となる。我々は従ってこの量を今後使用する。変換擬等値幅とメタル量との 関係を見るために、図４には星団の [Fe/H] との関係をプロットした。 [Fe/H] が -2.2 から -1.2 までは直線関係になり、それより高メタルでは等値幅は あまり伸びない。直接の比較は困難だが、 　 Olszewski et al 1991 にも大体同じあたりで傾きの変化が見られる。 　傾きが変化する理由　 　（１）メタル量が高くなると弱いメタル線で擬連続光のレベルが低下する。 　（２）低温度星では TiO εシステムが擬連続光のレベルを低下させる。 　（３）CaT ラインの成長曲線がウイングパートになる。 　（４）[Ca/Fe] 効果 特に（４）は重要である。Lambert 1987 により、少なくともフィールド星では 太陽メタル星（[Fe/H]=0）で [Ca/Fe]=0 なのが、低メタル星になると [Ca/Fe]=0.3 まで上がる事が知られている。変化が起きるのは [Fe/H] = -1 付近である。 　したがって、もし観測球状星団のうち 47 Tuc だけが [Ca/Fe] = 0.0 で、他の 星団は [Ca/Fe] = 0.3 ならば、図４上で 47 Tuc （右端）の有効位置は 0.3 下がり、 (この議論は完全には明快ではない？) 直線性はよくなると思われる。今後 [Ca/Fe] と [Fe/H] の関係データがさらに 集まるとこの影響がはっきりするだろう。

図４．変換擬等値幅、(W8542 + W8662) + 0.619(V-VHB) と星団 [Fe/H] との関係。NGC 1851 は二つの [Fe/H] 、-1.16 と -1.29、 が報告されているので両方を載せた。フィットは 低メタルでは直線、高メタルでは３次式を用いて結合した。 直線部分は次の式で良くフィットする。 　[Fe/H] = 0.326 W' - 2.706 (図４には [Ca/Fe] の変化が含まれているから、応用に 際してはその天体の [Ca/Fe] が球状星団の変化と合致するか注意必要。)

　４．プログラム星団　

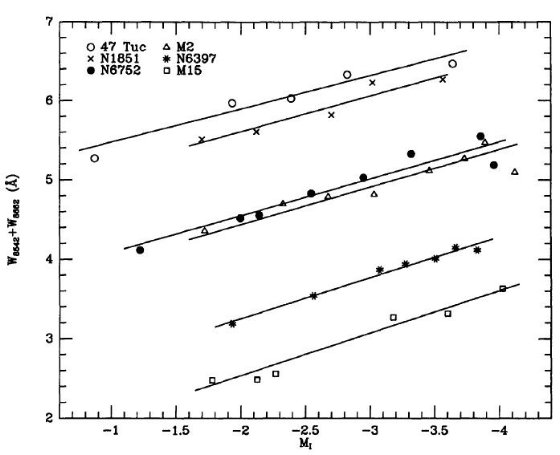
４．１．視線速度　 　Pal 12 　Pal 12 は平均 28.5±1.4 km/s で、速度巾は 5.6 km/s であった。この 狭い巾と位置から観測した星は全てメンバーと考えられる。上の速度巾は 観測誤差で説明できる値であり、速度分散は得られていない。 　エリダヌス　 　エリダヌスの二つの巨星は平均 -23.8 km/s, 差が 0.4 km/s であった。 この二つともメンバーであろう。 　カリーナ　 　５つの星を観測した。二つは視線速度からメンバーでないと考えられる。 　４．２．組成　 　４．２．１．エリダヌス　 　二つのエリダヌス星は図５上で NGC6752 と NGC1851 の間に来る。二つの星の 変換擬等値幅は、 W' = 4.11±0.28, 3.90±0.20 A である。 観測数で重みを付けた 平均値は W' = 3.97±0.13 A で、直線変換式から [Fe/H] = -1.41&plumn;0.04 （内部エラー）を得る。不定性は較正星団のメタル量の不定性による較正エラーを 考えるとエラーは 0.11 に上がる。このメタル量は DaCosta, Armandroff 1990 が (MI, (V-I)o)図上の巨星枝位置から出した [Fe/H] = -1.50$plusmn;0.15 と一致している。 　４．２．２．カリーナ　 　(B-V)og 法と CaT 法の不一致　 　カリーナは図５上、NGC6752 のすぐ近くに位置し、[Fe/H] = -1.52±0.13 を与える。Mighell 1990 は Mould,Aaronson 1983 の (B-V)og と Zinn,West 1984 の (B-V)og 対 [Fe/H] 関係を使って [Fe/H] = -1.75±0.2 を導いた。この差の原因として、単に我々の分光した巨星が カリーナの組成を反映していないためかも知れないが、カリーナ星の多数が若く、 (B-V)og 較正に使った球状星団が老齢であったためかも知れない。 　 (B-V)og 法の年齢効果　 この点を調べるため、イエール等時線を使い、 Z = 0.0004, Y = 0.2, t = 15 Gyr (球状星団)巨星枝と t = 7 Gyr(カリーナの大部分）巨星枝とで 7 Gyr の方が (B-V) で 0.026 青い事を見出した。したがって、カリーナの (B-V)og に球状星団で較正した [Fe/H] を使うと 0.1 低い値になる。この補正を加えると Mighell 1990 の [Fe/H] は我々の値にかなり近づく。 ( CaT の方には年齢効果の補正を加えないのはおかしい。) 　矮小銀河のメタル量・光度関係　 　興味深い事に、この新しい高メタル値は、銀河系矮小銀河で見られるメタル量と 絶対等級との間の相関(DaCosta 1988)を悪くする。例えば、カリーナの新しい メタル量は明るいスカルプターより 0.2 - 0.3 dex 大きく、最も明るいフォル ナックスのメタル量にくらべ僅かに小さいだけである。

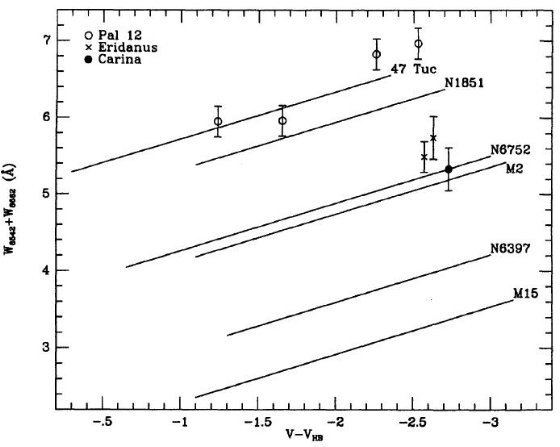
図５．図３の上にプログラム星団の観測結果を重ねた。 　４．２．３． Pal 12 　CaT 法と色等級図法の不一致　 　Pal 12 巨星は図５上で 47 Tuc の少し上にならび、かなり高メタルである ことを示唆する。変換擬等値幅は 5.24±0.12 A であり、較正曲線の 3 次式部分を使うと [Fe/H] = -0.60&plumn; -0.14 となる。この値は DaCosta,Armandroff 1990 が (MI, (V-I)o) 色等級図上の巨星位置 から導いた [Fe/H] = -1.06&plumn; -0.12 より大分大きい。 　 [Ca/Fe] の不定性　 　しかし、ここでの CaT 法は Pal 12 と 47 Tuc の [Ca/Fe] がほぼ同じという 仮定に頼っている。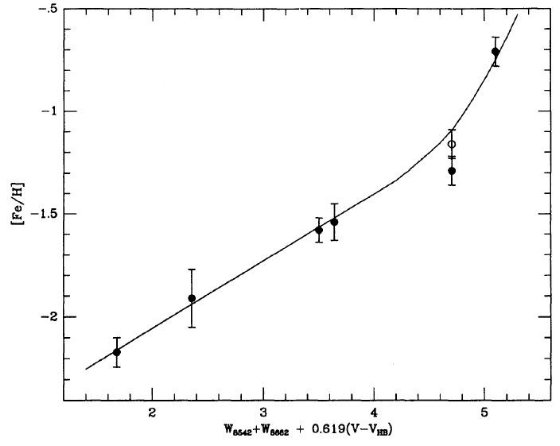実際もしも Pal 12 の [Ca/Fe] = +0.3 で 47 Tuc 以外の球状 星団と同じで、図４の直線フィット式をそのまま適用できるとすると、 [Fe/H] = -1.0±0.1 となり、色等級図法と極めて近くなる。このように [Fe/H] の場合には CaT 法の適用には [Ca/Fe] 効果への注意が必要である。 　分光と測光の差　 　面白い事に分光で出した [Fe/H] は系統的に測光法での値より大きい。 測光法 （１）Zinn,West は (B-V)og = 0.89 から [Fe/H] = -1.14±0.20 とした。 （２）Cohen et al 1980 は Pal 12 巨星枝が M71 と M3 の間に来ることから、 [Fe/H] = -0.94 を得た。 （３）DaCosta,Armandroff 1990 は (MI, (V-I)o) 色等級図上の巨星位置 から [Fe/H] = -1.06&plumn; -0.12 を導いた 分光法 （１）Cohen et al 1980 は 5200 A 付近で Mg, Ca, Cr, Fe ライン強度を測り、 Pal 12 メタル量が M5 より大きく、 M71 に近いとした。[Fe/H]M71 = -0.58 である。 （２）Bell 1984 は合成スペクトルのフィットを行い、CaI&lambda:4226 ラインから -0.8±0.1, CaII H, K 線から -0.9±0.2 を得た。 （３）今回の CaT 法は [Fe/H] = -0.60&plumn; -0.14 [Ca/Fe] が大きい可能性があると, 分光法で導いた値はその影響を受ける。 例えば、Bell のフィットは希釈太陽組成を仮定している。したがって、[Ca/Fe] が 正だとその分 [Fe/H] は影響を受ける。Cohen et al 1980 の分光について言うと、 彼らのライン強度指数への最大の貢献は 5170A の MgIb線から来ている。Mg は α 元素なので Ca と同様に低メタルのハロー星では増加が知られている。 したがって、 Pal 12 での測光メタル量と分光メタル量の違いは Pal 12 では [α/Fe] が 47 Tuc より大きいと考えると解消するのである。

　５．まとめ