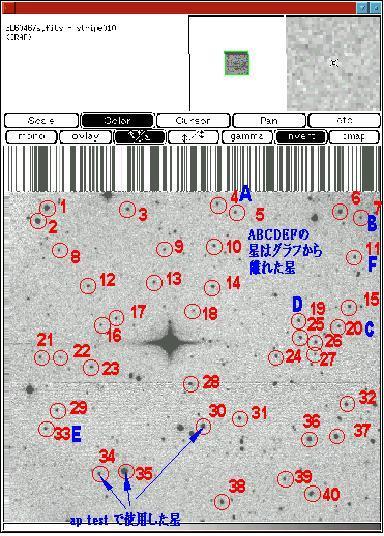
まず、1月と2月のデータからAPPHOTOで得られた等級をもとに作ったグラフを考察することから始める。
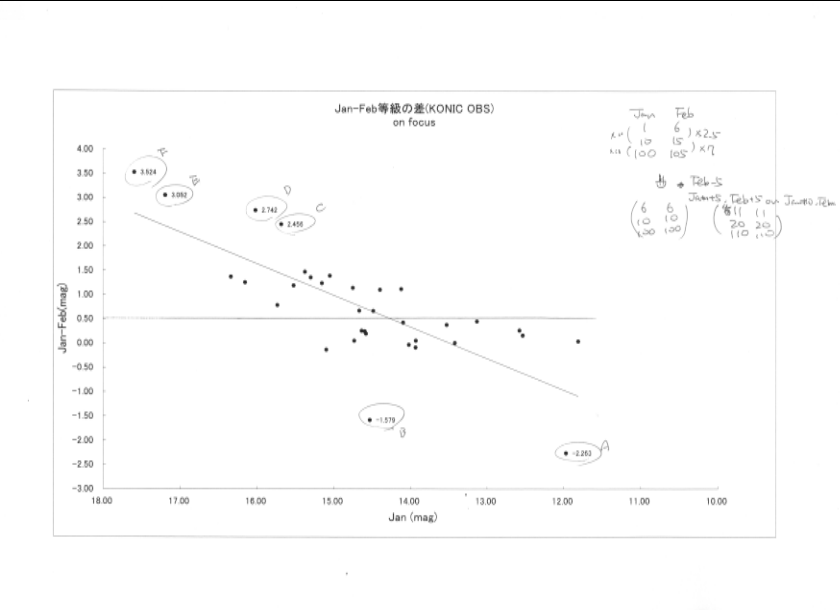

分散の大きいA-Fの6個の星(上の図参照)を除くと、最小2乗の直線は比較的水平になりそうなことがわかる。
これら6個の星は、等級比較のグラフでは以下のところにプロットされる。
これらの星は、他の星に対して特別な影響(画面のはしのケラレ、感度むら、ノイズなど)を受けた、
と考えるとして、とりあえず除外してみても、y=x、45度の直線からは、ずれて分布している傾向がみられる。
この傾きの変化は、1月と2月で、カウントにゲタがある影響と思われるので、そのゲタを補正を試みる。
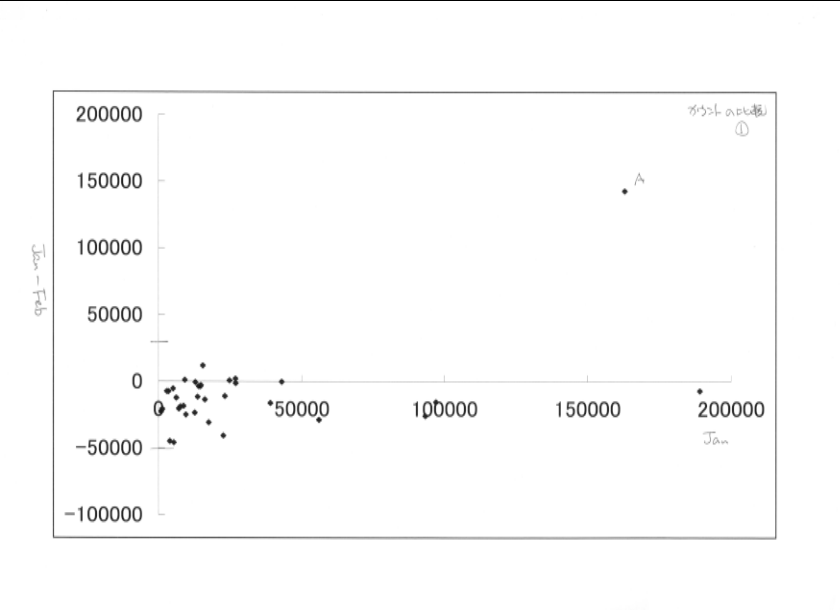
先の6個の星のうちA星は、右上の高いところに出ている。これは、何か特別な影響によるとみて、
その他の星でゲタを求める。
下図は、y=-20000付近を拡大してみたもの。
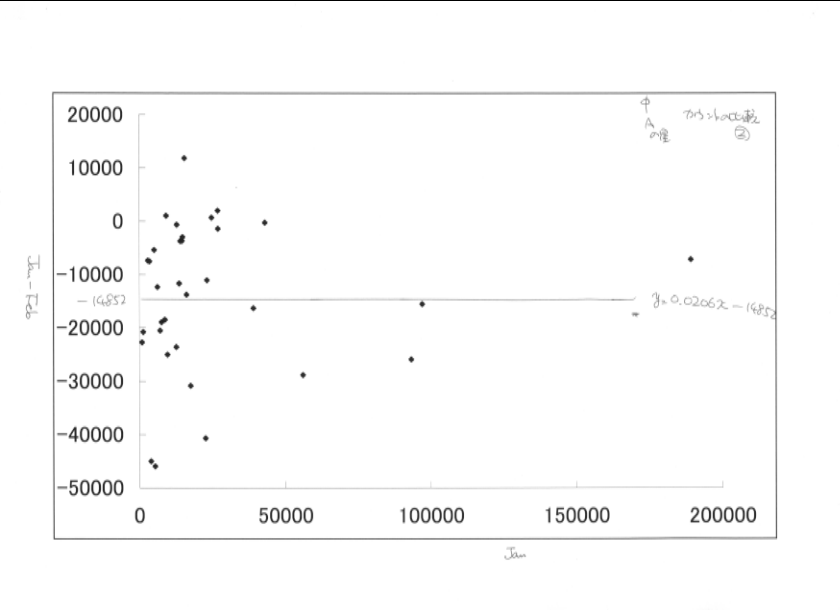
かなり水平に分布していることがわかる。
上図よりゲタの量は、-14852と求められる。
2月のカウントから、14852引く。
カウントがマイナスになってしまうものが出たため、2月のカウントに4000を加える。
同様に、1月のカウントにも4000加える。
(→はじめに、1月のカウントに14852足す方が方法はスマートだった。)
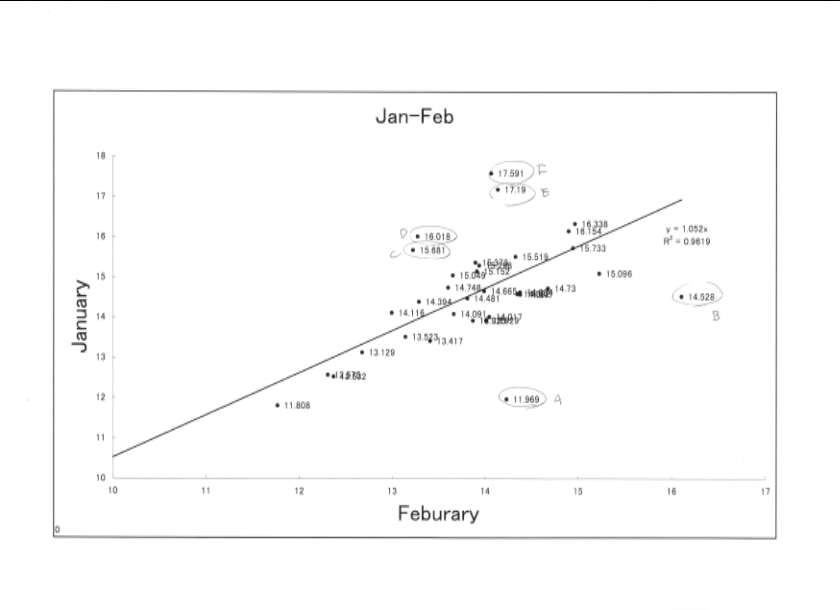
これらの値から、1月と2月の『インストゥルメンタルマグニチュード』を求める。
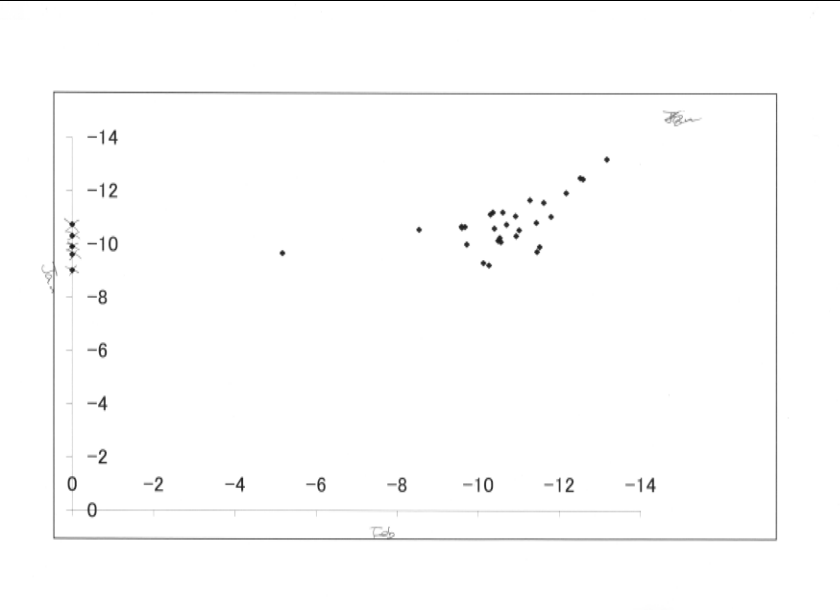
下図はその等級値を使って、1月と2月の等級を比較したもの。
きれいに45度の直線にならび、暗くなるにしたがって分散が大きくなっている様子が見られる。
Aの星も、ずっと左側に来ており、分散の大きいところにあることがわかる。
あとの5個の星も分散の大きいところに入っているものと思われる。
→要確認
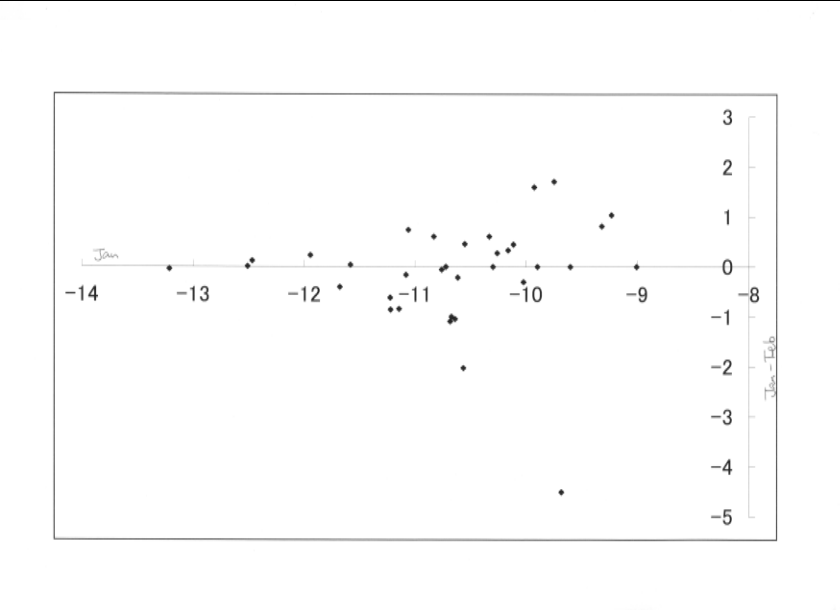
下図は、等級の差について調べたもの。
きれいに水平にならぶ。
まずは、カウントの差をなくす方法を確立すること。
図6は、ゲタの補正がきちんと行われれば、ある等級での観測の誤差は評価できる、ということを示している。
次に、オンフォーカスとオフフォーカスの問題をきちんと評価することが残されている。
それができれば、いよいよ、ミラ型星の変光観測の誤差を評価することができる(!?)。
変光観測の最初のページに戻る